ACM学习历程—HDU 5289 Assignment(线段树 || RMQ || 单调队列)

Problem Description

Tom owns a company and he is the boss. There are n staffs which are numbered from 1 to n in this company, and every staff has a ability. Now, Tom is going to assign a special task to some staffs who were in the same group. In a group, the difference of the ability of any two staff is less than k, and their numbers are continuous. Tom want to know the number of groups like this.

 

Input

In the first line a number T indicates the number of test cases. Then for each case the first line contain 2 numbers n, k (1<=n<=100000, 0<k<=10^9),indicate the company has n persons, k means the maximum difference between abilities of staff in a group is less than k. The second line contains n integers:a[1],a[2],…,a[n](0<=a[i]<=10^9),indicate the i-th staff’s ability.

 

Output

For each test，output the number of groups.

 

Sample Input

2 4 2 3 1 2 4 10 5 0 3 4 5 2 1 6 7 8 9

 

Sample Output

5 28

Hint

First Sample, the satisfied groups include:[1,1]、[2,2]、[3,3]、[4,4] 、[2,3]

题目大意是求满足下列条件的子区间的个数：

对于子区间[L, R]内的任意两个元素的差值小于k。

大概有以下三种方法：

第一种：（线段树）

首先可以肯定的是，以An起始的区间肯定是[n, n]。

然后以An-1起始的区间最长是[n-1, n]，然后考虑需不需要把区间的右值减小，也就是考虑An和An-1的差值是否小于k。假设最终的区间为[n-1, d(n-1)]。

于是对于以An-2起始的区间，自然最长是[n-2, d(n-1)]，然后考虑需不需要把区间的右值减小，也就是考虑这个区间内是否存在某个值与An-2的差值大于等于k。

以此类推，以Ai起始的区间应为[i, min(d(i+1), p)]，其中p是i右侧最后一个满足与Ai差值小于k的数的脚标。

于是采用线段树记录区间的最大值和最小值，就能查询出任意[i, n]区间里第一个满足与Ai差值大于等于k的值的位置x，然后x-1即为最后一个满足与Ai差值小于k的数的脚标。

（此处采用ans记录x，ans为-1表示没找到，自然x-1就是n）

复杂度：n*logn（枚举左端点*查询右端点）

代码：（线段树）

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <set>
#include <map>
#include <queue>
#include <string>
#include <algorithm>
#define LL long long

using namespace std;

int n, k;
int a[], ans;
int d[];

//线段树
//区间每点增值，求区间和
const int maxn = ;
struct node
{
    int lt, rt;
    LL mi, ma;
}tree[*maxn];

//向上更新
void pushUp(int id)
{
    tree[id].mi = min(tree[id<<].mi, tree[id<<|].mi);
    tree[id].ma = max(tree[id<<].ma, tree[id<<|].ma);
}

//建立线段树
void build(int lt, int rt, int id)
{
    tree[id].lt = lt;
    tree[id].rt = rt;
    tree[id].mi = ;//每段的初值，根据题目要求
    tree[id].ma = ;
    if (lt == rt)
    {
        tree[id].mi = tree[id].ma = a[lt];
        return;
    }
    int mid = (lt + rt) >> ;
    build(lt, mid, id<<);
    build(mid+, rt, id<<|);
    pushUp(id);
}

void query(int lt, int rt, int id, int v)
{
    if (tree[id].lt == tree[id].rt)
    {

        if (abs(tree[id].mi-v) >= k)
        {
            if (ans == - || ans > tree[id].lt)
                ans = tree[id].lt;
        }
        return;
    }
    int mid = (tree[id].lt + tree[id].rt) >> ;
    if (lt <= mid)
        if (abs(tree[id<<].mi-v) >= k || abs(tree[id<<].ma-v) >= k)
            query(lt, rt, id<<, v);
    if (ans == - && rt > mid)
        if (abs(tree[id<<|].mi-v) >= k || abs(tree[id<<|].ma-v) >= k)
            query(lt, rt, id<<|, v);
}

void input()
{
    scanf("%d%d", &n, &k);
    for (int i = ; i <= n; ++i)
    {
        scanf("%d", &a[i]);
    }
    build(, n, );
}

void work()
{
    LL sum = ;
    d[n] = n;
    for (int i = n-; i >= ; --i)
    {
        ans = -;
        query(i, n, , a[i]);
        if (ans != -)
            ans -= ;
        else
            ans = n;

        d[i] = min(ans, d[i+]);
        sum += d[i]-i+;
    }
    printf("%lld\n", sum);
}

int main()
{
    //freopen("test.txt", "r", stdin);
    int T;
    scanf("%d", &T);
    for (int times = ; times < T; ++times)
    {
        input();
        work();
    }
    return ;
}

第二种：（RMQ+二分区间长度）

使用RMQ可以对于无修改操作的任意区间的最值进行查询。

这样就可以枚左端点，然后二分区间长度得到右端点（此处直接二分了右端点的位置）。

第一次使用RMQ，一个小错误找了很久。

当然此处仍可以用线段树维护最值，但是效率有损。

复杂度：n*logn*logn（枚举左端点*二分右端点*RMQ查询时得到的区间长度的log）

代码：（RMQ）

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <set>
#include <map>
#include <string>
#include <queue>
#include <vector>
#define LL long long

using namespace std;

const int maxN = ;

int n, k;
int a[maxN];
int mi[maxN][], ma[maxN][];

void RMQ()
{
    for (int i = ; i < n; ++i)
        mi[i][] = ma[i][] = a[i];
    for (int j = ; (<<j) <= n; ++j)
        for (int i = ; i+(<<j)- < n; ++i)
        {
            mi[i][j] = min(mi[i][j-], mi[i+(<<(j-))][j-]);
            ma[i][j] = max(ma[i][j-], ma[i+(<<(j-))][j-]);
        }

}

int query(int lt, int rt)
{
    int k = ;
    while ((<<(k+)) <= rt-lt+)
        k++;
    return max(ma[lt][k], ma[rt-(<<k)+][k]) - min(mi[lt][k], mi[rt-(<<k)+][k]);
}

int binarySearch(int from)
{
    int lt = from, rt = n-, mid;
    while (lt+ < rt)
    {
        mid = (lt+rt)>>;
        if (query(from, mid) >= k)
            rt = mid;
        else
            lt = mid;
    }
    if (query(from, rt) < k)
        return rt;
    else
        return lt;
}

void input()
{
    scanf("%d%d", &n, &k);
    for (int i = ; i < n; ++i)
        scanf("%d", &a[i]);
    RMQ();
}

void work()
{
    LL ans = ;
    int to;
    for (int i = ; i < n; ++i)
    {
        to = binarySearch(i);
        ans += to-i+;
    }
    printf("%lld\n", ans);
}

int main()
{
    //freopen("test.in", "r", stdin);
    int T;
    scanf("%d", &T);
    for (int times = ; times < T; ++times)
    {
        input();
        work();
    }
    return ;
}

第三种：（单调队列）

这个问题由于之前线段树是枚举左端点，然后找最大的满足条件的右端点，即右侧首个不满足条件的点的左侧一个点。

重点是左端点是从大到小取的。这样才能保证左端点变小以后，其不包含左端点的子区间也能满足要求。显然，不包含当前左端点的子区间就是上一次满足条件的最大区间的子区间。

如果从小到大取左端点。那么必然新增的点都在右端，然而并不能保证这右边新增的点与原来的点满足条件。

可以对左端点枚举的话，同理可以对右端点枚举。这里为了看起来方便一点，就对枚举右端点的情况进行考虑。

自然思路还是一样的，枚举右端点，然后找满足条件的最小的右端点，自然跟线段树的做法一样，是考虑上一次满足条件的区间，加入新的右端点后考虑需要排掉多少左端的点。

到这里就是需要维护当前区间最值，可以使用两个优先队列一个维护当前队列的最小值，一个维护最大值；然后对于一个队列，把在区间外的值直接弹出容器，然后把不满足条件的值弹出容器，维护弹出的脚标的最大值。然后优先队列取出来的值取较大的。

这样的话效率是nlogn。但是会发现，对于区间外的值其实好多是没必要进队列的。而且对于一个这样的数列，如图

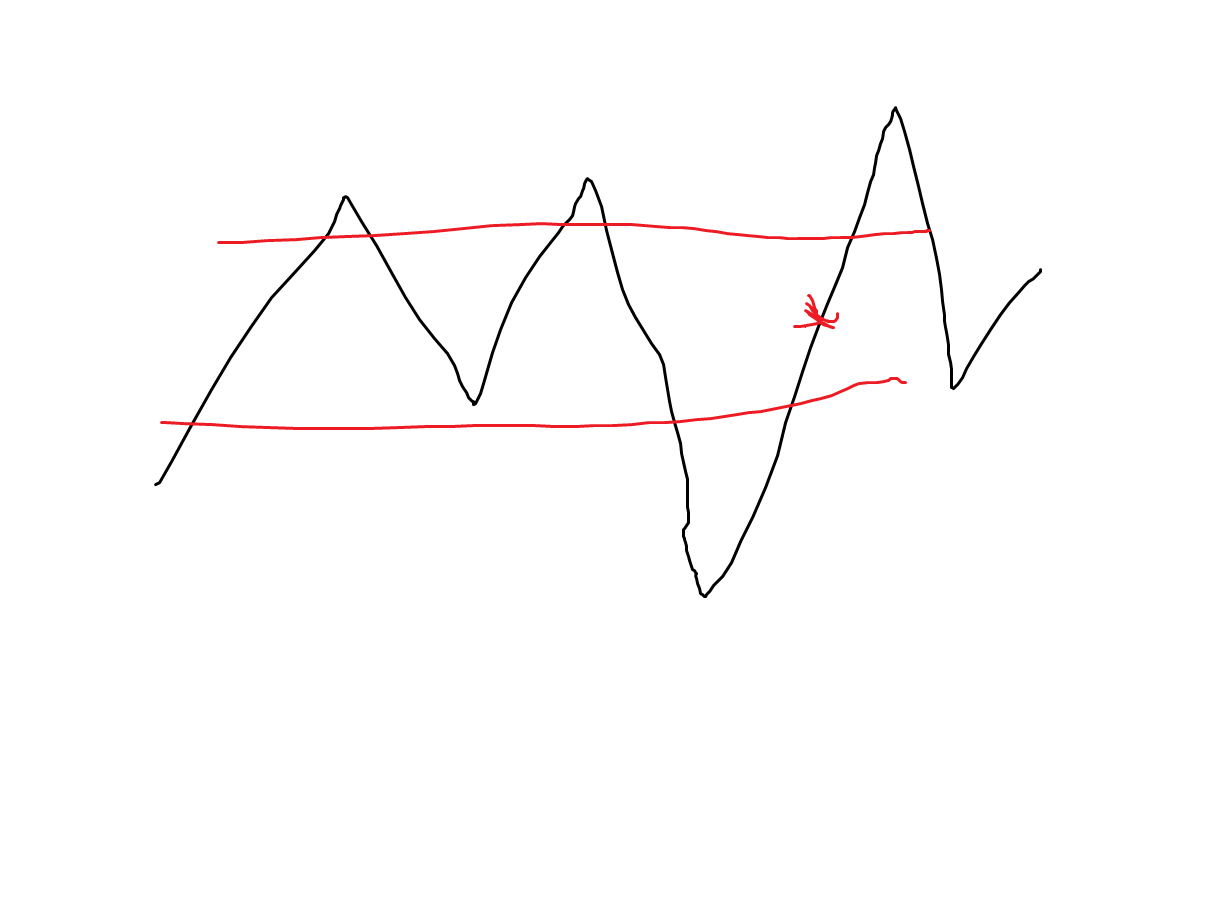
对于某个右端点来说，对于它前面上下波动k范围内的点，左端点肯定是取从左往右最后一个不满足条件的的右边一个点（当都满足取第一个）。

这样对于某两个不满足条件的点中间的一些满足条件的点自然是不需要进队的。

此外就是可以显而易见的，前一个区间加入新的右端点后，左端点只会向右移动或者不动，有了这个前提就可以实施上述方案了。

然后就可以维护两个单调的队列，一个是递增的，一个是递减的。即一个维护上界，一个维护下届的。

这样就和线段树一样，判断上界和下界是否和a[i]差值大于等于k，否则需要把区间缩小。（这里需要注意的是两个队列只有一开始是空的，后面至少有一个元素）

然后就是维护单调性：

对于递增的那个队列来说，当新的右端点加入后，如果右端点大于队列里面所有的数，自然直接进队，如果小于队列末端的点就弹出右端的点直到满足第一个条件。递减的类似。这样对于递增的队列来说，两个低点中间的高点没有进队列。对于递减队列来说，两个高点中间的低点没有进队列.

这样每个元素最多进一次队列，整体效率是O(n)的。

代码：(单调队列)

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cmath>
#include <cstring>
#include <set>
#include <map>
#include <deque>
#include <vector>
#include <string>
#include <utility>
#include <algorithm>
#define LL long long

using namespace std;

const int maxN = ;
int n, k, a[maxN];
LL ans;

void input()
{
    scanf("%d%d", &n, &k);
    for (int i = ; i < n; ++i)
        scanf("%d", &a[i]);
}

void work()
{
    if (k == )
    {
        printf("0\n");
        return;
    }
    ans = ;
    deque<int> mi, ma;
    int p = ;
    for (int i = ; i < n; ++i)
    {
        while (!(mi.empty() && ma.empty()) &&
               !(abs(a[i]-a[mi.front()]) < k && abs(a[i]-a[ma.front()]) < k))
        {
            p++;
            while (!mi.empty() && mi.front() < p)
                mi.pop_front();
            while (!ma.empty() && ma.front() < p)
                ma.pop_front();
        }
        ans += i-p+;
        while (!mi.empty() && a[mi.back()] > a[i])
            mi.pop_back();
        mi.push_back(i);
        while (!ma.empty() && a[ma.back()] < a[i])
            ma.pop_back();
        ma.push_back(i);
    }
    printf("%lld\n", ans);
}

int main()
{
    //freopen("test.in", "r", stdin);
    int T;
    scanf("%d", &T);
    for (int times = ; times < T; ++times)
    {
        input();
        work();
    }
    return ;
}