Leetcode 446.等差数列划分II 子序列

等差数列划分II 子序列

如果一个数列至少有三个元素，并且任意两个相邻元素之差相同，则称该数列为等差数列。

例如，以下数列为等差数列:

1, 3, 5, 7, 9

7, 7, 7, 7

3, -1, -5, -9

以下数列不是等差数列。

1, 1, 2, 5, 7

数组 A 包含 N 个数，且索引从 0 开始。该数组子序列将划分为整数序列 (P₀, P₁, ..., P_k)，P 与 Q 是整数且满足 0 ≤ P₀ < P₁ < ... < P_k < N。

如果序列 A[P₀]，A[P₁]，...，A[P_k-1]，A[P_k] 是等差的，那么数组 A 的子序列 (P0，P1，…，PK) 称为等差序列。值得注意的是，这意味着 k ≥ 2。

函数要返回数组 A 中所有等差子序列的个数。

输入包含 N 个整数。每个整数都在 -2³¹ 和 2³¹-1 之间，另外 0 ≤ N ≤ 1000。保证输出小于 2³¹-1。

示例：

输入：[2, 4, 6, 8, 10]

输出：7

解释：

所有的等差子序列为：

[2,4,6]

[4,6,8]

[6,8,10]

[2,4,6,8]

[4,6,8,10]

[2,4,6,8,10]

[2,6,10]

Dynamic Programming [Accepted]

Intuition

To determine an arithmetic sequence, we need at least two parameters: the first (or last) element of the sequence, and the common difference.

Algorithm

Starting from this point, we can easily figure out that one state representation that may work:

f[i][d] denotes the number of arithmetic subsequences that ends with A[i] and its common difference is d.

Let's try to find the state transitions based on the representation above. Assume we want to append a new element A[i] to existing arithmetic subsequences to form new subsequences. We can append A[i] to an existing arithmetic subsequence, only if the difference between the sequence's last element and A[i] is equal to the sequence's common difference.

Thus, we can define the state transitions for the element A[i] intuitively :

for all j < i, f[i][A[i] - A[j]] += f[j][A[i] - A[j]].

This demonstrates the appending process above to form new arithmetic subsequences.

But here comes the problem. Initially all f[i][d] are set to be 0, but how can we form a new arithmetic subsequence if there are no existing subsequences before?

In the original definition of arithmetic subsequences, the length of the subsequence must be at least 3. This makes it hard to form new subsequences if only two indices i and j are given. How about taking the subsequences of length 2 into account?

We can define weak arithmetic subsequences as follows:

Weak arithmetic subsequences are subsequences that consist of at least two elements and if the difference between any two consecutive elements is the same.

There are two properties of weak arithmetic subsequences that are very useful:

• For any pair i, j (i != j), A[i] and A[j] can always form a weak arithmetic subsequence.
• If we can append a new element to a weak arithmetic subsequence and keep it arithmetic, then the new subsequence must be an arithmetic subsequence.

The second property is quite trival, because the only difference between arithmetic subsequences and weak arithmetic subsequences is their length.

Thus we can change the state representations accordingly:

f[i][d] denotes the number of weak arithmetic subsequences that ends with A[i] and its common difference is d.

Now the state transitions are quite straightforward:

for all j < i, f[i][A[i] - A[j]] += (f[j][A[i] - A[j]] + 1).

The 1 appears here because of the property one, we can form a new weak arithmetic subsequence for the pair (i, j).

Now the number of all weak arithmetic subsequences is the sum of all f[i][d]. But how can we get the number of arithmetic subsequences that are not weak?

There are two ways:

• First, we can count the number of pure weak arithmetic subsequences directly. The pure weak arithmetic subsequences are the arithmetic subsequences of length 2, so the number of pure weak arithmetic subsequences should be equal to the number of pairs (i, j), which is (n2)=n∗(n−1)2.\binom{n}{2} = \frac{n * (n - 1)}{2}.(2n​)=2n∗(n−1)​.
• Second, for the summation f[i][A[i] - A[j]] += (f[j][A[i] - A[j]] + 1), f[j][A[i] - A[j]] is the number of existing weak arithmetic subsequences, while 1 is the new subsequence built with A[i] and A[j]. Based on property two, when we are appending new elements to existing weak arithmetic subsequences, we are forming arithmetic subsequences. So the first part, f[j][A[i] - A[j]] is the number of new formed arithmetic subsequences, and can be added to the answer.

We can use the following example to illustrate the process:

[1, 1, 2, 3, 4, 5]

We need to count the answer for the above sequence.

• For the first element 1, there is no element in front of it, the answer remains 0.
• For the second element 1, the element itself with the previous 1 can form a pure weak arithmetic subsequence with common difference 0 : [1, 1].
• For the third element 2, it cannot be appended to the only weak arithmetic subsequence [1, 1], so the answer remains 0. Similar to the second element, it can form new weak arithmetic subsequences [1, 2] and [1, 2].
• For the forth element 3, if we append it to some arithmetic subsequences ending with 2, these subsequences must have a common difference of 3 - 2 = 1. Indeed there are two: [1, 2] and [1, 2]. So we can append 3 to the end of these subsequences, and the answer is added by 2. Similar to above, it can form new weak arithmetic subsequences [1, 3], [1, 3] and [2, 3].
• The other elements are the same, we can view the process in the figure below. The red bracket indicates the weak arithmetic subsequence of length 2, and the black bracket indicates the arithmetic subsequence. The answer should be the total number of black brackets.

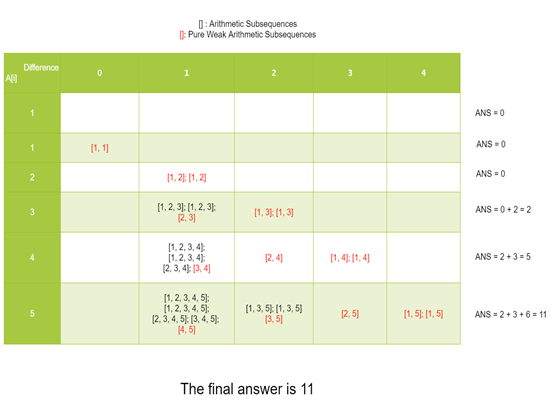
 class Solution {
     public int numberOfArithmeticSlices(int[] A) {
         int n = A.length;
         long ans = 0;
         Map<Integer, Integer>[] cnt = new Map[n];
         for (int i = 0; i < n; i++) {
             cnt[i] = new HashMap<>(i);
             for (int j = 0; j < i; j++) {
                 long delta = (long)A[i] - (long)A[j];
                 if (delta < Integer.MIN_VALUE || delta > Integer.MAX_VALUE) {
                     continue;
                 }
                 int diff = (int)delta;
                 int sum = cnt[j].getOrDefault(diff, 0);
                 int origin = cnt[i].getOrDefault(diff, 0);
                 cnt[i].put(diff, origin + sum + 1);
                 ans += sum;
             }
         }
         return (int)ans;
     }
 }