Python数据结构—

数的特征和定义：

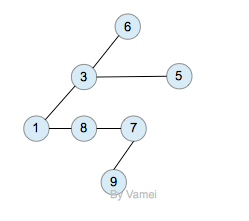
树是一种重要的非线性数据结构，直观地看，它是数据元素（在树中称为结点）按分支关系组织起来的结构，很象自然界中的树那样。树结构在客观世界中广泛存在，如人类社会的族谱和各种社会组织机构都可用树形象表示。树在计算机领域中也得到广泛应用，如在编译源程序时，可用树表示源程序的语法结构。又如在数据库系统中，树型结构也是信息的重要组织形式之一。一切具有层次关系的问题都可用树来描述。

树(Tree)是元素的集合。我们先以比较直观的方式介绍树。下面的数据结构是一个树：

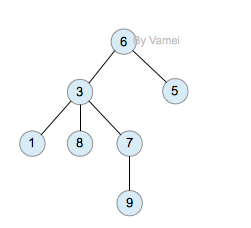
树有多个节点(node)，用以储存元素。某些节点之间存在一定的关系，用连线表示，连线称为边(edge)。边的上端节点称为父节点，下端称为子节点。树像是一个不断分叉的树根。

每个节点可以有多个子节点(children)，而该节点是相应子节点的父节点(parent)。比如说，3,5是6的子节点，6是3,5的父节点；1,8,7是3的子节点, 3是1,8,7的父节点。树有一个没有父节点的节点，称为根节点(root)，如图中的6。没有子节点的节点称为叶节点(leaf)，比如图中的1,8,9,5节点。从图中还可以看到，上面的树总共有4个层次，6位于第一层，9位于第四层。树中节点的最大层次被称为深度。也就是说，该树的深度(depth)为4。

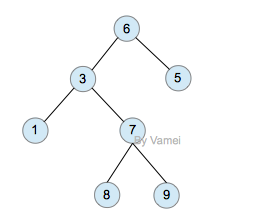
如果我们从节点3开始向下看，而忽略其它部分。那么我们看到的是一个以节点3为根节点的树：

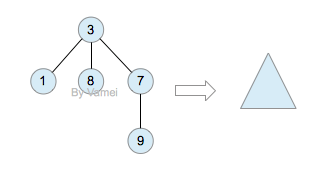
三角形代表一棵树

再进一步，如果我们定义孤立的一个节点也是一棵树的话，原来的树就可以表示为根节点和子树(subtree)的关系:

上述观察实际上给了我们一种严格的定义树的方法：

1. 树是元素的集合。

2. 该集合可以为空。这时树中没有元素，我们称树为空树 (empty tree)。

3. 如果该集合不为空，那么该集合有一个根节点，以及0个或者多个子树。根节点与它的子树的根节点用一个边(edge)相连。

上面的第三点是以递归的方式来定义树，也就是在定义树的过程中使用了树自身(子树)。由于树的递归特征，许多树相关的操作也可以方便的使用递归实现。我们将在后面看到。

数的实现

树的示意图已经给出了树的一种内存实现方式: 每个节点储存元素和多个指向子节点的指针。然而，子节点数目是不确定的。一个父节点可能有大量的子节点，而另一个父节点可能只有一个子节点，而树的增删节点操作会让子节点的数目发生进一步的变化。这种不确定性就可能带来大量的内存相关操作，并且容易造成内存的浪费。

一种经典的实现方式如下:

树的内存实现

拥有同一父节点的两个节点互为兄弟节点(sibling)。上图的实现方式中，每个节点包含有一个指针指向第一个子节点，并有另一个指针指向它的下一个兄弟节点。这样，我们就可以用统一的、确定的结构来表示每个节点。

计算机的文件系统是树的结构，比如Linux文件管理背景知识中所介绍的。在UNIX的文件系统中，每个文件(文件夹同样是一种文件)，都可以看做是一个节点。非文件夹的文件被储存在叶节点。文件夹中有指向父节点和子节点的指针(在UNIX中，文件夹还包含一个指向自身的指针，这与我们上面见到的树有所区别)。在git中，也有类似的树状结构，用以表达整个文件系统的版本变化 (参考版本管理三国志)。

二叉树：　

二叉树是由n（n≥0）个结点组成的有限集合、每个结点最多有两个子树的有序树。它或者是空集，或者是由一个根和称为左、右子树的两个不相交的二叉树组成。

特点：

（1）二叉树是有序树，即使只有一个子树，也必须区分左、右子树；

（2）二叉树的每个结点的度不能大于2，只能取0、1、2三者之一；

（3）二叉树中所有结点的形态有5种：空结点、无左右子树的结点、只有左子树的结点、只有右子树的结点和具有左右子树的结点。

二叉树(binary)是一种特殊的树。二叉树的每个节点最多只能有2个子节点：

二叉树

由于二叉树的子节点数目确定，所以可以直接采用上图方式在内存中实现。每个节点有一个左子节点(left children)和右子节点(right children)。左子节点是左子树的根节点，右子节点是右子树的根节点。

如果我们给二叉树加一个额外的条件，就可以得到一种被称作二叉搜索树(binary search tree)的特殊二叉树。二叉搜索树要求：每个节点都不比它左子树的任意元素小，而且不比它的右子树的任意元素大。

(如果我们假设树中没有重复的元素，那么上述要求可以写成：每个节点比它左子树的任意节点大，而且比它右子树的任意节点小)

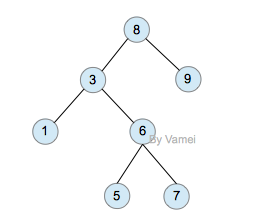
二叉搜索树，注意树中元素的大小

二叉搜索树可以方便的实现搜索算法。在搜索元素x的时候，我们可以将x和根节点比较:

1. 如果x等于根节点，那么找到x，停止搜索 (终止条件)

2. 如果x小于根节点，那么搜索左子树

3. 如果x大于根节点，那么搜索右子树

二叉搜索树所需要进行的操作次数最多与树的深度相等。n个节点的二叉搜索树的深度最多为n，最少为log(n)。

二叉树的遍历

遍历即将树的所有结点访问且仅访问一次。按照根节点位置的不同分为前序遍历，中序遍历，后序遍历。

前序遍历：根节点->左子树->右子树

中序遍历：左子树->根节点->右子树

后序遍历：左子树->右子树->根节点

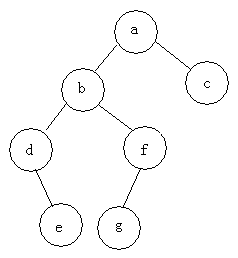
例如：求下面树的三种遍历

前序遍历：abdefgc

中序遍历：debgfac

后序遍历：edgfbca

二叉树的类型

(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

(3)平衡二叉树——平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树

如何判断一棵树是完全二叉树？按照定义，

教材上的说法：一个深度为k，节点个数为 2^k - 1 的二叉树为满二叉树。这个概念很好理解，

就是一棵树，深度为k，并且没有空位。

首先对满二叉树按照广度优先遍历（从左到右）的顺序进行编号。

一颗深度为k二叉树，有n个节点，然后，也对这棵树进行编号，如果所有的编号都和满二叉树对应，那么这棵树是完全二叉树。

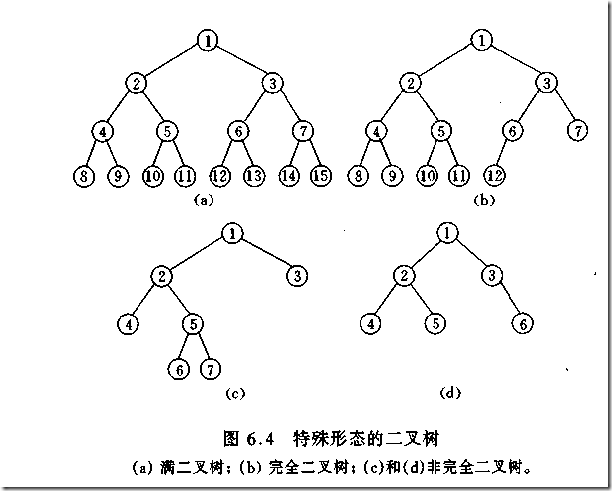
如何判断平衡二叉树？

（b）左边的图左子数的高度为3，右子树的高度为1，相差超过1

（b）右边的图 -2的左子树高度为0 右子树的高度为2，相差超过1

二叉树的遍历实现：

1、通过嵌套列表实现

 def binary_tree(r):

     return [r,[],[]]

 def insert_left(root,new_branch):

     t = root.pop(1)

     if len(t) > 1:

         root.insert(1,[new_branch,t,[]])

     else:

         root.insert(1,[new_branch,[],[]])

     return root

 def insert_right(root,new_branch):

     t = root.pop(2)

     if len(t) > 1:

         root.insert(2,[new_branch,[],t])

     else:

         root.insert(2,[new_branch,[],[]])

     return root

 def get_root_val(root):

     return root[0]

 def set_root_val(root,new_val):

     root[0] = new_val

 def get_left_child(root):

     return root[1]

 def get_right_child(root):

     return root[2]

 r = binary_tree(3)

 insert_left(r,4)

 insert_left(r,5)

 insert_right(r,6)

 insert_right(r,7)

 l= get_left_child(r)

 print(l)

 set_root_val(l,9)

 print(r)

 insert_left(l,11)

 print(r)

 print(get_right_child(get_right_child(r)))

 # [5, [4, [], []], []]

 # [3, [9, [4, [], []], []], [7, [], [6, [], []]]]

 # [3, [9, [11, [4, [], []], []], []], [7, [], [6, [], []]]]

 # [6, [], []]

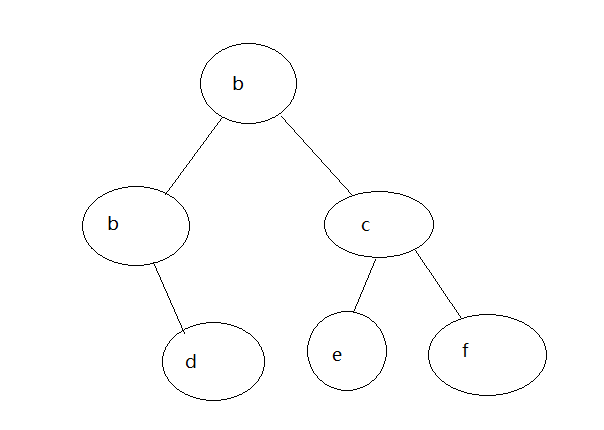
想要生成上图所示的数，代码如下：

x = binary_tree('a')

insert_left(x,'b')

insert_right(x,'c')

print(x)

insert_right(get_left_child(x),'d')

insert_left(get_right_child(x),'e')

insert_right(get_right_child(x),'f')

print(x)

#['a', ['b', [], []], ['c', [], []]]

#['a', ['b', [], ['d', [], []]], ['c', ['e', [], []], ['f', [], []]]]