[LeetCode] questions conclusion_ Binary Search

Binary Search

T(n) = T(n/2) + O(1)   =>    T(n) = O(lg n)

proof:

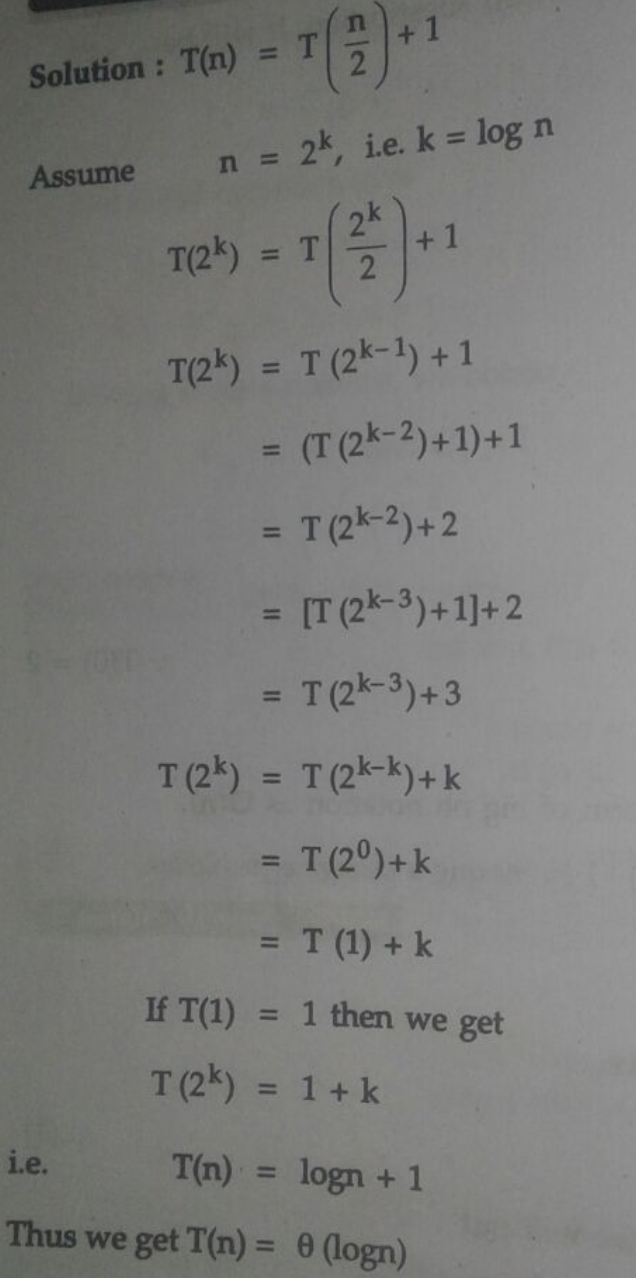
如果能用iterable , 就用while loop, 可以防止用recursion的时候stack overflow( process in Linux is 8Mb), stack room is static for each process. （堆空间， heap room 是内存， 是动态的。）层数越多，存储更多中间/临时变量，最终超过系统配的stack空间，就会出现stack overflow。

建议：

　　- 如果问题不复杂，能用iterable就用iterable

　　  - 如果问题比较复杂，还是用recursive吧

1) ask 是否有duplicates?

　　1.1  如果没有duplicates

　　标准的binary search:

　　a) l + 1 < r   相当于如果l, r 相邻就跳出，这样能够避免死循环. 但是while loop之后需要加一个判断, 也就是d选项

　　b) l + (r - l)//2      # 不用(l+r)//2 , 因为l + r 有可能overflow，强行装*，当l + r 之和超过int的最大值，2的32次方减1，会溢出。

　　c) A[mid] ==, <, >    # 为了bug free, 建议举个小栗子, 然后画图去判断.

　　d) A[l], A[r] ? target

　　Code

　　

def BinarySearch(self, nums, target):  # nums is sorted
    if not nums or target < nums[0] or target > nums[-1]: return -1
    l, r = 0, len(nums) -1  # note here is len(nums) -1
    while l + 1 < r:
        mid = l + (r - l)//2
        if nums[mid] > target:
            r = mid
        elif nums[mid] < target:
            l = mid
        else:
            return mid
    if nums[l] == target:
        return l
    if nums[r] == target:
        return r
    return -1

　　1.2 如果有duplicates

　　a) ask 是first index, last index or dont matter?

　　　　如果是first index:

　　　　　　if A[mid] == target: r = mid

　　　　　　最后判断 A[l] 和A[r] 的时候先判断 A[l]

　　　　如果是last index:　　

　　　　　　if A[mid] == target: l = mid

　　　　　　最后判断 A[l] 和A[r] 的时候先判断 A[r]

Questions:

[LeetCode] 704. Binary Search_Easy tag: Binary Search

[LeetCode] 374. Guess Number Higher or Lower_Easy tag: Binary Search 　　

[LeetCode] 34. Find First and Last Position of Element in Sorted Array == [LintCode] 61. Search for a Range_Easy tag: Binary Search 　　first index and last index  == target in duplicates.

[LeetCode] 35. Search Insert Position_Easy tag: Binary Search     first index >= target, without duplicates

[LeetCode] 278. First Bad Version_Easy tag: Binary Search      first index, without duplicates

[LeetCode] 162. Find Peak Element(852. Peak Index in a Mountain Array)_Medium tag: Binary Search

[LeetCode] 74. Search a 2D Matrix_Medium tag: Binary Search

[LeetCode] 240. Search a 2D Matrix II_Medium tag: Binary Search

[LeetCode] 69. Sqrt(x)_Easy tag: Binary Search

[LeetCode] 153. Find Minimum in Rotated Sorted Array_Medium tag: Binary Search   first index <= nums[-1]

[LeetCode] 154. Find Minimum in Rotated Sorted Array II_Hard tag: not real binary search anymore

 

[LeetCode] 33. Search in Rotated Sorted Array_Medium tag: Binary Search

[LeetCode] 81. Search in Rotated Sorted Array II_Medium tag: not real binary search anymore

[LeetCode] 702. Search in a Sorted Array of Unknown Size_Medium tag: Binary Search

[LeetCode] 4. Median of Two Sorted Arrays_Hard tag: Array, Binary Search