POJ 1064 1759 3484 3061 (二分搜索)

POJ 1064

题意

有N条绳子，它们长度分别为Li。如果从它们中切割出K条长度相同的绳子的话，这K条绳子每条最长能有多长？答案保留小数点后2位。

思路

二分搜索。这里要注意精度问题，代码中有详细说明；还有printf的%.2f会四舍五入的，需要*100再取整以截取小数点后两位。

#include<stdio.h>
#include<string.h>
#include<string>
#include<iostream>
#include<math.h>
#include<algorithm>
using namespace std;

int N, K;
double length[10000 + 5];
const double EPS = 1e-6; // EPS取得太小会死循环
bool C(double x) {
	int count = 0;
	for (int i = 0; i < N; ++i) count += int(length[i] / x);
	if (count >= K) return true;
	return false;
}
void solve() {
	double lb = 0.0, ub = 100000000.0;
	// while(ub - lb > EPS) { // 精度不好控制
	for (int i = 0; i < 100; ++i) { // 精度(1/2)^100=10e-30，lb几乎等于ub
		double mid = (lb + ub) / 2.0;
		if (C(mid)) lb = mid; // 半闭半开区间[lb, ub)
		else ub = mid;
	}
	printf("%.2f\n", floor(lb * 100) / 100); // .2f会四舍五入所以要先*100取整以截取
}
int main()
{
	scanf("%d%d", &N, &K);
	for (int i = 0; i < N; ++i) scanf("%lf", &length[i]);
	solve();
	return 0;
}

POJ 1759

题意

在New Year garland的地方需要挂灯笼，现已知最左边的灯笼高度H1=A和灯笼总数N，第i个灯笼高度满足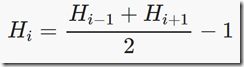，问最右边的灯笼HN能有多低（要求所有灯笼不着地）？

思路

后来确定第二个灯笼高度，即可确定第三个灯笼高度，以此类推，得到方程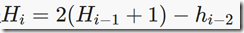，在用个数组标记下值，二分搜索出第二个灯笼最低高度，那么最后一个灯笼高度就是答案。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
int N;
double A;
double H[1005];
const double eps = 1e-6;
double h(int i, double x) { // 已知h(2) = x
	if (i == 1) return H[1] = A;
	else if (i == 2) return H[2] = x;
	else return H[i] = 2.0*H[i - 1] - H[i - 2] + 2.0;
}
bool C(double x) { // 判断第二个灯笼的高度为x，是否合适。
	for (int i = 1; i <= N; ++i)
	if (h(i, x) < eps) return false; // 一旦灯笼着地，即不符合要求
	return true;
}
void solve() {
	double lb = 0, ub = 10000.0;
	for (int i = 0; i < 100; ++i) { // 二分求出第二个灯笼到底该多低
		double mid = (ub + lb) / 2.0;
		if (C(mid)) ub = mid; // (lb, ub]
		else lb = mid;
	}
	printf("%.2f\n", H[N]); // 最后一个灯笼的高度
}
int main() {
	cin >> N >> A;
	solve();
	return 0;
}

POJ 3484

题意
给出一系列数据Xi,Yi,Zi表示序列Xi,Xi+Zi,⋯,Xi+K×Zi,⋯((Xi+Ki×Zi)≤Yi)，问这些序列中出现奇数次的数是哪个（只有一个数出现奇数个）？出现了多少次？

思路

注意输入格式，用至少一个空行来分隔每组数据。

有一个数是出现了奇数个，那么设C(x)表示答案是不是<=x（即x过大），具体判断方法是，若<=x的个数有奇数个，那么答案是<=x的，二分搜索即可。

#include <iostream>
#include <cstdio>
#include <sstream>
#include <string>
#include <cstring>
#include <vector>
#include <algorithm>
#include <limits>
using namespace std;
typedef long long ll;
struct ref {
	ll A, B, C;
	ref(ll A, ll B, ll C) : A(A), B(B), C(C) {}
};
vector<ref> refs;
bool C(ll x) { // 判断答案是否<=x，即<=x的个数应该为奇数个。
	ll left = 0;
	for (int i = 0; i < refs.size(); ++i) {
		if (x <= refs[i].B) {
			if (x >= refs[i].A) left += (x - refs[i].A) / refs[i].C + 1;
		}
		else left += (refs[i].B - refs[i].A) / refs[i].C + 1;
	}
	return left & 1;
}
void solve() {
	ll lb = 0, ub = numeric_limits<ll>::max();
	while (ub - lb > 1) {
		ll mid = (ub + lb) >> 1;
		if (C(mid)) ub = mid; // (lb, ub]
		else lb = mid;
	}
	int cnt = 0;
	for (int i = 0; i < refs.size(); ++i)
	if (ub <= refs[i].B && ub >= refs[i].A)
	if ((ub - refs[i].A) % refs[i].C == 0) ++cnt;
	ub == numeric_limits<ll>::max() ? puts("no corruption") : printf("%lld %d\n", ub, cnt);
}
int main() {
	ll A, B, C;
	char line[100];
	while (gets(line)) {
		if (line[0] == 0) {
			if (refs.size()) solve();
			refs.clear();
		}
		else {
			sscanf(line, "%lld%lld%lld", &A, &B, &C);
			refs.push_back(ref(A, B, C));
		}
	}
	if (refs.size()) solve();
	return 0;
}

POJ 3061

题意

给定长度为n的数列a0,a1,⋯,an−1及整数S，求出总和不小于S的连续子序列的长度的最小值。若不存在输出0。

思路

利用前缀和s[k]=num[0]+num[1]+...+num[k]，可知s[i]是单调不减的。然后二分搜索sum[j]≥sum[i]+S即可得最小的j，然后枚举求出最小的j−i。

#include <iostream>
#include <cstdio>
#include <limits>
#include <algorithm>
using namespace std;
int N, S;
int num[100005];
int sum[100005]; // sum[s]=num[0]+num[1]+...+num[s]
void solve() {
	int ans = numeric_limits<int>::max();
	for (int i = 0; i<N; ++i) {
		// printf("i=%d, j=%ld\n", i, lower_bound(sum+i, sum+N, sum[i]+S)-sum);
		// int j = lower_bound(sum+i, sum+N, sum[i]+S) - sum; // 求出最小的j
		int lb = -1, ub = N; // [0, ub)
		while (ub - lb > 1) {
			int mid = (ub + lb) >> 1;
			if (sum[mid] >= sum[i] + S) ub = mid; // (lb, ub]
			else lb = mid;
		}
		// printf("j=%d, ub=%d\n", j , ub);
		if (ub < N && ub > i) ans = min<int>(ans,  ub - i); // 枚举求出最小的j-i
	}
	printf("%d\n", ans == numeric_limits<int>::max() ? 0 : ans);
}
int main() {
	int T;
	scanf("%d", &T);
	while (T--) {
		scanf("%d%d", &N, &S);
		sum[0] = 0;
		for (int i = 0; i < N; ++i) {
			scanf("%d", num + i);
			sum[i] = sum[i - 1 >= 0 ? i - 1 : 0] + num[i];
		}
		solve();
	}
	return 0;
}