MKL库矩阵乘法

此示例是利用Intel 的MKL库函数计算矩阵的乘法，目标为：\(C=\alpha*A*B+\beta*C\)，由函数cblas_dgemm实现；

其中\(A\)为\(m\times k\)维矩阵，\(B\)为\(k\times n\)维矩阵，\(C\)为\(m\times n\)维矩阵。

1 cblas_dgemm参数详解

fun cblas_dgemm(Layout,		//指定行优先(CblasRowMajor,C)或列优先(CblasColMajor,Fortran)数据排序
               TransA,		//指定是否转置矩阵A
               TransB,		//指定是否转置矩阵B
               M,			//矩阵A和C的行数
               N,			//矩阵B和C的列数
               K,			//矩阵A的列，B的行
               alpha,		//矩阵A和B乘积的比例因子
               A,			//A矩阵
               lda,			//矩阵A的第一维的大小
               B,			//B矩阵
               ldb,			//矩阵B的第一维的大小
               beta,		//矩阵C的比例因子
               C,			//(input/output) 矩阵C
               ldc			//矩阵C的第一维的大小
               )

cblas_dgemm矩阵乘法默认的算法就是\(C=\alpha*A*B+\beta*C\)，若只需矩阵\(A\)与\(B\)的乘积，设置\(\alpha=1,\beta=0\)即可。

2 定义待处理矩阵

#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"		// 调用mkl头文件

#define min(x,y) (((x) < (y)) ? (x) : (y))

double* A, * B, * C;		//声明三个矩阵变量，并分配内存
int m, n, k, i, j;			//声明矩阵的维度，其中
double alpha, beta;

m = 2000, k = 200, n = 1000;
alpha = 1.0; beta = 0.0;

A = (double*)mkl_malloc(m * k * sizeof(double), 64);	//按照矩阵维度分配内存
B = (double*)mkl_malloc(k * n * sizeof(double), 64);	//mkl_malloc用法与malloc相似，64表示64位
C = (double*)mkl_malloc(m * n * sizeof(double), 64);
if (A == NULL || B == NULL || C == NULL) {		//判空

    mkl_free(A);
    mkl_free(B);
    mkl_free(C);
    return 1;
}

for (i = 0; i < (m * k); i++) {		//赋值
    A[i] = (double)(i + 1);
}

for (i = 0; i < (k * n); i++) {
    B[i] = (double)(-i - 1);
}

for (i = 0; i < (m * n); i++) {
    C[i] = 0.0;
}

其中\(A\)和\(B\)矩阵设置为：

\[\begin{array}{l}
A = \left[ {\begin{array}{*{20}{c}}
{1.0}&{2.0}& \cdots &{1000.0}\\
{1001.0}&{1002.0}& \cdots &{2000.0}\\
\vdots & \vdots & \ddots & \cdots \\
{999001.0}&{999002.0}& \cdots &{1000000.0}
\end{array}} \right] \space
B = \left[ {\begin{array}{*{20}{c}}
{-1.0}&{-2.0}& \cdots &{-1000.0}\\
{-1001.0}&{-1002.0}& \cdots &{-2000.0}\\
\vdots & \vdots & \ddots & \cdots \\
{-999001.0}&{-999002.0}& \cdots &{-1000000.0}
\end{array}} \right]
\end{array}
\]

\(C\)矩阵为全0。

3 执行矩阵乘法

回到例子中，对照上面的参数，将C矩阵用A与B的矩阵乘法表示：

cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
            m, n, k, alpha, A, k, B, n, beta, C, n);

//在执行完成后，释放内存
mkl_free(A);
mkl_free(B);
mkl_free(C);

执行后的得到结果如下：

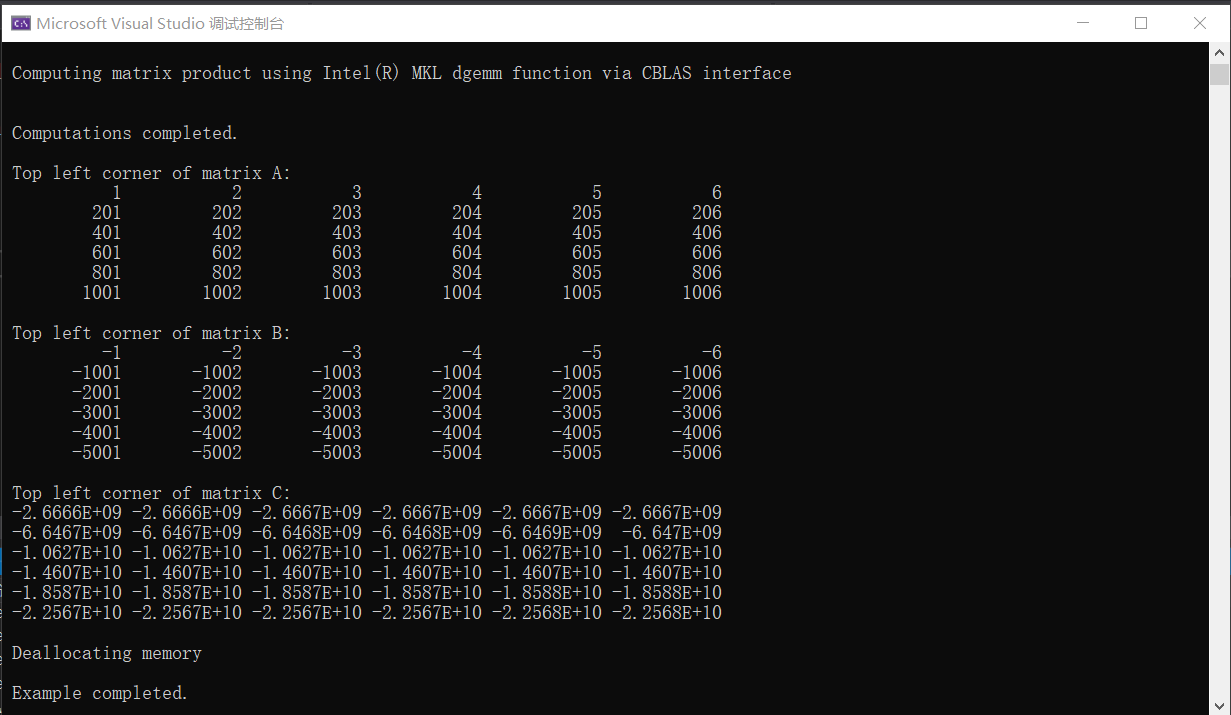
完整代码

#include <stdio.h>
#include <stdlib.h>
#include "mkl.h"

#define min(x,y) (((x) < (y)) ? (x) : (y))

int main()
{
    double* A, * B, * C;
    int m, n, k, i, j;
    double alpha, beta;

    m = 2000, k = 200, n = 1000;

    alpha = 1.0; beta = 0.0;

    A = (double*)mkl_malloc(m * k * sizeof(double), 64);
    B = (double*)mkl_malloc(k * n * sizeof(double), 64);
    C = (double*)mkl_malloc(m * n * sizeof(double), 64);
    if (A == NULL || B == NULL || C == NULL) {

        mkl_free(A);
        mkl_free(B);
        mkl_free(C);
        return 1;
    }

    for (i = 0; i < (m * k); i++) {
        A[i] = (double)(i + 1);
    }

    for (i = 0; i < (k * n); i++) {
        B[i] = (double)(-i - 1);
    }

    for (i = 0; i < (m * n); i++) {
        C[i] = 0.0;
    }

    cblas_dgemm(CblasRowMajor, CblasNoTrans, CblasNoTrans,
        m, n, k, alpha, A, k, B, n, beta, C, n);

    for (i = 0; i < min(m, 6); i++) {
        for (j = 0; j < min(k, 6); j++) {
            printf("%12.0f", A[j + i * k]);
        }
        printf("\n");
    }

    for (i = 0; i < min(k, 6); i++) {
        for (j = 0; j < min(n, 6); j++) {
            printf("%12.0f", B[j + i * n]);
        }
        printf("\n");
    }

    for (i = 0; i < min(m, 6); i++) {
        for (j = 0; j < min(n, 6); j++) {
            printf("%12.5G", C[j + i * n]);
        }
        printf("\n");
    }

    mkl_free(A);
    mkl_free(B);
    mkl_free(C);

    return 0;
}