PCA降维的原理及实现

PCA可以将数据从原来的向量空间映射到新的空间中。由于每次选择的都是方差最大的方向,所以往往经过前几个维度的划分后，之后的数据排列都非常紧密了， 我们可以舍弃这些维度从而实现降维

原理

内积

两个向量的乘积满足:\(ab= |a|\cdot |b|\cdot cos(\theta)\).如果\(|b|=1\)的话,\(ab=|a| \cdot cos(\theta)\). 而这个式子的含义就是a在b方向上的投影长度。pca用投影的长度的方差来衡量一个向量基的好坏。

基变换的矩阵表示

如果我想要把M个N维向量变换到M的R维向量。那么我需要：

• 把每条数据当成行向量X。即m行n列，共m条数据， \(A=(x_1, x_2,...,x_m)^T\)
• 每个基当成一个列向量，按列排成矩阵P， \(P=(p_1, p_2, .., p_k)\)
• XP就是变换的结果

比如有两个基 \((1/\sqrt2, 1/\sqrt2)^T\), \((-1/\sqrt2, 1/\sqrt2)^T\).这是两个正交的基。一个向量\((3, 2)^T\).

\[\begin{pmatrix}
3 & 2
\end{pmatrix}
\begin{bmatrix}
1/\sqrt2 & -1/\sqrt2 \\\\
1/\sqrt2 & 1/\sqrt2 \\\\
\end{bmatrix}
= \begin{pmatrix}
5/\sqrt2 & -1/\sqrt2
\end{pmatrix}
\]

• R个P表示R个基，即新空间有R维，因此 R<=m
• Pi* aj 表示 ai投影到pi上的投影的大小

这里也可以将新空间中的坐标转换回来，先看看他们的关系

\[Y = XP
\]

所以要求X需要计算P的逆矩阵：

\[X = YP^{-1}
\]

由于 \(P \cdot P^T =1\)， 故P是一个可逆矩阵，且模为1，\(P^{-1} = P^T\)。所以最后可以这样计算X：

\[X = YP^{T}
\]

最大化方差理论

每个向量投影到新的空间后，计算所有向量的投影的方差。方差越大，表示数据分布的越"散"。因为数据过于集中就不好处理，数据越散就越容易分开。实际上经过多次投影后，最后几个维度数据往往都集中在一起，这时这些维度就可以舍弃，这就是pca降维的思路。

pca降维的第一步是，让所有向量减去每个特征的平均值。这样会给后面的处理带来非常大的方便。比如计算一个向量的方差：

\[Var(p) = \frac{1}{m} \sum_{i=1}^{m}(p_i-\overline{p})^2
\]

而减去均值后，每个向量的均值都为0，所以可以简化为：

\[Var(p) = \frac{1}{m} \sum_{i=1}^{m}(p_i)^2
\]

注意！！！

这里的均值指的是同一个特征，不同的向量的均值。先通过每一个向量计算出各个特征的均值。再把每个向量的每个特征减去对应的均值。

PCA希望使用相关度最低的基来构建新的向量空间。也就是尽量寻找线性无关的向量（当然最好是正交），这样重合的信息会很少。在pca中，使用协方差来衡量各个特征之间的相关性。

• cov > 0 正相关
• cov == 0 不相关
• cov < 0 负相关

也就是说各个基向量之间满足cov==0就可以了。下面介绍协方差

协方差

协方差的计算公式如下(这里的\(a_i, b_i\)都是数字)：

\[Cov(a, b)=\frac{1}{m} \sum_{i=1}^{n}(a_{i}-\mu_{a})(b_{i}-\mu_{b})=\frac{1}{m} \sum_{i=1}^{m} a_{i} * b_{i}
\]

那么，要使协方差为0，也是ab=0，也就是向量正交！

一般情况下，a，b表示的是两个特征的列向量。并不是一条数据。而是各个数据的两个特征的一个列向量。

协方差矩阵

顾名思义，用矩阵来保存各个特征之前的协方差。如果数据有n个维度（n个特征），那么，他的协方差矩阵\(\sum\)是一个n*n的矩阵。\(\sum_{ij}\) 表示第i和第j个特征的相关度（协方差）.

对于\(m \cdot n\)的数据集X（m条数据集，每条数据n个特征），他的协方差可以通过下面的公式简单的计算出来：

\[\sum = \frac{1}{m} X^T X
\]

也有人写成这种形式， \(x^{(i)}\)表示第i个向量：

\[\frac{1}{m} \sum_{i=1}^{m} x^{(i)} x^{(i)^{T}}
\]

推理如下。（打公式太慢了）

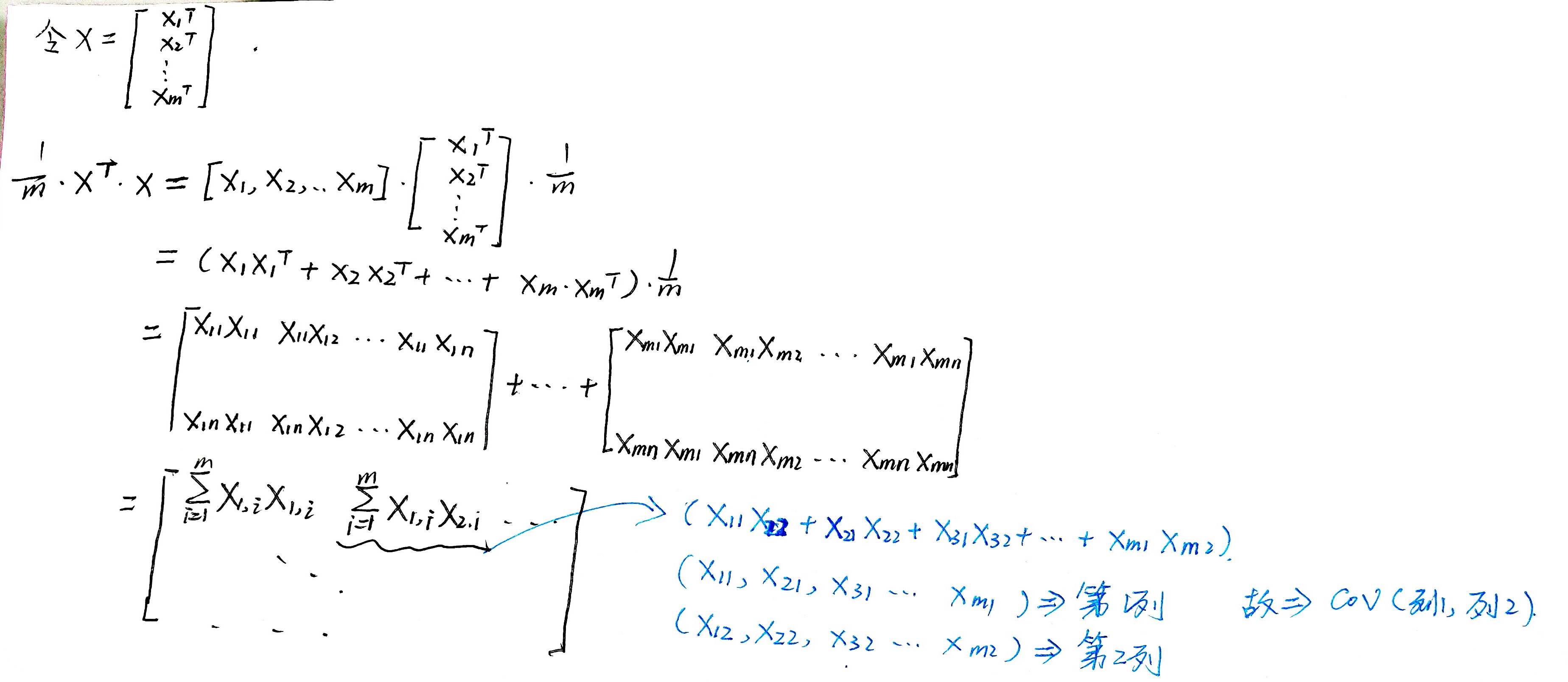
协方差矩阵和PCA

假设有m行n列的数据集 X(这里的X是1.2的X的转置)，X 映射到新的向量空间后的坐标Y, Y的协方差矩阵为D。那么有以下关系：

\[Y = X \cdot P
\]

\[D = \frac{1}{m}Y^T Y = \frac{1}{m}(XP)^T (XP) = P^T\frac{1}{m}(X^TX)P = P^T \sum P
\]

这里的P是\(n*k\)的矩阵，由k的列向量组成，当k小于n时就是降维了。

所以，映射到新的坐标系后的协方差矩阵就是D这里有几点需要注意：

• 1、因为我们希望新的向量基是线性无关的，也就是不同的基之间的协方差应该为0。所以我们要让这个D变成对角矩阵（对角元其实就是方差）
• 2、n维实对称矩阵的性质：一定存在n的线性无关的特征向量。
• 3、通过\(\Lambda = P^TAP\)的方式将实对称矩阵转换维对角矩阵。此时P是用n个线性无关的特征向量（列向量）组成的单位矩阵。\(\Lambda\)是新的向量基对每个维度上的向量对应的方差。
• 4、选择最大的k个 \(\lambda\) 对应的k个特征向量就是我们要求的向量基

实现

linalg.eig(covMat)是numpy的线性代数模块的函数。该函数的api的描述是，返回一个：

归一化（单位“长度”）特征向量，使得列v[:,i]是对应于特征值w[i]

pca的实现真的好简单啊，但是他的原理我花了好久才看明白。心累。

def pca(data, k):
    # DeMean
    dataMean = np.mean(data, axis=0)
    data_demean = data - dataMean

    # 计算协方差矩阵
    covMat = data_demean.T.dot(data_demean) / len(data)

    # 计算cov的特征值和特征向量
    eigVals, eigVects = linalg.eig(covMat)

    # 找到前k大的lambda对应的特征向量
    eigVals_index = np.argsort(-eigVals)    # 前k特征值的索引
    eigVal_wanted = eigVals_index[:k]       # 前k个特征值
    eigVect_wanted = eigVects[:, eigVal_wanted]             # 前k个特征向量
    low_dim_data = data_demean.dot(eigVect_wanted)          # 转换坐标
    recon = low_dim_data.dot(eigVect_wanted.T) + dataMean   # 还原坐标
    return low_dim_data, recon

它可以将高维的数据转换到低维，也可以将转换过的坐标再还原。但是如果是从高维到低维，转换的过程已经损失了一部分数据了，再还原回去时，就和原来不一样了。这样有好也有坏，因为有时候，他还可以去除一些噪音数据。

随机使用一个数据：

X = np.empty((100,2))
X[:, 0] = np.random.uniform(0, 100, 100)
X[:, 1] = 0.75 * X[:, 0] + 3. + np.random.normal(0, 10, 100)

plt.scatter(X[:, 0], X[:, 1])

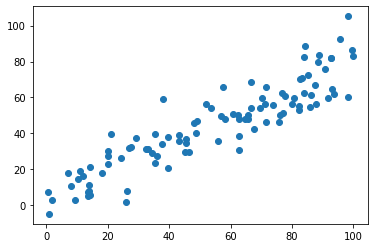
# 2维降1维
low, rec = pca(X, 1)
plt.scatter(rec[:, 0], rec[:,1])

如果，k的维度和原来一样，就可以无损的还原回来。但是如果降低了维度，再还原就会损失数据：

sklearn中的PCA

sklearn中的PCA在 sklearn.decomposition下的PCA中:

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X_train)

X_train_reduction = pca.transform(X_train)
X_test_reduction = pca.transform(X_test)

pca可以直接写浮点数，可以手动少选方差和大于阈值的维度

pca3 = PCA(0.9)
pca3.fit(X_train)

一些参数：

pca2.explained_variance_    # 在各个主成分上的方差
pca2.explained_variance_ratio_    # 各个主成分方差占总方差的比例