git 在 pull 或者合并分支的时候会遇到下图这个界面
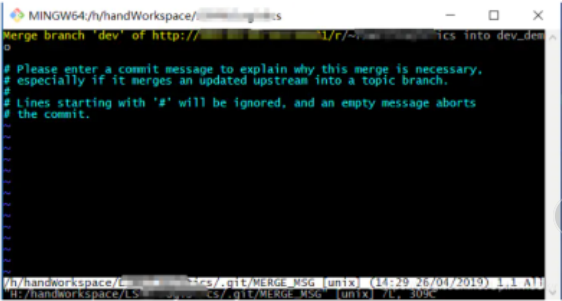
可以不管(直接进入 3, 4 步), 如果要输入解释的话就需要
按键盘字母 i 进入 insert 模式
修改最上面那行黄色合并信息,可以不修改 // 黄色内容为默认的合并信息;
按键盘左上角 "Esc"
输入 " :wq "进行修改后保存退出,然后按回车即可
git 在 pull 或者合并分支的时候会遇到下图这个界面的更多相关文章
- Git:创建与合并分支
1.1创建dev分支,使用命令符 git branch 分支名称. 1.2将HEAD指针切换到dev分支,使用命名符git checkout 分支名称. 注:创建并且转移可以合并为一个步骤,使用命令符 ...
- Git学习——创建与合并分支
分支概念 当前我们所在的分支是master(主分支),可以通过创建分支: git branch <branch_name> 创建完成后,可以查看当前的分支状态: git branch 当前 ...
- git 工作中实用合并分支
合并分支 .克隆远程分支 git clone -b dev1. url .创建本地分支,并关联远程分支 git checkout -b dev_wt orgin/dev_wt .合并某分支到当前分支 ...
- 【Git版本控制】Git的merge合并分支命令
1.实例 git checkout master git merge dev merge合并分支只对当前分支master产生影响,被合并的分支dev不受影响. 假设你有两个分支,“stable” 和 ...
- Git轻松入门2:分支篇
什么是分支 在玩剧情类游戏时,不同的选择会触发不同的剧情路线,每条剧情路线都会独立发展,最终走向不同的结局. Git中所谓的"分支(branch)"就如同游戏中的剧情路线,用户可以 ...
- git的工作流程(分支合并)
git支持很多种工作流程,我们采用的一般是这样,远程创建一个主分支,本地每人创建功能分支,日常工作流程如下: 去自己的工作分支$ git checkout work 工作.... 提交工作分支的修改$ ...
- git总结三、关于分支下——团队合作中最重要的合并分支
合并分支是团队合作开发中常见的操作,这里涉及到两个命令:git merge 和 git rebase 下面来好好说一下git merge和git rebase都是怎样工作的 一. 1.新建一个空目录并 ...
- git命令合并分支代码
对于复杂的系统,我们可能要开好几个分支来开发,那么怎样使用git合并分支呢? 合并步骤:1.进入要合并的分支(如开发分支合并到master,则进入master目录)git checkout maste ...
- git 合并分支到master
git 合并分支到master 假如我们现在在dev分支上,刚开发完项目,执行了下列命令 git add .git commit -m ‘dev'git push -u origin dev 然后 ...
随机推荐
- 内网穿透工具--NPS
一.简介 NPS是一款轻量级,高性能,强大功能的内网穿透代理服务器.目前支持TCP,UDP流量转发,可支持任何TCP,UDP上层协议(访问内网网站,本地支付接口调试,SSH访问,远程桌面,内网dns解 ...
- 一个最简单的Dubbo入门框架
Dubbo背景和简介 Dubbo开始于电商系统,因此在这里先从电商系统的演变讲起. 1.单一应用框架(ORM) 当网站流量很小时,只需一个应用,将所有功能如下单支付等都部署在一起,以减少部署节点和成本 ...
- React优点?
声明式, 组件化, 一次学习, 随处编写. 灵活, 丰富, 轻巧, 高效
- xml文件使用DOM解析,报异常org.xml.sax.SAXParseException,"characterEncoding" 的引用必须以 ';' 分隔符结尾异常
这个异常一般为xml文件对&的报错,只需要将&改为转义后的&即可解决
- Linux 网卡配置参数
网卡配置文件位于 /etc/sysconfig/network-scripts/ 目录下 网卡配置文件在RHEL5/6以eth为网卡文件的前缀,在RHEL7中以ifcfg为网卡文件的前缀 配置 解释 ...
- nginx使用与配置
一.nginx操作命令 nginx常用命令: 验证配置是否正确: nginx -t 查看Nginx的版本号:nginx -V 启动Nginx:start nginx 重新加载nginx:nginx.e ...
- java-jsp-learnning
简介:JSP(全称Java Server Pages) 一种动态网页开发技术.它使用JSP标签在HTML网页中插入Java代码.标签通常以<%开头以%>结束. JSP是一种Java ser ...
- Dubbo 推荐用什么协议?
dubbo://(推荐) rmi:// hessian:// http:// webservice:// thrift:// memcached:// redis:// rest://
- ROS学习文章
ros机器人到底有没有必要学习?
- jq easyui数据网络的分页过程
第一次写技术方面的文章,有点忐忑,总怕自己讲的不对误导别人.但是万事总有个开头,有不足错误之处,请各位读者老爷指出. 言归正传,最近刚进新公司,上头要求我先熟悉熟悉easyui这个组件库.在涉及到da ...
