2022-05-22：给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。 百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p

2022-05-22：给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。

如何时间复杂度O(N)，额外空间复杂度O(1)，解决最低公共祖先问题?

力扣236。二叉树的最近公共祖先。

答案2022-05-23：

莫里斯遍历。主要是修改rust代码。

rust代码修改如下：

use std::cell::RefCell;
use std::rc::Rc;

fn main() {
    let mut head = Some(Rc::new(RefCell::new(TreeNode::new(1))));
    let mut left_left = Some(Rc::new(RefCell::new(TreeNode::new(4))));
    let mut left_right = Some(Rc::new(RefCell::new(TreeNode::new(5))));
    head.as_ref().unwrap().borrow_mut().left = Some(Rc::new(RefCell::new(TreeNode::new(2))));
    head.as_ref().unwrap().borrow_mut().right = Some(Rc::new(RefCell::new(TreeNode::new(3))));
    head.as_ref()
        .unwrap()
        .borrow()
        .left
        .as_ref()
        .unwrap()
        .borrow_mut()
        .left = Some(Rc::clone(&left_left.as_ref().unwrap()));
    head.as_ref()
        .unwrap()
        .borrow()
        .left
        .as_ref()
        .unwrap()
        .borrow_mut()
        .right = Some(Rc::clone(&left_right.as_ref().unwrap()));
    let ans = Solution::lowest_common_ancestor(
        Some(Rc::clone(&head.as_ref().unwrap())),
        Some(Rc::clone(&left_left.as_ref().unwrap())),
        Some(Rc::clone(&left_right.as_ref().unwrap())),
    );
    if ans.is_none() {
        println!("ans = 空");
    } else {
        println!("ans val = {}", ans.as_ref().unwrap().borrow().val);
    }
    println!("-----------------");
    println!("head = {}", head.as_ref().unwrap().borrow().val);
    println!(
        "head.left = {}",
        head.as_ref()
            .unwrap()
            .borrow()
            .left
            .as_ref()
            .unwrap()
            .borrow()
            .val
    );
    println!(
        "head.right = {}",
        head.as_ref()
            .unwrap()
            .borrow()
            .right
            .as_ref()
            .unwrap()
            .borrow()
            .val
    );
    println!(
        "head.left.left = {}",
        head.as_ref()
            .unwrap()
            .borrow()
            .left
            .as_ref()
            .unwrap()
            .borrow()
            .left
            .as_ref()
            .unwrap()
            .borrow()
            .val
    );
    println!(
        "head.left.right = {}",
        head.as_ref()
            .unwrap()
            .borrow()
            .left
            .as_ref()
            .unwrap()
            .borrow()
            .right
            .as_ref()
            .unwrap()
            .borrow()
            .val
    );
}

pub struct TreeNode {
    pub val: i32,
    pub left: Option<Rc<RefCell<TreeNode>>>,
    pub right: Option<Rc<RefCell<TreeNode>>>,
}

impl TreeNode {
    pub fn new(val: i32) -> Self {
        Self {
            val,
            left: None,
            right: None,
        }
    }
}

pub struct Solution {}

// 力扣里提交以下的代码
impl Solution {
    // 该方法亮点在于：时间复杂度O(N)，额外空间复杂度O(1)
    pub fn lowest_common_ancestor(
        mut head: Option<Rc<RefCell<TreeNode>>>,
        mut o1: Option<Rc<RefCell<TreeNode>>>,
        mut o2: Option<Rc<RefCell<TreeNode>>>,
    ) -> Option<Rc<RefCell<TreeNode>>> {
        // if (findFirst(o1.left, o1, o2) != null || findFirst(o1.right, o1, o2) != null) {
        //     return o1;
        // }
        if !find_first(
            if o1.as_ref().unwrap().borrow().left.is_none() {
                None
            } else {
                Some(Rc::clone(
                    &o1.as_ref().unwrap().borrow().left.as_ref().unwrap(),
                ))
            },
            if o1.is_none() {
                None
            } else {
                Some(Rc::clone(&o1.as_ref().unwrap()))
            },
            if o2.is_none() {
                None
            } else {
                Some(Rc::clone(&o2.as_ref().unwrap()))
            },
        )
        .is_none()
            || !find_first(
                if o1.as_ref().unwrap().borrow().right.is_none() {
                    None
                } else {
                    Some(Rc::clone(
                        &o1.as_ref().unwrap().borrow().right.as_ref().unwrap(),
                    ))
                },
                if o1.is_none() {
                    None
                } else {
                    Some(Rc::clone(&o1.as_ref().unwrap()))
                },
                if o2.is_none() {
                    None
                } else {
                    Some(Rc::clone(&o2.as_ref().unwrap()))
                },
            )
            .is_none()
        {
            return if o1.is_none() {
                None
            } else {
                Some(Rc::clone(&o1.as_ref().unwrap()))
            };
        }

        // if (findFirst(o2.left, o1, o2) != null || findFirst(o2.right, o1, o2) != null) {
        // 	return o2;
        // }
        if !find_first(
            if o2.as_ref().unwrap().borrow().left.is_none() {
                None
            } else {
                Some(Rc::clone(
                    &o2.as_ref().unwrap().borrow().left.as_ref().unwrap(),
                ))
            },
            if o1.is_none() {
                None
            } else {
                Some(Rc::clone(&o1.as_ref().unwrap()))
            },
            if o2.is_none() {
                None
            } else {
                Some(Rc::clone(&o2.as_ref().unwrap()))
            },
        )
        .is_none()
            || !find_first(
                if o2.as_ref().unwrap().borrow().right.is_none() {
                    None
                } else {
                    Some(Rc::clone(
                        &o2.as_ref().unwrap().borrow().right.as_ref().unwrap(),
                    ))
                },
                if o1.is_none() {
                    None
                } else {
                    Some(Rc::clone(&o1.as_ref().unwrap()))
                },
                if o2.is_none() {
                    None
                } else {
                    Some(Rc::clone(&o2.as_ref().unwrap()))
                },
            )
            .is_none()
        {
            return if o2.is_none() {
                None
            } else {
                Some(Rc::clone(&o2.as_ref().unwrap()))
            };
        }

        //left_aim := findFirst(head, o1, o2)
        let mut left_aim = find_first(
            if head.is_none() {
                None
            } else {
                Some(Rc::clone(&head.as_ref().unwrap()))
            },
            if o1.is_none() {
                None
            } else {
                Some(Rc::clone(&o1.as_ref().unwrap()))
            },
            if o2.is_none() {
                None
            } else {
                Some(Rc::clone(&o2.as_ref().unwrap()))
            },
        );
        // TreeNode cur = head;
        let mut cur = if head.is_none() {
            None
        } else {
            Some(Rc::clone(&head.as_ref().unwrap()))
        };
        // TreeNode most_right = null;
        let mut most_right: Option<Rc<RefCell<TreeNode>>> = None;
        // TreeNode ans = null;
        let mut ans: Option<Rc<RefCell<TreeNode>>> = None;
        //for cur != nil {
        while !cur.is_none() {
            // 	most_right = cur.left;
            most_right = if cur.as_ref().unwrap().borrow().left.is_none() {
                None
            } else {
                Some(Rc::clone(
                    &cur.as_ref().unwrap().borrow().left.as_ref().unwrap(),
                ))
            };

            //if most_right != nil {
            if !most_right.is_none() {
                //while most_right.right != null && most_right.right != cur {
                while !most_right.as_ref().unwrap().borrow().right.is_none()
                    && !is_eq(
                        &Some(Rc::clone(
                            &most_right
                                .as_ref()
                                .unwrap()
                                .borrow()
                                .right
                                .as_ref()
                                .unwrap(),
                        )),
                        &cur,
                    )
                {
                    // 			most_right = most_right.right;
                    most_right = if most_right.as_ref().unwrap().borrow().right.is_none() {
                        None
                    } else {
                        Some(Rc::clone(
                            &most_right
                                .as_ref()
                                .unwrap()
                                .borrow()
                                .right
                                .as_ref()
                                .unwrap(),
                        ))
                    };
                }

                //if (most_right.right == null) {
                if most_right.as_ref().unwrap().borrow().right.is_none() {
                    // 			most_right.right = cur;
                    most_right.as_ref().unwrap().borrow_mut().right = if cur.is_none() {
                        None
                    } else {
                        Some(Rc::clone(&cur.as_ref().unwrap()))
                    };
                    // 			cur = cur.left;
                    cur = if cur.as_ref().unwrap().borrow().left.is_none() {
                        None
                    } else {
                        Some(Rc::clone(
                            &cur.as_ref().unwrap().borrow().left.as_ref().unwrap(),
                        ))
                    };
                    continue;
                } else {
                    //most_right.right = null;
                    most_right.as_ref().unwrap().borrow_mut().right = None;
                    //if (findLeftAim(cur.left, left_aim)) {
                    if find_left_aim(
                        if cur.as_ref().unwrap().borrow().left.is_none() {
                            None
                        } else {
                            Some(Rc::clone(
                                &cur.as_ref().unwrap().borrow().left.as_ref().unwrap(),
                            ))
                        },
                        if left_aim.is_none() {
                            None
                        } else {
                            Some(Rc::clone(&left_aim.as_ref().unwrap()))
                        },
                    ) {
                        //if (ans == null && findFirst(left_aim.right, o1, o2) != null) {
                        if ans.is_none()
                            && !find_first(
                                if left_aim.as_ref().unwrap().borrow().right.is_none() {
                                    None
                                } else {
                                    Some(Rc::clone(
                                        &left_aim
                                            .as_ref()
                                            .unwrap()
                                            .borrow()
                                            .right
                                            .as_ref()
                                            .unwrap(),
                                    ))
                                },
                                if o1.is_none() {
                                    None
                                } else {
                                    Some(Rc::clone(&o1.as_ref().unwrap()))
                                },
                                if o2.is_none() {
                                    None
                                } else {
                                    Some(Rc::clone(&o2.as_ref().unwrap()))
                                },
                            )
                            .is_none()
                        {
                            //ans = left_aim;
                            ans = if left_aim.is_none() {
                                None
                            } else {
                                Some(Rc::clone(&left_aim.as_ref().unwrap()))
                            };
                        }

                        // left_aim = cur;
                        left_aim = if cur.is_none() {
                            None
                        } else {
                            Some(Rc::clone(&cur.as_ref().unwrap()))
                        };
                    }
                }
            }
            // 	cur = cur.right;
            cur = if cur.as_ref().unwrap().borrow().right.is_none() {
                None
            } else {
                Some(Rc::clone(
                    &cur.as_ref().unwrap().borrow().right.as_ref().unwrap(),
                ))
            };
        }

        if !ans.is_none() {
            return ans;
        } else {
            if !find_first(
                if left_aim.as_ref().unwrap().borrow().right.is_none() {
                    None
                } else {
                    Some(Rc::clone(
                        &left_aim.as_ref().unwrap().borrow().right.as_ref().unwrap(),
                    ))
                },
                if o1.is_none() {
                    None
                } else {
                    Some(Rc::clone(&o1.as_ref().unwrap()))
                },
                if o2.is_none() {
                    None
                } else {
                    Some(Rc::clone(&o2.as_ref().unwrap()))
                },
            )
            .is_none()
            {
                return Some(Rc::clone(&left_aim.as_ref().unwrap()));
            } else {
                return Some(Rc::clone(&head.as_ref().unwrap()));
            }
        }
    }
}

fn find_left_aim(
    mut head: Option<Rc<RefCell<TreeNode>>>,
    mut left_aim: Option<Rc<RefCell<TreeNode>>>,
) -> bool {
    let mut tail = reverse_edge(Some(Rc::clone(&head.as_ref().unwrap())));
    //TreeNode cur = tail;
    let mut cur = if tail.is_none() {
        None
    } else {
        Some(Rc::clone(&tail.as_ref().unwrap()))
    };
    // boolean ans = false;
    let mut ans = false;
    while !cur.is_none() {
        if is_eq(&cur, &left_aim) {
            ans = true;
        }
        // 	cur = cur.right;
        cur = if cur.as_ref().unwrap().borrow().right.is_none() {
            None
        } else {
            Some(Rc::clone(
                &cur.as_ref().unwrap().borrow().right.as_ref().unwrap(),
            ))
        };
    }
    reverse_edge(Some(Rc::clone(&tail.as_ref().unwrap())));
    return ans;
}

fn reverse_edge(mut from: Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
    //TreeNode pre = null;
    let mut pre: Option<Rc<RefCell<TreeNode>>> = None;
    //TreeNode next = null;
    let mut next: Option<Rc<RefCell<TreeNode>>> = None;
    while !is_eq(&from, &None) {
        // next = from.right;
        next = if from.as_ref().unwrap().borrow().right.is_none() {
            None
        } else {
            Some(Rc::clone(
                &from.as_ref().unwrap().borrow().right.as_ref().unwrap(),
            ))
        };
        // from.right = pre;
        from.as_ref().unwrap().borrow_mut().right = if pre.is_none() {
            None
        } else {
            Some(Rc::clone(&pre.as_ref().unwrap()))
        };
        // pre = from;
        pre = if from.is_none() {
            None
        } else {
            Some(Rc::clone(&from.as_ref().unwrap()))
        };
        // from = next;
        from = if next.is_none() {
            None
        } else {
            Some(Rc::clone(&next.as_ref().unwrap()))
        };
    }
    return pre;
}

fn find_first(
    mut head: Option<Rc<RefCell<TreeNode>>>,
    mut o1: Option<Rc<RefCell<TreeNode>>>,
    mut o2: Option<Rc<RefCell<TreeNode>>>,
) -> Option<Rc<RefCell<TreeNode>>> {
    //if head == nil {
    if head.is_none() {
        return None;
    }
    //cur := head
    let mut cur: Option<Rc<RefCell<TreeNode>>> = Some(Rc::clone(&head.as_ref().unwrap()));
    //var most_right *TreeNode
    let mut most_right: Option<Rc<RefCell<TreeNode>>> = None;
    //var first *TreeNode
    let mut first: Option<Rc<RefCell<TreeNode>>> = None;
    //for cur != nil {
    while !cur.is_none() {
        //most_right = cur.left;
        most_right = if cur.as_ref().unwrap().borrow().left.is_none() {
            None
        } else {
            Some(Rc::clone(
                &cur.as_ref().unwrap().borrow().left.as_ref().unwrap(),
            ))
        };

        //if most_right != nil {
        if !most_right.is_none() {
            while !most_right.as_ref().unwrap().borrow().right.is_none()
                && !is_eq(&most_right.as_ref().unwrap().borrow().right, &cur)
            {
                //most_right = most_right.right;
                most_right = if most_right.as_ref().unwrap().borrow().right.is_none() {
                    None
                } else {
                    Some(Rc::clone(
                        &most_right
                            .as_ref()
                            .unwrap()
                            .borrow()
                            .right
                            .as_ref()
                            .unwrap(),
                    ))
                };
            }
            if is_eq(&most_right.as_ref().unwrap().borrow().right, &None) {
                if is_eq(&first, &None) && (is_eq(&cur, &o1) || is_eq(&cur, &o2)) {
                    //             first = cur;
                    first = if cur.is_none() {
                        None
                    } else {
                        Some(Rc::clone(&cur.as_ref().unwrap()))
                    };
                }
                //         most_right.right = cur;
                most_right.as_ref().unwrap().borrow_mut().right = if cur.is_none() {
                    None
                } else {
                    Some(Rc::clone(&cur.as_ref().unwrap()))
                };
                //         cur = cur.left;
                cur = if cur.as_ref().unwrap().borrow().left.is_none() {
                    None
                } else {
                    Some(Rc::clone(
                        &cur.as_ref().unwrap().borrow().left.as_ref().unwrap(),
                    ))
                };
                continue;
            } else {
                //most_right.right = nil;
                most_right.as_ref().unwrap().borrow_mut().right = None;
            }
        } else {
            //if first == nil && (cur == o1 || cur == o2) {
            if is_eq(&first, &None) && (is_eq(&cur, &o1) || is_eq(&cur, &o2)) {
                //         first = cur;
                first = if cur.as_ref().is_none() {
                    None
                } else {
                    Some(Rc::clone(&cur.as_ref().unwrap()))
                };
            }
        }
        // cur = cur.right;
        cur = if cur.as_ref().unwrap().borrow().right.is_none() {
            None
        } else {
            Some(Rc::clone(
                &cur.as_ref().unwrap().borrow().right.as_ref().unwrap(),
            ))
        };
    }
    return first;
}

fn is_eq(o1: &Option<Rc<RefCell<TreeNode>>>, o2: &Option<Rc<RefCell<TreeNode>>>) -> bool {
    if o1.is_none() && o2.is_none() {
        return true;
    }
    if o1.is_none() || o2.is_none() {
        return false;
    }
    return o1.as_ref().unwrap().borrow().val == o2.as_ref().unwrap().borrow().val;
}

执行结果如下：

---

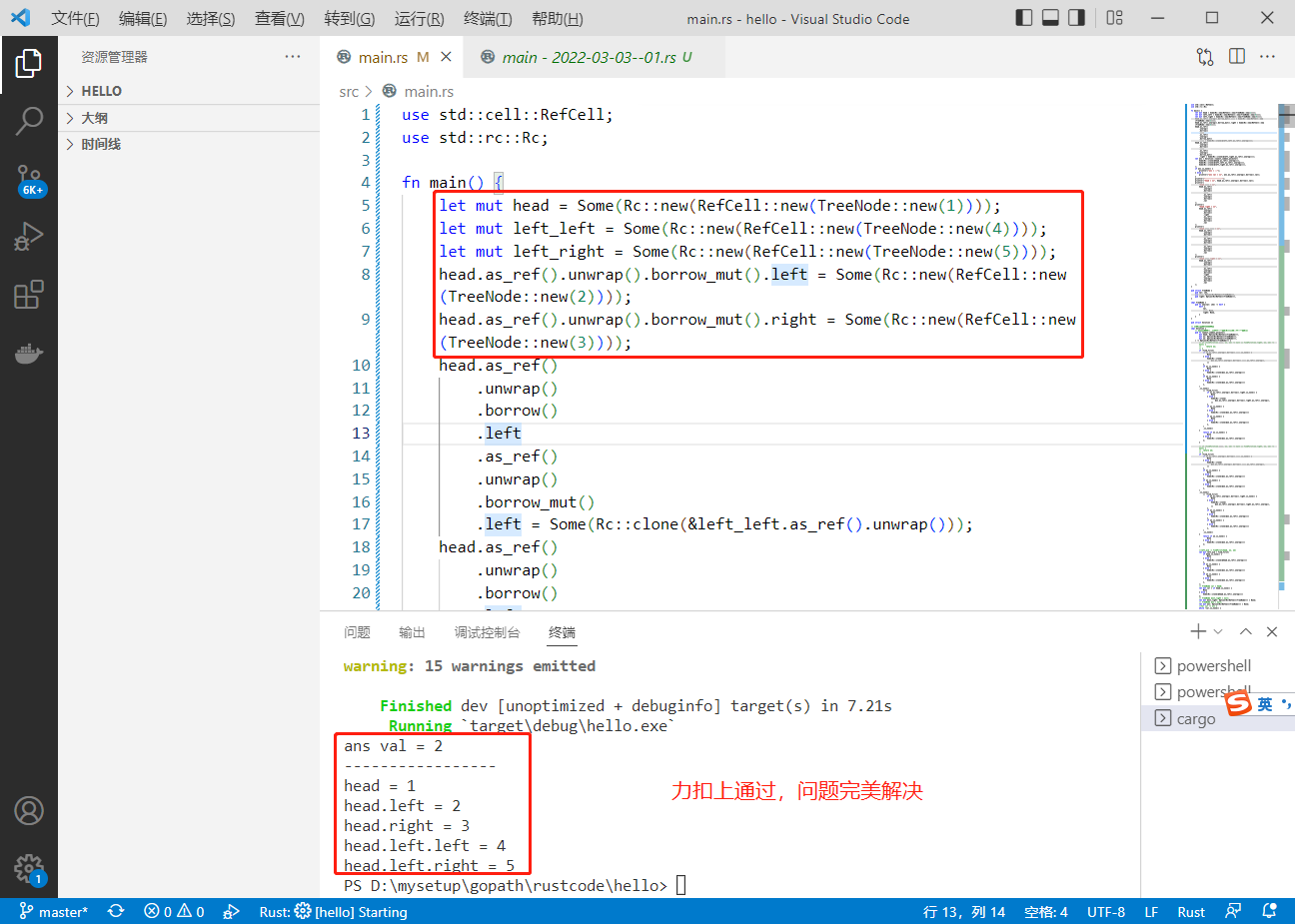
答案2022-05-22：

莫里斯遍历。

答案用rust编写，答案有误。代码如下：

use std::cell::RefCell;
use std::rc::Rc;

fn main() {
    let mut head = Rc::new(RefCell::new(Some(TreeNode::new(3))));
    let mut left = Rc::clone(&head.borrow().as_ref().unwrap().left);
    *left.borrow_mut() = Some(TreeNode::new(5));

    let mut right = Rc::clone(&head.borrow().as_ref().unwrap().right);
    *right.borrow_mut() = Some(TreeNode::new(1));

    let mut head2 = Rc::clone(&head.borrow().as_ref().unwrap().left);
    let mut leftleft = Rc::clone(&head2.borrow().as_ref().unwrap().left);
    *leftleft.borrow_mut() = Some(TreeNode::new(6));

    let mut rightright = Rc::clone(&head2.borrow().as_ref().unwrap().right);
    *rightright.borrow_mut() = Some(TreeNode::new(2));

    let ans = lowest_common_ancestor(
        Rc::clone(&head),
        Rc::clone(&leftleft),
        Rc::clone(&rightright),
    );
    if ans.borrow().is_none() {
        println!("None");
    } else {
        println!("ans = {}", ans.borrow().as_ref().unwrap().val);
    }

    let mut left = Rc::clone(&head.borrow().as_ref().unwrap().left);
    let mut right = Rc::clone(&head.borrow().as_ref().unwrap().right);
    println!("head = {}", head.borrow().as_ref().unwrap().val);
    println!("p = {}", left.borrow().as_ref().unwrap().val);
    println!("q = {}", right.borrow().as_ref().unwrap().val);

    println!("---------------");
    println!("head = {}", head.borrow().as_ref().unwrap().val);
    println!("left = {}", left.borrow().as_ref().unwrap().val);
    println!("right = {}", right.borrow().as_ref().unwrap().val);
    println!("left.left = {}", leftleft.borrow().as_ref().unwrap().val);
    println!("left.right = {}", rightright.borrow().as_ref().unwrap().val);
}

pub struct TreeNode {
    pub val: i32,
    pub left: Rc<RefCell<Option<TreeNode>>>,
    pub right: Rc<RefCell<Option<TreeNode>>>,
}

impl TreeNode {
    pub fn new(val: i32) -> Self {
        Self {
            val,
            left: Rc::new(RefCell::new(None)),
            right: Rc::new(RefCell::new(None)),
        }
    }
}

fn lowest_common_ancestor(
    mut head: Rc<RefCell<Option<TreeNode>>>,
    mut o1: Rc<RefCell<Option<TreeNode>>>,
    mut o2: Rc<RefCell<Option<TreeNode>>>,
) -> Rc<RefCell<Option<TreeNode>>> {
    if !find_first(
        Rc::clone(&o1.borrow().as_ref().unwrap().left),
        Rc::clone(&o1),
        Rc::clone(&o2),
    )
    .borrow()
    .is_none()
        || !find_first(
            Rc::clone(&o1.borrow().as_ref().unwrap().right),
            Rc::clone(&o1),
            Rc::clone(&o2),
        )
        .borrow()
        .is_none()
    {
        return Rc::clone(&o1);
    }

    if !find_first(
        Rc::clone(&o2.borrow().as_ref().unwrap().left),
        Rc::clone(&o1),
        Rc::clone(&o2),
    )
    .borrow()
    .is_none()
        || !find_first(
            Rc::clone(&o2.borrow().as_ref().unwrap().right),
            Rc::clone(&o1),
            Rc::clone(&o2),
        )
        .borrow()
        .is_none()
    {
        return Rc::clone(&o1);
    }
    let mut left_aim: Rc<RefCell<Option<TreeNode>>> =
        find_first(Rc::clone(&head), Rc::clone(&o1), Rc::clone(&o2));
    let mut cur: Rc<RefCell<Option<TreeNode>>> = Rc::clone(&head);
    let mut most_right: Rc<RefCell<Option<TreeNode>>> = Rc::new(RefCell::new(None));
    let mut ans: Rc<RefCell<Option<TreeNode>>> = Rc::new(RefCell::new(None));
    while cur.borrow().is_none() {
        most_right = Rc::clone(&cur.borrow().as_ref().unwrap().left);
        if !most_right.borrow().is_none() {
            while !Rc::clone(&most_right.borrow().as_ref().unwrap().right)
                .borrow()
                .is_none()
                && is_eq(
                    Rc::clone(&most_right.borrow().as_ref().unwrap().right),
                    Rc::clone(&cur),
                )
            {
                let mut mostrightright = Rc::clone(&most_right.borrow().as_ref().unwrap().right);
                most_right = Rc::clone(&mostrightright);
            }
            if Rc::clone(&most_right.borrow().as_ref().unwrap().right)
                .borrow()
                .is_none()
            {
                let mut mostrightright = Rc::clone(&most_right.borrow().as_ref().unwrap().right);
                mostrightright = Rc::clone(&cur);
                let mut curleft = Rc::clone(&cur.borrow().as_ref().unwrap().left);
                cur = Rc::clone(&curleft);
                continue;
            } else {
                let mut mostrightright = Rc::clone(&most_right.borrow().as_ref().unwrap().right);
                mostrightright = Rc::new(RefCell::new(None));
                if find_left_aim(
                    Rc::clone(&cur.borrow().as_ref().unwrap().left),
                    Rc::clone(&left_aim),
                ) {
                    if ans.borrow().is_none()
                        && !find_first(
                            Rc::clone(&left_aim.borrow().as_ref().unwrap().right),
                            Rc::clone(&o1),
                            Rc::clone(&o2),
                        )
                        .borrow()
                        .is_none()
                    {
                        ans = Rc::clone(&left_aim);
                    }
                    left_aim = Rc::clone(&cur);
                }
            }
        }
        let mut curright = Rc::clone(&cur.borrow().as_ref().unwrap().right);
        cur = Rc::clone(&curright);
    }
    return if !ans.borrow().is_none() {
        ans
    } else {
        if !find_first(
            Rc::clone(&left_aim.borrow().as_ref().unwrap().right),
            Rc::clone(&o1),
            Rc::clone(&o2),
        )
        .borrow()
        .is_none()
        {
            Rc::clone(&left_aim)
        } else {
            Rc::clone(&head)
        }
    };
}
fn is_eq(mut a: Rc<RefCell<Option<TreeNode>>>, mut b: Rc<RefCell<Option<TreeNode>>>) -> bool {
    if a.borrow().is_none() && b.borrow().is_none() {
        return true;
    }
    if a.borrow().is_none() || b.borrow().is_none() {
        return false;
    }
    return a.borrow().as_ref().unwrap().val == b.borrow().as_ref().unwrap().val;
}

fn find_left_aim(
    mut head: Rc<RefCell<Option<TreeNode>>>,
    mut left_aim: Rc<RefCell<Option<TreeNode>>>,
) -> bool {
    let mut tail = reverse_edge(head);
    let mut cur = Rc::clone(&tail);
    let mut ans = false;
    while !cur.borrow().is_none() {
        if is_eq(Rc::clone(&cur), Rc::clone(&left_aim)) {
            ans = true;
        }
        let mut curright = Rc::clone(&cur.borrow().as_ref().unwrap().right);
        cur = Rc::clone(&curright);
    }
    reverse_edge(tail);
    return ans;
}

fn reverse_edge(mut from: Rc<RefCell<Option<TreeNode>>>) -> Rc<RefCell<Option<TreeNode>>> {
    let mut pre: Rc<RefCell<Option<TreeNode>>> = Rc::new(RefCell::new(None));
    let mut next: Rc<RefCell<Option<TreeNode>>> = Rc::new(RefCell::new(None));
    while !from.borrow().is_none() {
        next = Rc::clone(&from.borrow().as_ref().unwrap().right);
        {
            let mut fromright = Rc::clone(&from.borrow().as_ref().unwrap().right);
            fromright = Rc::clone(&pre); //此处错误
        }
        pre = Rc::clone(&from);
        from = Rc::clone(&next);
    }
    return pre;
}

fn find_first(
    mut head: Rc<RefCell<Option<TreeNode>>>,
    mut o1: Rc<RefCell<Option<TreeNode>>>,
    mut o2: Rc<RefCell<Option<TreeNode>>>,
) -> Rc<RefCell<Option<TreeNode>>> {
    if head.borrow().is_none() {
        return Rc::new(RefCell::new(None));
    }
    let mut cur: Rc<RefCell<Option<TreeNode>>> = Rc::clone(&head);
    let mut most_right: Rc<RefCell<Option<TreeNode>>> = Rc::new(RefCell::new(None));
    let mut first: Rc<RefCell<Option<TreeNode>>> = Rc::new(RefCell::new(None));
    while !cur.borrow().is_none() {
        most_right = Rc::clone(&cur.borrow().as_ref().unwrap().left);
        if !most_right.borrow().is_none() {
            while !Rc::clone(&most_right.borrow().as_ref().unwrap().right)
                .borrow()
                .is_none()
                && !is_eq(
                    Rc::clone(&most_right.borrow().as_ref().unwrap().right),
                    Rc::clone(&cur),
                )
            {
                let mut most_right_right = Rc::clone(&most_right.borrow().as_ref().unwrap().right);
                most_right = Rc::clone(&most_right_right);
            }
            if Rc::clone(&most_right.borrow().as_ref().unwrap().right)
                .borrow()
                .is_none()
            {
                if !first.borrow().is_none()
                    && (is_eq(Rc::clone(&cur), Rc::clone(&o1))
                        || is_eq(Rc::clone(&cur), Rc::clone(&o2)))
                {
                    first = Rc::clone(&cur);
                }

                let mut most_right_right = Rc::clone(&most_right.borrow().as_ref().unwrap().right);
                most_right_right = Rc::clone(&cur); //此处错误
                let mut curleft = Rc::clone(&cur.borrow().as_ref().unwrap().left);
                cur = Rc::clone(&curleft);
                continue;
            } else {
                let mut most_right_right = Rc::clone(&most_right.borrow().as_ref().unwrap().right);
                most_right_right = Rc::new(RefCell::new(None)); //此处错误
            }
        } else {
            if first.borrow().is_none()
                && (is_eq(Rc::clone(&cur), Rc::clone(&o1))
                    || is_eq(Rc::clone(&cur), Rc::clone(&o2)))
            {
                first = Rc::clone(&cur);
            }
            first = Rc::clone(&cur);
        }
        let mut curright = Rc::clone(&cur.borrow().as_ref().unwrap().right);
        cur = Rc::clone(&curright);
    }
    return first;
}

执行结果如下：

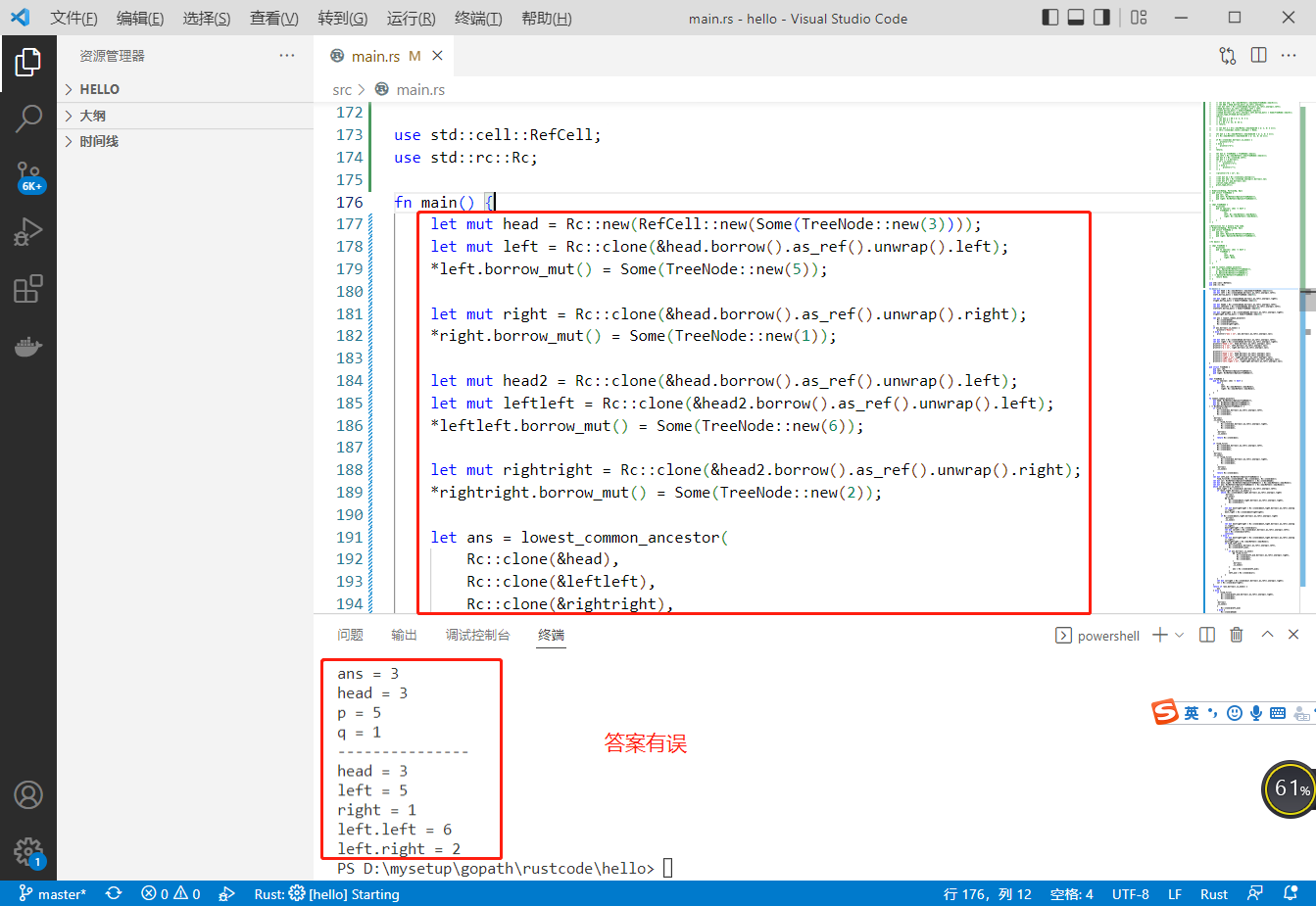
答案用golang编写。代码如下：

package main

import "fmt"

func main() {
	head := &TreeNode{val: 3}
	head.left = &TreeNode{val: 5}
	head.right = &TreeNode{val: 1}
	head.left.left = &TreeNode{val: 6}
	head.left.right = &TreeNode{val: 2}
	ans := lowestCommonAncestor(head, head.left.left, head.left.right)
	fmt.Println(ans.val)
}

// Definition for a binary tree node.
type TreeNode struct {
	val   int
	left  *TreeNode
	right *TreeNode
}

// 提交以下的方法
// 该方法亮点在于：时间复杂度O(N)，额外空间复杂度O(1)
func lowestCommonAncestor(head, o1, o2 *TreeNode) *TreeNode {
	if findFirst(o1.left, o1, o2) != nil || findFirst(o1.right, o1, o2) != nil {
		return o1
	}
	if findFirst(o2.left, o1, o2) != nil || findFirst(o2.right, o1, o2) != nil {
		return o2
	}
	leftAim := findFirst(head, o1, o2)
	cur := head
	var mostRight *TreeNode
	var ans *TreeNode
	for cur != nil {
		mostRight = cur.left
		if mostRight != nil {
			for mostRight.right != nil && mostRight.right != cur {
				mostRight = mostRight.right
			}
			if mostRight.right == nil {
				mostRight.right = cur
				cur = cur.left
				continue
			} else {
				mostRight.right = nil
				if findLeftAim(cur.left, leftAim) {
					if ans == nil && findFirst(leftAim.right, o1, o2) != nil {
						ans = leftAim
					}
					leftAim = cur
				}
			}
		}
		cur = cur.right
	}
	if ans != nil {
		return ans
	} else {
		if findFirst(leftAim.right, o1, o2) != nil {
			return leftAim
		} else {
			return head
		}
	}
}

func findLeftAim(head, leftAim *TreeNode) bool {
	tail := reverseEdge(head)
	cur := tail
	ans := false
	for cur != nil {
		if cur == leftAim {
			ans = true
		}
		cur = cur.right
	}
	reverseEdge(tail)
	return ans
}

func reverseEdge(from *TreeNode) *TreeNode {
	var pre *TreeNode
	var next *TreeNode
	for from != nil {
		next = from.right
		from.right = pre
		pre = from
		from = next
	}
	return pre
}

func findFirst(head, o1, o2 *TreeNode) *TreeNode {
	if head == nil {
		return nil
	}
	cur := head
	var mostRight *TreeNode
	var first *TreeNode
	for cur != nil {
		mostRight = cur.left
		if mostRight != nil {
			for mostRight.right != nil && mostRight.right != cur {
				mostRight = mostRight.right
			}
			if mostRight.right == nil {
				if first == nil && (cur == o1 || cur == o2) {
					first = cur
				}
				mostRight.right = cur
				cur = cur.left
				continue
			} else {
				mostRight.right = nil
			}
		} else {
			if first == nil && (cur == o1 || cur == o2) {
				first = cur
			}
		}
		cur = cur.right
	}
	return first
}

执行结果如下：

---

左神java代码