失配树学习笔记 | P5829 【模板】失配树

简介

失配树（简称 Fail 树），是基于 KMP 的算法，可以高效的解决复杂的字符串前缀后缀关系问题。

前置知识：

• KMP 算法（求失配数组）
• 最近公共祖先（LCA）

希望大家看完这篇文章后可以理解失配树。

引入

先来看一道题（校内模拟题·改）

给你一个字符串 \(S\)，你需要从它的非空前缀集合 \(\operatorname{Pre}\) 中选择一些字符串组成一个集合 \(Q\)，使得集合 \(Q\) 中任意两个字符串 \(A,B\)，\(A\) 不是 \(B\) 的后缀。求极大的集合 \(Q\)，输出 \(Q\) 中的所有字符串（可能有多组合法答案，输出其中任意一组）。

\(2 \leq |S| \leq 10^{6}\)

一个朴素的思路是，对于 \(\operatorname{Pre}\) 中的字符串，翻转后插入一个字典树中。最后找字典树的所有叶子节点即可。不难证明，这个算法是正确的。

可是这个算法是 \(O(n^2)\)的。无法通过本题。究其原因，是因为字典树中存在许多多余元素。比如字符串 abcdabghiab，建出来的字典树……

如何解决呢？我们可以考虑，跳过中间的多余元素。如何跳过？也就是说如何从 \(\operatorname{border}\) 指向包含它的字符串？当然是 \(\operatorname{KMP}\) 中的失配数组！于是我们自然的想到连边 \((\operatorname{nxt}_i,i)\)。然后找叶子。复杂度降到了 \(O(n)\)。

P5829 【模板】失配树

给定一个字符串 \(s\)，

有 \(m\) 组询问，每组询问给定 \(p,q\)，求 \(s\) 的 \(\boldsymbol{p}\) 前缀 和 \(\boldsymbol{q}\) 前缀 的 最长公共 \(\operatorname{border}\) 的长度。

\(1\leq p,q \le |s|\leq 10^6\)，\(1 \leq m \leq 10^5\)，\(s_i \in [\texttt{a}, \texttt{z}]\)

先建出失配树，对于第一个样例，失配树如下：

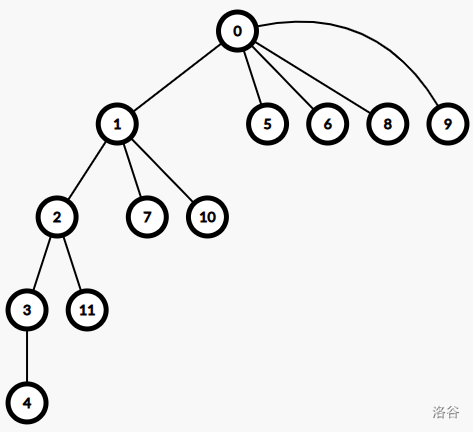
然后发现，最长公共前缀不就是在失配树上的最近公共祖先吗？

注意：

• 如果 \(\operatorname{LCA}(p,q) \in \{p,q\}\)，那么答案其实是 \(\operatorname{father}(\operatorname{LCA}(p,q))\)。
• 如果你使用的是树剖求 LCA，那么记住不能以 \(0\) 为根。

参考代码

#include <bits/stdc++.h>
#define int long long
using namespace std;

const int N = 1000005;

struct edge {
	int nxt, to;
} g[N << 1];
int head[N << 1], ec;
void add(int u, int v) {
	g[++ec].nxt = head[u];
	g[ec].to = v;
	head[u] = ec;
}

int root;
int siz[N], son[N], fa[N], top[N], dep[N];
void dfs1(int u, int father, int deep) {
	dep[u] = deep;
	siz[u] = 1;
	fa[u] = father;
	for (int i = head[u]; i >= 0; i = g[i].nxt) {
		int v = g[i].to;
		dfs1(v, u, deep + 1);
		siz[u] += siz[u];
		if (siz[v] >= siz[son[u]]) {
			son[u] = v;
		}
	}
}

void dfs2(int u, int father, int t) {
	top[u] = t;
	if (son[u])dfs2(son[u], u, t);
	for (int i = head[u]; i >= 0; i = g[i].nxt) {
		int v = g[i].to;
		if (v == son[u]) {
			continue;
		}
		dfs2(v, u, v);
	}
}

int lca(int x, int y) {
	int fx = top[x], fy = top[y];
	while (fx != fy) {
		if (dep[fx] < dep[fy]){
			swap(fx, fy);
			swap(x, y);
		}
		x = fa[fx], fx = top[x];
	}
	if (dep[x] > dep[y]) {
		return y;
	}
	else return x;
}

namespace KMP{
    int nxt[1000005];
    char s[1000005];
    int n;
    void kmp(){
        n = strlen(s+1);
        add(n+1,1);
        for(int i=2,j=0;i<=n;i++){
            while(j&&s[i]!=s[j+1]){
                j=nxt[j];
            }
            if(s[i]==s[j+1]){
                j++;
            }
            nxt[i]=j;
            if(j!=0){
                add(j,i);
            }
            else{
                add(n+1,i);
            }
        }
    }
}

int m;

signed main(){
    memset(head,-1,sizeof(head));
    ec=-1;
    cin>>(KMP::s+1)>>m;
    KMP::kmp();
    dfs1(KMP::n+1,0,1);
    dfs2(KMP::n+1,0,KMP::n+1);
    while(m--){
        int p,q;
        cin>>p>>q;
        int LCA = lca(p,q);
        if(LCA == p || LCA == q){
            LCA = fa[LCA];
        }
        if(LCA==(KMP::n+1))LCA=0;
        cout<<LCA<<'\n';
    }
    return 0;
}

AC Record