Codeforces 232 B Table 题解 [ 蓝 ] [ 分组背包 ] [ 组合数学 ] [ 循环节 ]

Codeforces 232B Table。

蒟蒻模拟赛上场切的一道蓝，非常难以置信我竟然能做蓝题。

这题的数据范围初看还是比较坑的，\(10^{18}\) 的值域很容易让人往矩阵加速那方面想。实际上在列出转移方程式后，我们发现状态是二维的，无法使用矩阵加速（或者说这样做很麻烦）。

思路

首先观察到每个边长为 \(n\) 的正方形的包含的点都一样，可以画出如下图：

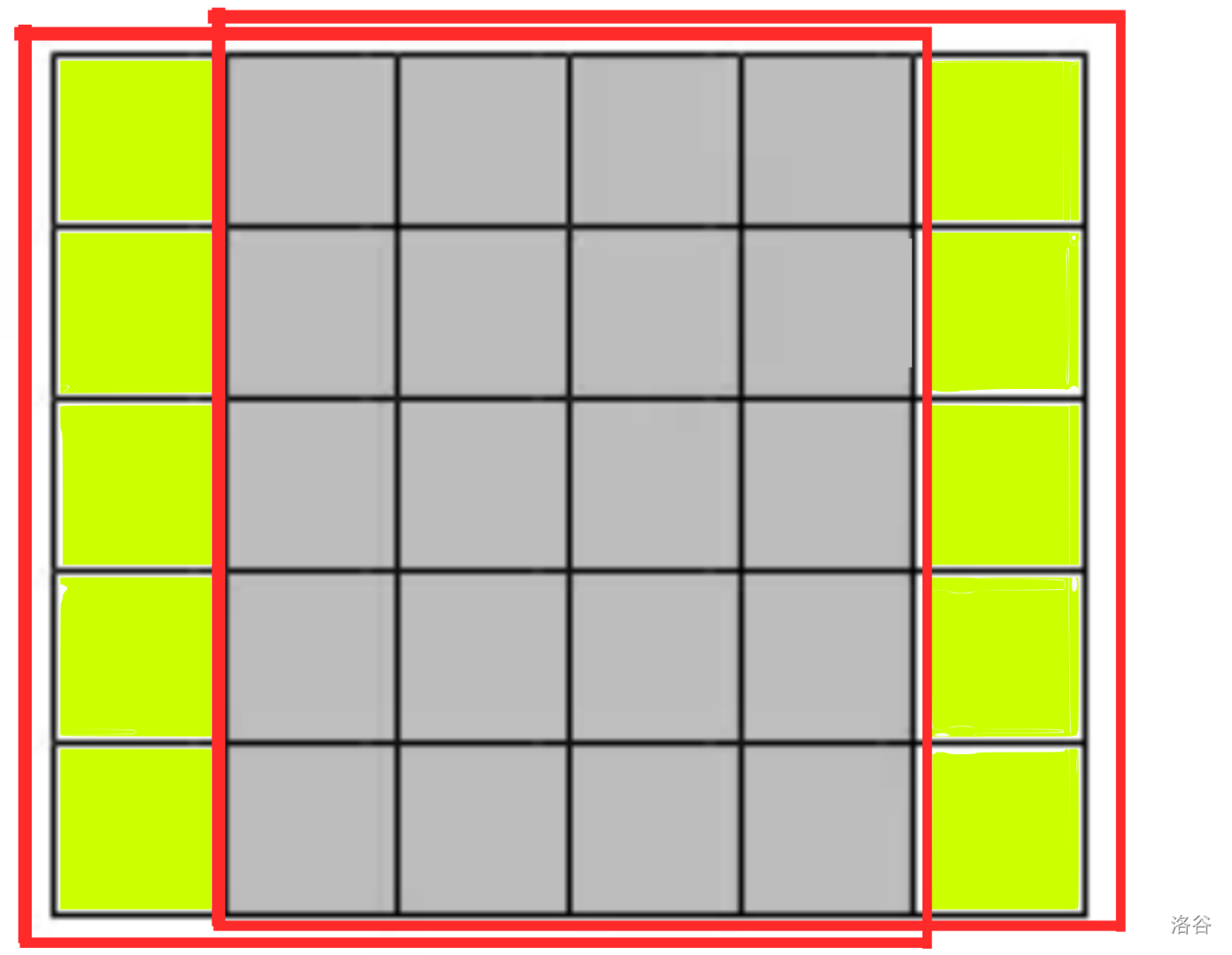
可以观察到：左边矩形与右边矩形重合的部分为中间灰色部分，它包含的点数记为 \(b\) ，左边黄绿色部分包含的点数记为 \(a\) ，右边黄绿色部分包含的点数记为 \(c\) 。

那么由题目条件可知：

\[a+b=b+c
\]

因此可得：

\[a=c
\]

所以我们可以发现，正方形每往后移动一位，移动前的第一列和移动后的最后一列的点数是一样的。

而本题求的是方案数，对于有 \(x\) 个点的一列，其方案数为 \(C_{n}^{x}\) 。并且又由于移动前的第一列和移动后的最后一列的点数一样，所以他们的方案数也一样。

如果我们把正方形每次的移动看做把第一列移动到最后一列接上，那么我们可以发现，正方形各列的点数形成了循环节。

于是对于正方形的每一列，我们把它看做一个类型，第 \(i\) 列的类型在整张棋盘中的出现次数则为 \(\left \lfloor \frac{m}{n} \right \rfloor\) ，如果 $ (m \bmod n) \ge i$ ，那么出现次数还会再加 \(1\) 。

接下来的问题就是求把 \(k\) 个点分给 \(n\) 个列，求出整个问题的总方案数了。

这是个很显然的分组背包，我们把每一列看做一个组，假设这一列在棋盘中出现了 \(y\) 次，按照放的点数 \(x\) 将列看做物品，其体积即为 \(x\) ，其贡献的方案数即为 \((C_{n}^{x})^y\) 。

正确时间复杂度为 \(O(n^2k)\) 。

注意优化常数，如果在转移过程中再计算快速幂和组合数那么会导致复杂度变成 \(O(n^2k\log n)\) ，于是我们需要预处理出这部分，才能保证复杂度正确。

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod=1e9+7;
ll n,m,k,ans=0,f[50005],g[50005],dp[50005],p[105][2];
ll qp(ll x,ll y)
{
	ll res=1;
	while(y)
	{
		if(y&1)res=res*x%mod;
		y>>=1;
		x=x*x%mod;
	}
	return res%mod;
}
ll niyuan(ll x)
{
	return qp(x,mod-2);
}
void init()
{
	f[0]=1;
	g[0]=1;
	for(int i=1;i<=10000;i++)
	{
		f[i]=f[i-1]*i%mod;
		g[i]=g[i-1]*niyuan(i)%mod;
	}
}
ll c(ll m,ll n)
{
	return 1ll*f[m]*g[m-n]%mod*g[n]%mod;
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	init();
	cin>>n>>m>>k;
	dp[0]=1;
	for(ll i=0;i<=n;i++)
	{
		p[i][0]=qp(c(n,i),m/n);
		p[i][1]=qp(c(n,i),m/n+1);
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=k;j>=0;j--)
		{
			int lmt=min(1ll*j,n);
			for(int l=1;l<=lmt;l++)
			{
				ll tmp;
				if((m%n)>=i)tmp=p[l][1];
				else tmp=p[l][0];
				dp[j]=(dp[j]+dp[j-l]*tmp%mod)%mod;
			}
		}
	}
	cout<<dp[k];
	return 0;
}