基于FATE的可验证秘密分享算法详解及应用场景分享：学习

内容来自“光大科技-基于FATE的可验证秘密分享算法详解及应用场景分享”

理论

基于Shamir的秘密共享方案，通过多项式插值实现。

加入可验证功能，即发送多项式系数的模数给对方作为承诺，对方通过分享值和承诺去进行验证！

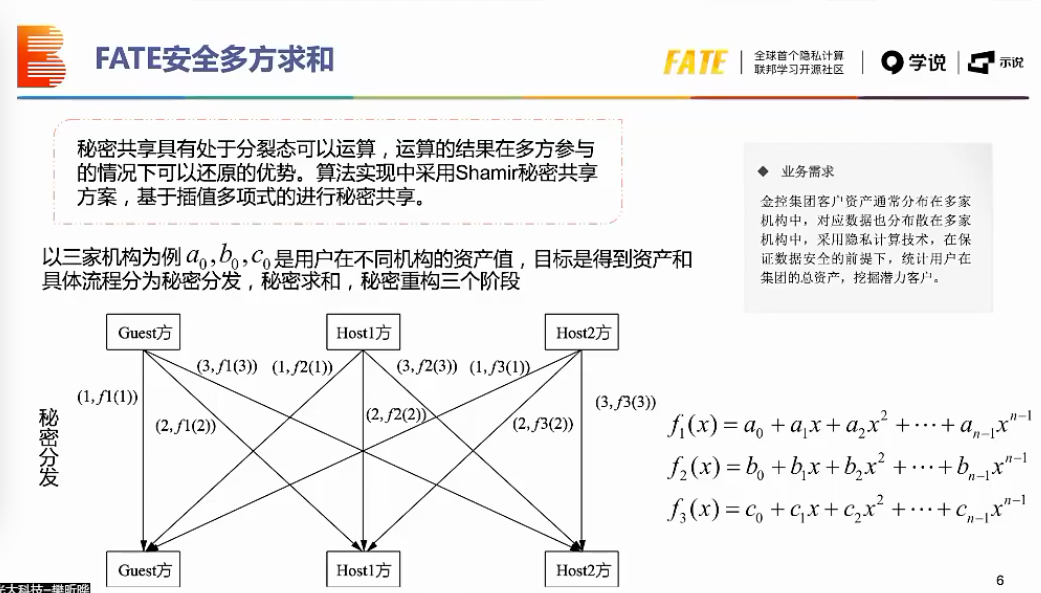
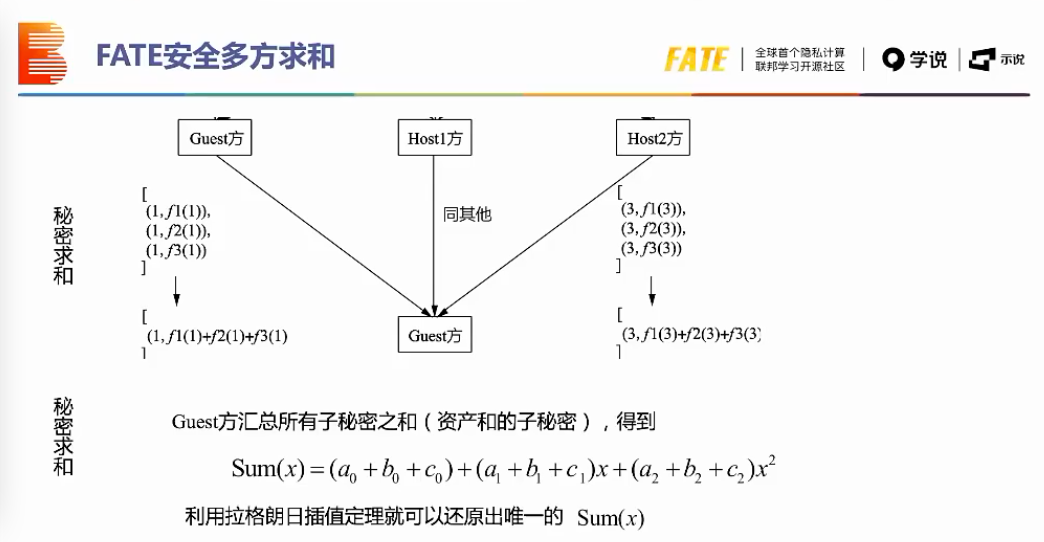
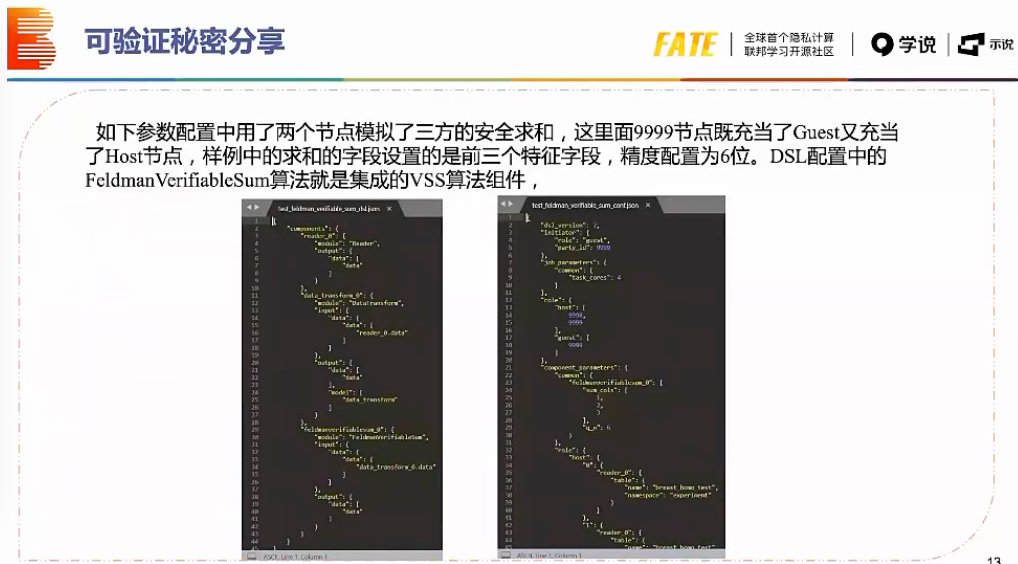
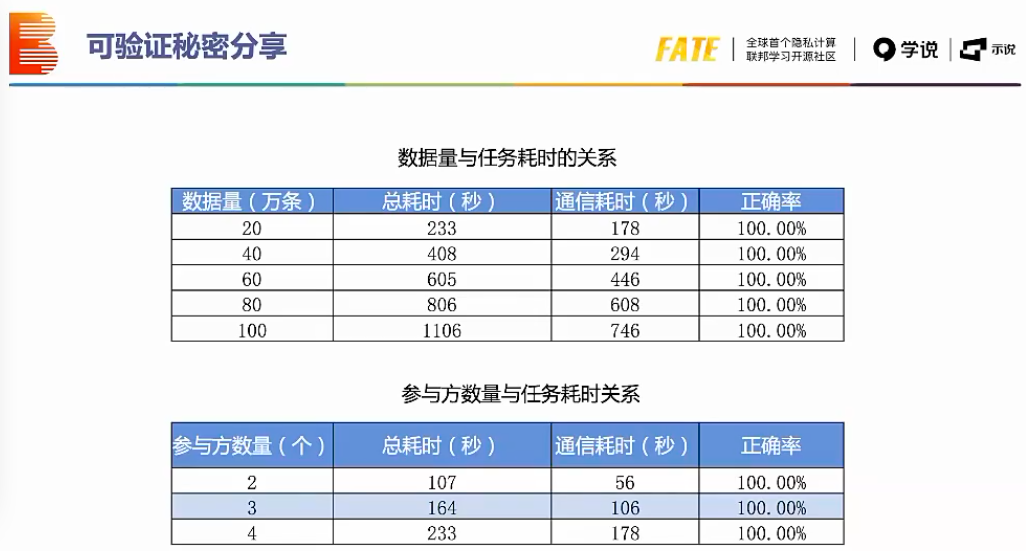
秘密共享

以下内容转载自“秘密共享—隐私计算和区块链共识中的榫卯”并加入一些自己的笔记。

什么是秘密共享？

秘密共享（Secret Sharing，SS）是1979年由Shamir和Blakey提出的，并在此之后40多年秘密共享被广泛认识和深入的研究。

秘密共享著名的(t，n)阈值方案如图1所示：



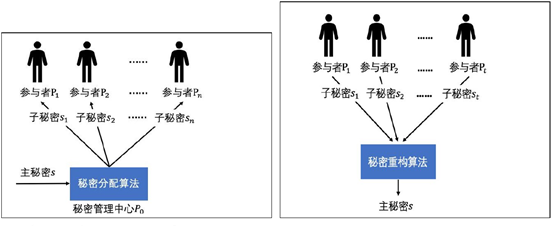
图1秘密分享的结构

秘密分享分为：分享和重构两部分：

设秘密\(s\)被分成\(n\)个部分，每一部分被称为一个子秘密并由一个持有者持有，并且大于等于\(t\)个参与者所持有的子秘密可以重构(Reconstruction)秘密\(s\)，而少于\(t\)个参与者所持有的子秘密无法重构秘密并且无法获得秘密\(s\)的任何信息。

实现方式

秘密共享方案的三种实现技术：

• 基于超平面几何的秘密共享，包括Blakley方案和Brickell方案；
• 基于插值多项式的秘密共享，包括经典的Shamir阈值秘密共享方案；
• Mignotte，Asmuth & Bloom提出的基于中国剩余定理的秘密共享；

基于中国剩余定理的秘密共享是在环上的运算，而Blakley & Brickell的超平面几何秘密共享方案和Shamir阈值秘密共享方案是在有限域上的运算，所以基于中国剩余定理的秘密共享和其他两个秘密共享的理论基础不尽一样。

Blakley和Brickell的超平面几何方案

来自【Blakley, G.R. Safeguarding cryptographic keys (PDF). in 1979 International Workshop on Managing Requirements Knowledge-1979】

1、Blakley的超平面几何分享

Blakley通过多维欧几里得空间来构造阈值秘密共享机制。任何\(t\)非平行\(t-1\)维超几何平面在一个t维空间中交于一点，秘密通过编码在坐标中完成秘密共享。如图3所示的三维欧几里得空间中的三个平面交于一点，秘密可以嵌入到交点的某一个坐标中。



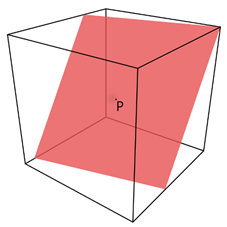
图2 秘密分发的2维超几何平面

Blakley方案的秘密分发和秘密重构过程如下：

（1）秘密分发

构造\(n\)个\(t\)维空间中的\(t-1\)维超几何平面分发给\(n\)个参与者，其中\(n>=t\)；图2是一个3维空间中的2维平面生成，一个秘密拥有者Dealer通过空间中的一个已知点\(P\)（秘密\(s\)是\(P\)的一个坐标值）的条件下生成任意多个过该点的平面。

（2）秘密重构

n个参与者中的t个参与者可以重构秘密s。如图3：任意3个参与者即可实现对共享点（包含秘密s）的重构，即三个非平行平面的交点。



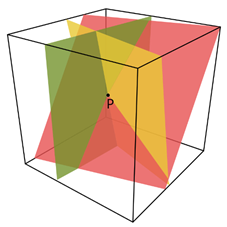
图3 三维欧几里得空间中的秘密重构

在秘密共享方案中，信息率是度量秘密共享方案安全性和效率的一个重要指标。所谓秘密共享的信息率可以简单理解为秘密的信息规模与每个子秘密的信息规模的比率。

Brickell的向量方法（矢量方法）相比于Blakley超平面几何的方法能够有效提高信息率。

2、Brickell的向量分享

Brickell的秘密共享方案采用向量方法，一个秘密拥有者Dealer把秘密\(s\)嵌入到一个向量中，再通过一个矩阵把秘密共享为\(n\)个子秘密分发给\(n\)个参与者，具体方法如下：

（1）秘密分发

选择秘密\(s\)和随机向量\((y2,y3, …… ,yt)\), 生成一个\(n*t\)矩阵\(M\)，\(M\)有\(n\)行，每行记为\(Mi\)，任意\(t\)个行向量都是线性无关的。秘密份额为\((s1，s2，……，sn)\)，每个份额是行向量\(Mi\)和列向量\((s,y2,y3, …… ,yt)\)的乘积。即\(si = Mi* (s,y2,y3, …… ,yt)\)

（2）秘密重构



其中\(M\)是一个公开参数，每行对应于一个参与者的子秘密\(si\)，任意\(t\)个参与者对应矩阵\(M\)的\(t\)个行向量，这\(t\)个向量组成一个\(t*t\)的方阵，根据前面的要求任意\(t\)个行向量线性无关所以此方阵满秩，所以可以有效的求解到\((ω1，ω2，……，ωt)\)使得：



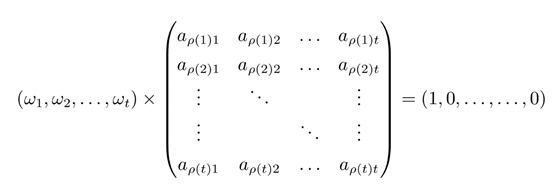
也就是任意\(t\)个\(M\)矩阵的行向量可以张成\((1,0,……,0)\)然后通过如下计算可以重构\(s\)：

Shamir的阈值秘密共享方案

来自【Shamir, A., how to share a secret. 1979】

Shamir秘密共享是目前应用最为广泛的阈值秘密共享技术，Shamir的方案的秘密分发和秘密重构过程如下：

（1）秘密分发

Dealer要共享一个秘密\(s\)，分给\(n\)个参与者，其中任意\(t\)个参与者可以重构秘密\(s\)，寻找一个\(t-1\)次多项式:



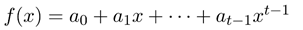
其中\(a_0=s\)，Dealer为每一个参与者任意选择非0的\(xi\)计算\(si=f(xi)\)，把\(si\)作为子秘密发送给参与者\(i\)。

（2）秘密重构

任何大于等于\(t\)个参与者通过其子秘密\(si\)和\(xi\)通过拉格朗日插值定理可以恢复上面多项式\(f(x)\)，并且令\(x=0\)实现秘密\(s\)的重构。

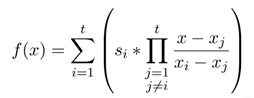
进一步对shamir秘密分享过程进行分析，可以发现在秘密分享阶段的计算：



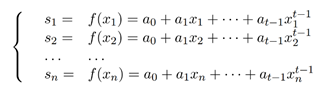
把以上的多项式用线性方程组的视角打开来看，是一个范德蒙德矩阵和一个列向量\((a0,a1……,at-1)\)乘积，其中范德蒙德矩阵和Brickell方案中的矩阵M是对应的。

因此，Shamir秘密共享是Blakley & Brickell方案中的特例，正因为范德蒙德矩阵的特殊性，线性无关性（\(xi\)不相等的任意\(t\)阶方阵都是满秩的）和构造简单，所以大多数方案应用Shamir秘密共享，如果需要把Shamir秘密秘密共享应用到一般模式可以考虑把范德蒙德矩阵用一般矩阵替代。

基于中国剩余定理的秘密共享

什么是中国剩余定理（CRT）？

物不知数问题：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

CRT：



使用CRT解“物不知数问题”：

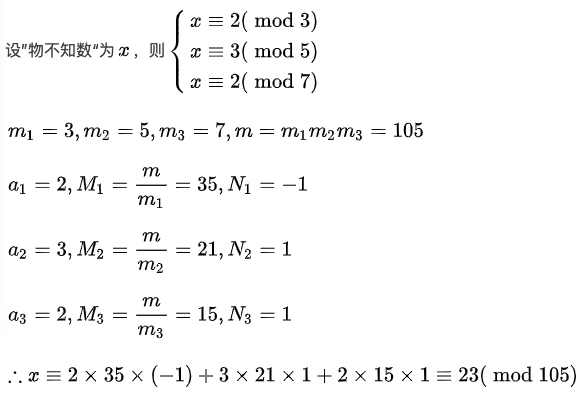
基于CRT的秘密共享：

举例：

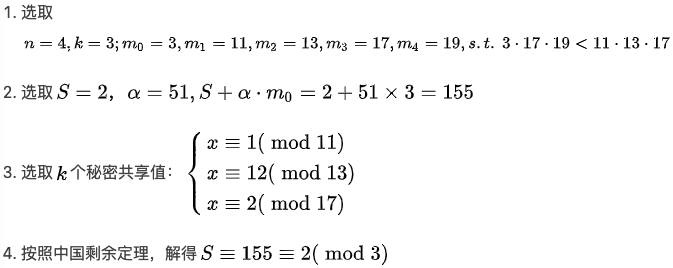
可验证的秘密共享

在秘密共享中，为了解决参与者想验证Dealer是否欺骗自己以及Dealer如何证明自己没有欺骗参与者的问题，提出了可验证的秘密共享（Verifiable Secret Sharing，VSS），Feldman VSS 是一种基于Shamir秘密共享构造的可验证秘密共享方案。

（1）秘密分发

Dealer要共享一个秘密\(s\)，分给\(n\)个参与者，其中任意\(t\)个参与者可以重构秘密\(s\)，寻找一个\(t-1\)次多项式，

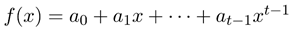
其中\(a_0=s\)，Dearler为每一个参与者任意选择非0的\(xi\)计算\(si=f(xi)\)为\(i\)的子秘密发送给参与者\(i\).同时，Dealer计算\(A_j=g^{a_j}\),其中\(j=0，1，2……，t-1\)并公开这些参数。

（2）秘密验证

参与者收到秘密\(si\)后验证\(si\)的有效性，即通过验证以下等式是否成立：



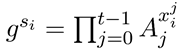
其中\(A_j=g^{a_j}\) .

补充

分布式可验证秘密共享

在以上所有的方案中Dealer是一个知道秘密的实体。Joint Feldman VSS方案既能实现上述的可验证的秘密共享又能去掉Dealer，即一种无可信第三方的可验证秘密共享方案（Distributed Verifiable Secret Sharing，DVSS）

具体过程如下：

（1）秘密分发

每一个参与者Pi选择要共享的秘密\(si=a_0\)并随机选择其他参数生成\(t-1\)次多项式：

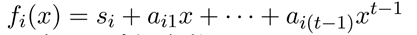
公开参数\(A_{ik}\)并公布，对每一参与者\(P_j\)生成秘密\(si\)的子秘密\(s_{ij}=f_i(x_j)\)，将\(s_{ij}\)发送给参与者\(P_j\).

（2）秘密验证

每一个参与者可以验证其他参与者发送给自己的秘密是否有效，并把所有验证通过的参与者记为集合\(Q\)；

所有参与者把秘密分享验证通过集合\(Q\)内的子秘密进行加运算就得到该参与者的子秘密\(si\).

问题：如何验证秘密有效？

联邦学习的应用

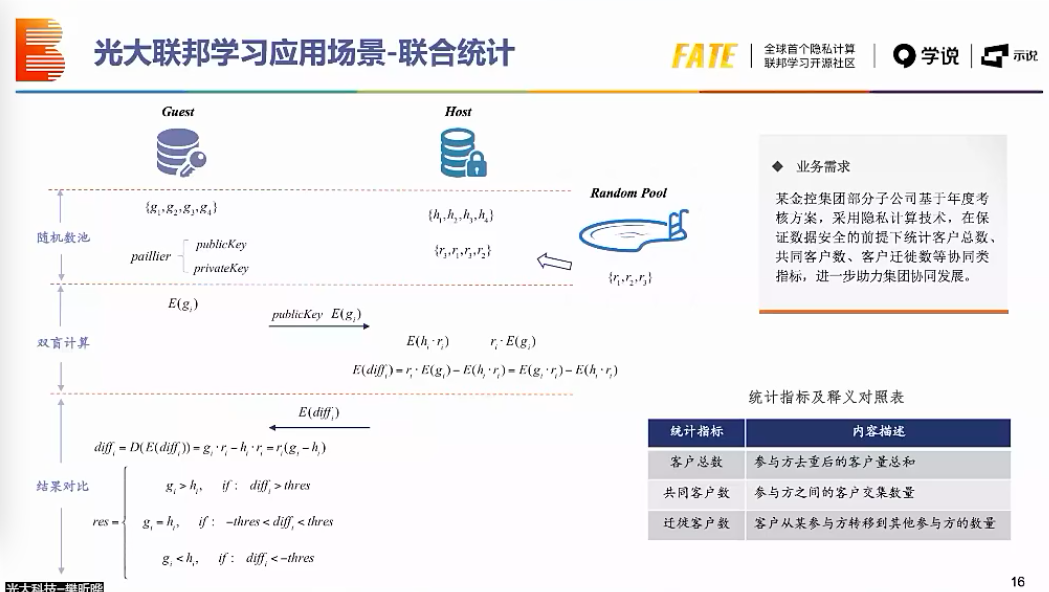
这里用到Paillier加法同态性怪怪的。

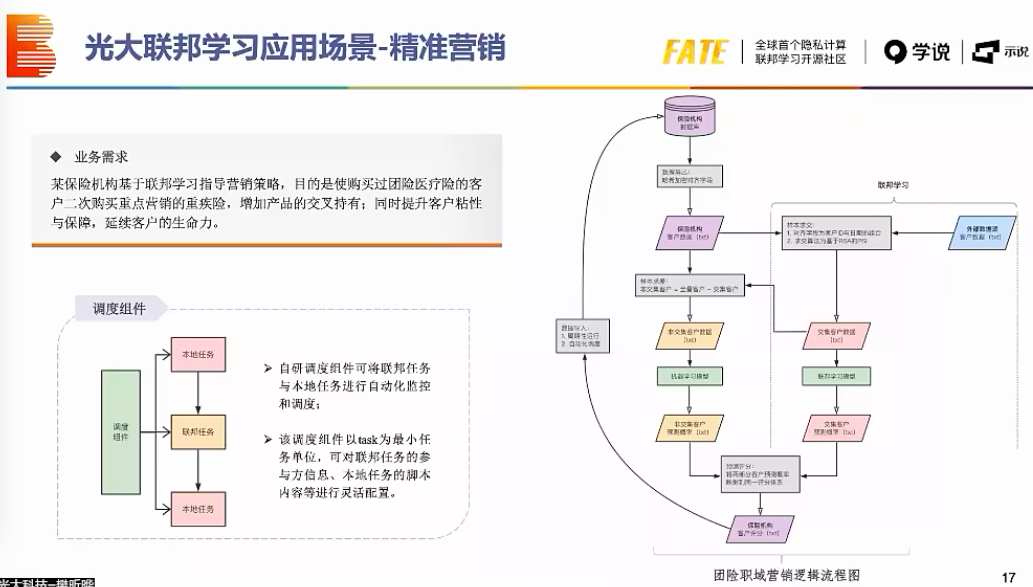
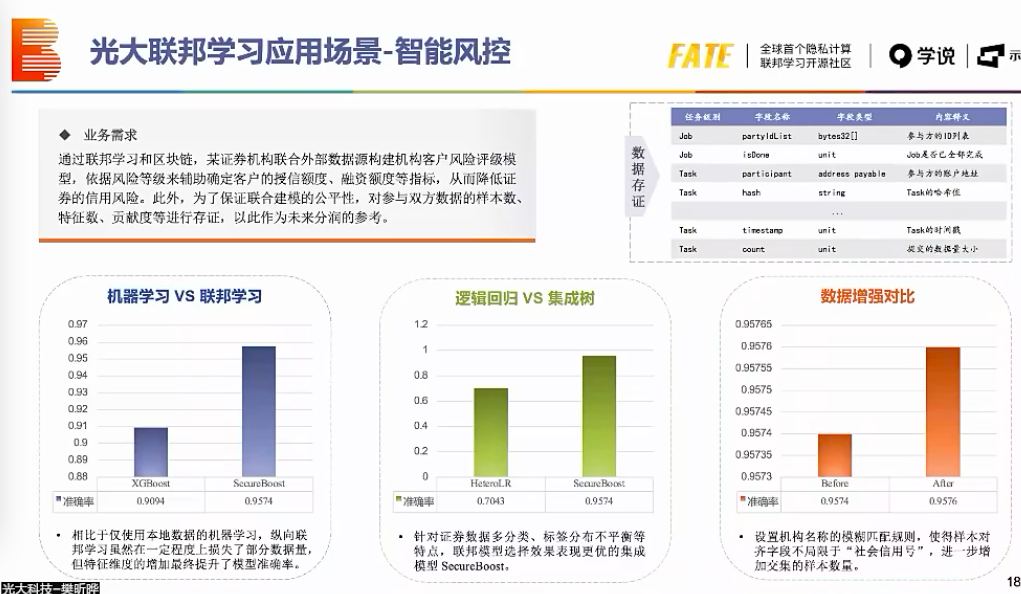
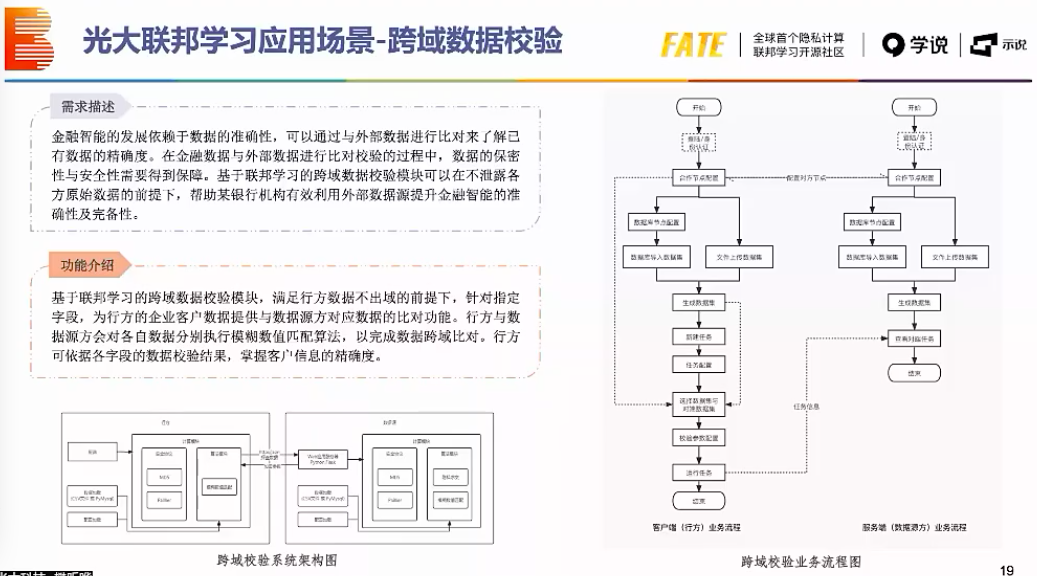
在区块链共识和隐私保护中的应用

被称为革命性的第三代加密货币的Cardano（ADA）的共识算法Ouroboros和致力于利用区块链打造一款具备无限扩容能力的自治分布式云计算网络项目Dfinity中的共识算法都不约而同的选择了分布式可验证的秘密共享技术。在信任环境、分布式结构上，区块链的共识节点和分布式可验证秘密的参与者都恰分的对应，这样分布式可验证秘密共享的特征在区块链共识中得到充分的展现，能恰到好处的解决区块链共识算法的吞吐率和资源浪费的问题。

在日趋严格的隐私保护政策下，各种隐私保护算法被提出，其中联邦学习和共享学习最为突出，其内部的安全层都有采用了秘密共享技术实现隐私保护的技术方案。在联邦学习中，基于秘密共享的逻辑回归模型中利用了秘密共享的加法同态性，数据拥有者将秘密共享给多方，在秘密共享的场景下，将明文的计算转换为子秘密的计算，实现了隐私保护，蚂蚁金服的共享学习框架中也采用秘密共享技术作为隐私保护实现的技术之一。

参考

1、Shamir密钥分享算法简析

2、基于中国剩余定理的秘密共享