Solution Set - “说选个晴日，露能滴出彩虹”

0.「BZOJ #3457」Ring
1.「CF 1824C」LuoTianyi and XOR-Tree
2.「CF 1824D」LuoTianyi and the Function
3.「CF 1728F」Fishermen
4.「CF 1305H」Kuroni the Private Tutor
5.「十二省联考 2019」「洛谷 P5291」希望
6.「IOI 2007」「洛谷 P4649」训练路径
7.「BJOI 2018」「洛谷 P4429」染色
8.「AHOI/HNOI 2017」「洛谷 P3725」队长快跑
9.「LOJ #6261」一个人的高三楼
10.「CF 1408I」Bitwise Magic
11.「NOI Simu.」图腾
12.「NOI Simu.」糖果
13.「ARC 160A」Reverse and Count
14.「ARC 160B」Triple Pair
15.「ARC 160C」Power Up

\[\mathfrak{Defining~\LaTeX~macros\dots}
\newcommand{\son}[0]{\operatorname{son}}
\newcommand{\high}[0]{\operatorname{high}}
\newcommand{\floor}[1]{\left\lfloor#1\right\rfloor}
\]

0.「BZOJ #3457」Ring

Private link & Submission.
「A.数学-Pólya 计数」「B.向量-矩阵优化」

Pólya 不如 Burnside, 在初等的题目上相信这一点. (

Burnside 嘛, 设当前枚举的循环节长度为 $\ell$, 关键问题在于算出有多少个长度为 $\ell$ 的串, 其循环同构串中 $S$ 作为子串出现过. 对循环节增量枚举的过程显然是 $S$ 的匹配自动机上结点的线性变换, 用矩阵快速幂计算即可. 注意这里需要钦定末尾的匹配状态, 转完一圈后再用的确达到这个状态的方案贡献答案. 为了避免增大矩阵大小, 可以容斥算非法方案. 不过复杂度都是 $\mathcal O(d(n)k^3\log n)$ 的.

1.「CF 1824C」LuoTianyi and XOR-Tree

Link & Submission.

显然, 树合法的必要条件是对于每个 $u$, $u$ 到子树内叶子的距离相等. 注意若我们在处理 $u$ 子树外的结点时, 对 $u$ 内的距离提出了某种要求, 我们至少可以通过修改 $a_u$ 在一步额外操作内满足要求. 因此, 我们只需要保留最小化 $u$ 子树内的代价的决策, 其余的决策都不如在被保留的决策基础上直接修改 $a_u$ 来得快.

于是, $u$ 子树的信息就是一个可选的最优距离集合 $S_u$. 合并子树时, 就是将所有集合合并, 取出出现次数最多的元素组成新的集合. 这一过程可以用 Trie 或者启发式合并维护, 但都难以避免麻烦的时间戳标记. 一个好写的算法是: 用 map 维护, 启发式合并 $S_u$ 后, 若最大出现次数 $>1$, 则暴力扫描 $S_u$ 删除所有不需要的元素. 这样好写不少, 只扫描被合并入大集合的元素也能保证 $\mathcal O(n\log^2n)$ 的复杂度.

2.「CF 1824D」LuoTianyi and the Function

Link & Submission.

没题出可以咬打火机喵~

对右端点扫描线, 线段树维护历史和就行. 维护 $3\times3$ 矩阵中的 $6$ 个位置, 稍微写精细一点就稳过了. 复杂度 $\mathcal O((n+q)\log n)$.

3.「CF 1728F」Fishermen

Link & Submission.
「A.图论-网络流-费用流」「B.Tricks」

有一个显然但 $\mathcal O(\text{MCF}(n^2,n^2))$ 的费用流大暴力, 我们可以尝试模拟费用流.

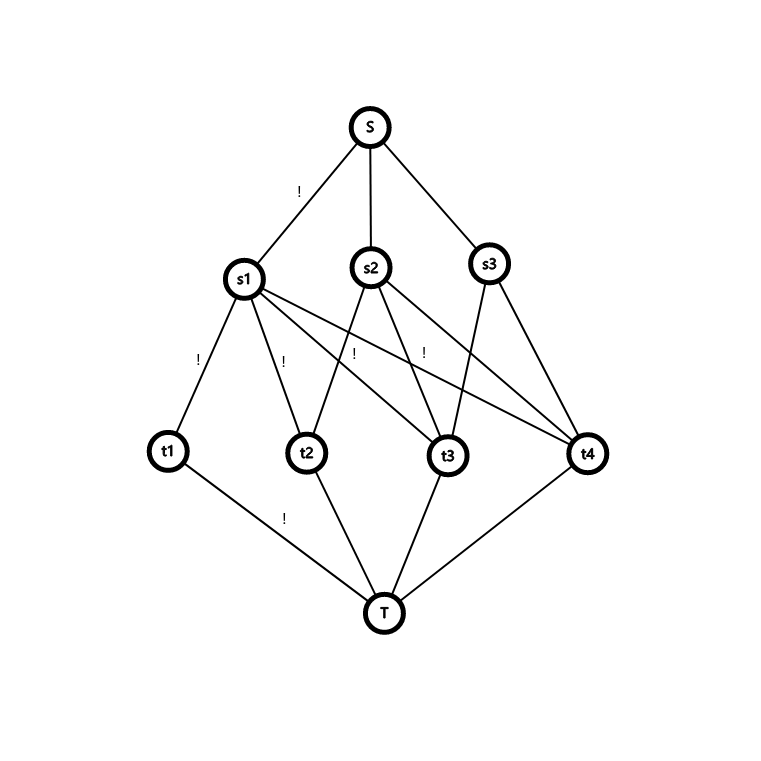
例如, 我们从大到小加入元素对应的点, 那么就有两种可能的负环: $S\to s_1\to t\to s\to \cdots\to t\to T$, 以及 $s_1\to t\to \cdots\to T\to\cdots\to s$. 后面这种环可以通过顺序加入 $t$ 而非 $s$ 规避掉, 此时暴力用匈牙利增广前面一种环即可. 复杂度 $\mathcal O(n^3)$.

4.「CF 1305H」Kuroni the Private Tutor

Link & Submission.
「A.图论-网络流-最大流/最小割」「B.贪心」「C.性质/结论」「C.思维」

假设已知 $\{s_m\}$, 如何判断分数安排的合法性呢? 虽然可能有些浪费, 但流网络显然能够很好地描述 "把分数分配给学生" 的情景. 我们可以给出这样的流网络:

\[\begin{aligned}
V &= \{S,T\}\cup\{x_n\}\cup\{y_m\},\\
E &= \{\lang S,x_i,[l_i,r_i]\rang\mid i\in[1,n]\}\\
&\cup \{\lang x_i,y_j,[0,1]\rang\mid i\in[1,n],j\in[1,m]\}\\
&\cup \{\lang y_i,T,[0,s_i]\rang\mid i\in[1,n]\}.
\end{aligned}
\]

若 $G=(V,E)$ 存在从 $S$ 到 $T$, 流量为 $f=t=\sum_is_i$ 的可行流, 那么安排方案就合法. 而显然 $f\le t$, 所以这也可以描述为 $f\ge t$, 即所有 $G$ 上的割至少为 $t$.

先考虑上界, 设割集为 $(A\mid B)$, 那么:

\[\sum_{i\in X_B}r_i+|X_A|\cdot|Y_B|+\sum_{i\in Y_A}s_i\ge t.
\]

显然, 为了取出最小化的割来缩紧限制, 我们可以令 $\{r_n\}$, $\{s_m\}$ 降序排列, 那么:

\[\forall a\in[0,m],~\forall b\in[0,n],~\sum_{i>a}r_i+\sum_{i>b} s_i+ab\ge t.
\]

考虑下界, 类似于上下界网络流的一贯手法, 我们研究提供下界流量的 $S'$, 它的所有出边全部满流, 于是 $S,S'$ 不属于同一个割. 则当 $S\in B$, $S'\in A$ 时:

\[\sum_{i\in X_B}l_i+|X_A|\cdot|Y_B|+\sum_{i\in Y_A}s_i\ge\sum_{i=1}^nl_i.
\]

当 $S\in A$, $S'\in B$ 时:

\[\sum_{i=1}^nl_i+\sum_{i\in X_B}r_i+|X_A|\cdot|Y_B|+\sum_{i\in Y_A}s_i\ge t.
\]

后者是第一个式子的必要, 就不用考虑了. 前者也可以通过排序权值化简. 最终得到判据

\[\forall a,b,~ab+\sum_{i>b}s_i\ge\max\left(t-\sum_{i>a}r_i,\sum_{i\le a}l_i\right).
\]

右式和 $b$ 无关, 而左侧 $\{s_m\}$ 已经单调, 因此枚举 $a$ 时, $b$ 的移动也是单调的, 借此可以快速判定.

接下来, 显然并列人数可二分, 设并列人数为 $w$, 我们需要贪心地安排一个 "最容易合法" 的 $\{s_m\}$, 根据判据, 我们就需要让 $s$ 的后缀尽量大, 也就是尽可能平均. 从后往前扫每段有上界的区间, 不断让它们整体增加即可. 前 $w$ 的值也可以二分地钦定. 这样一次检查是线性的, 最终复杂度 $\mathcal O((n+m)(\log n+\log m))$.

5.「十二省联考 2019」「洛谷 P5291」希望

Link & Submission.
「A.树论-长链剖分」「B.Tricks」

也不能说很难想吧… 反正代码是贺的 (骄傲.jpg).

我们希望枚举目标发动机 $u$, 然后再来计算可行的集合方案, 但这样会算重. 不过, 当集合方案一定时, 可行的 $u$ 点一定构成连通块, 于是我们可以通过 "连通块数 (合法集合方案数)" = "点数 (对于 $u$ 点合法的方案数)" - "边数 (对于两个端点都合法的方案数)" 来完成容斥.

接下来就是树 DP 嘛. 令 $f(u,\ell)$ 表示仅考虑 $u$ 子树内的点, 组成到 $u$ 距离不超过 $\ell$ 的连通块数量 (含空集), $g(u,\ell)$ 表示仅考虑 $u$ 子树外的点, 组成到 $u$ 距离不超过 $\ell$ 的连通块数量 (含空集), 设 $x$ 是 $u$ 的父亲, 那么

\[f(u,\ell)=\prod_{v\in\son(u)}f(v,\ell-1)+1,\\
g(u,\ell)=g(x,\ell-1)\prod_{v\in\son(x)\setminus\{u\}}f(v,\ell-2)+1.
\]

这个 $f$ 倒是可以长剖求, 不过也需要很痛苦的乘法和加法标记维护. 对于 $g$, 这个 $\ell$ 的上界是子树外最远距离, 可以用类似 "反向长剖" 的方式得到维护思路: 从父亲向重儿子遗传信息, 每次指针向前移动而非正常长剖的向后移动. 注意这里内存池理论上只需要维护距离的一段后缀, 也和正常长剖有所区别. 对于 $v\in\son(x)\setminus\{u\}$, 我们可以在求 $g$ 的时候维护乘积前缀, 同时将对 $f(v,\cdot)$ 对 $f(u,\cdot)$ 的所有更新全部撤销, 这样就规避了持久化数据结构. 线性求逆元可以做到线性, 当然这里放一个 $\mathcal O(n\log P)$ 也是能过的.

6.「IOI 2007」「洛谷 P4649」训练路径

Link & Submission.
「A.DP-树上 DP」「C.性质/结论」

终于能做道紫题了…

我们可以容忍奇环的存在, 但注意到若两个奇环边有交, 则一定可以生成一个非法的偶环. 所以, 最后得到的图一定是一个不包含偶环的仙人掌.

考虑树 DP, 在 LCA 处决策非树边的贡献. 设 $f(u)$ 表示仅考虑 $u$ 子树内部的点和边, 最多能保留的非树边边权和, 特别地, 因为我们在加入 LCA 时要求路径上的边不被其他非树边跨过, 我们还需要处理 $f(u,v)~(v\in\son(u))$, 表示 $u$ 子树除去 $v$ 子树后, 其余部分的贡献. 到此, 非树边 $(x,y)$ 的贡献就可以描述为

\[\sum_{t\in(x\to y)\setminus\{u\}}f(t,\text{pre}(t)),
\]

其中 $\text{pre}(t)$ 即爬树过程中的上一个结点. $(x,y)$ 参与贡献时, 还需要保证爬到的至多两个 $u$ 的儿子不被其他非树边占据, 因此在 $u$ 处还需要记录集合状态 $g_u(S)$ 来辅助转移. 其他的小细节就不提啦, 复杂度 $\mathcal O(m2^k)$, 其中已知有 $k=10$.

7.「BJOI 2018」「洛谷 P4429」染色

Link & Submission.
「C.性质/结论」

第一眼: 奇环无解.

第二眼: 若一个换上的点颜色被强制确定, 可以构造方案让环非法. 也就是说, 有能力钦定环上一个点的颜色. 所以若存在两个边不交环就无解.

此外, 一个环显然有解. 所以我们需要研究的还剩下两个相交环的情况. 此时, 在拓扑去掉树状分枝后, 图一定长成这样:

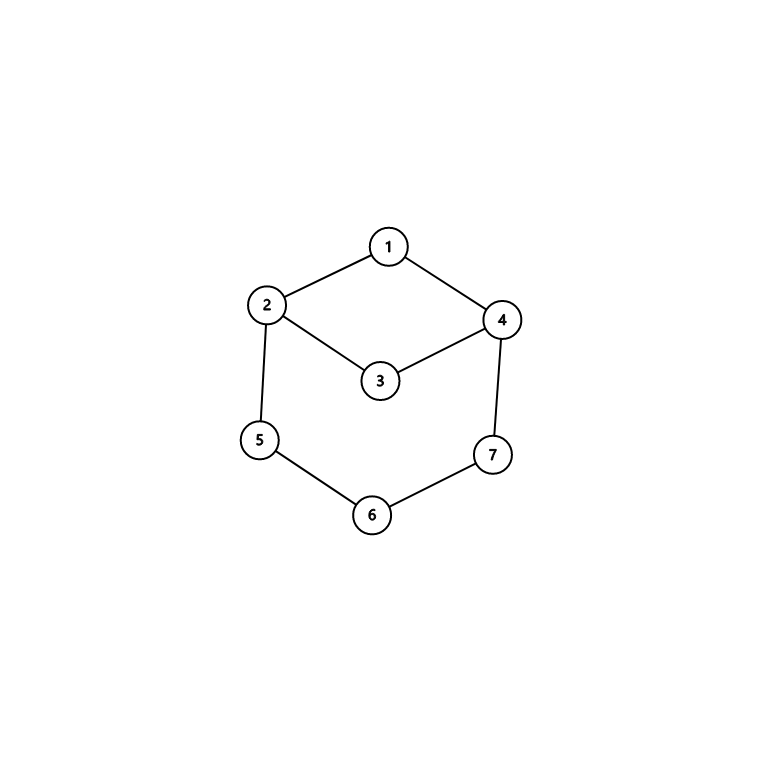
我们关注唯二的三度点. 这样的图并非一定合法, 例如说:

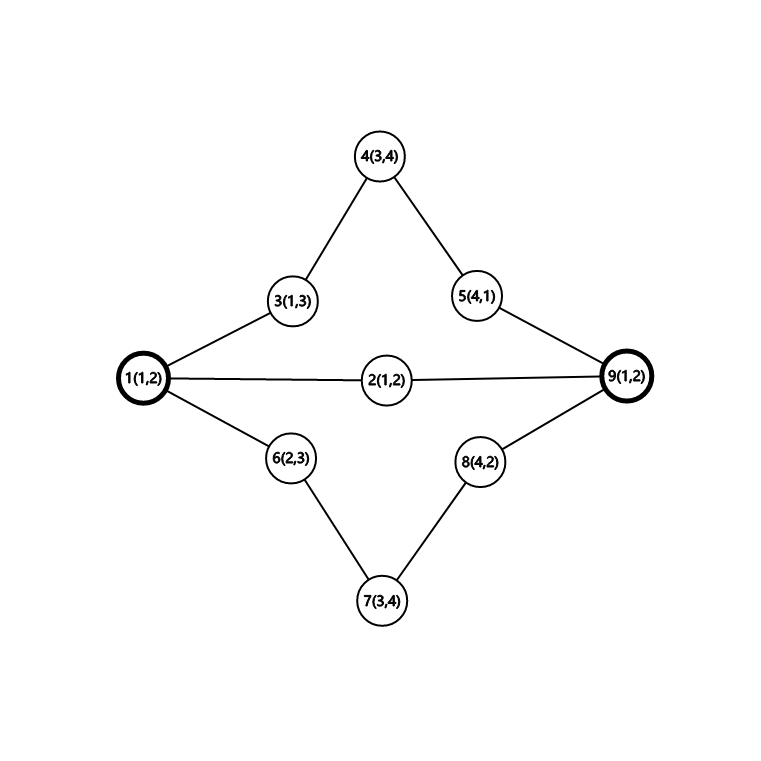
和环上 "钦定值" 的构造类似, 我们用路径 $1\to2\to9$ 描述 "$1$ 与 $9$ 同色", 用 $1\to3\to4\to5$ 描述 "$1$ 若选 $1$, $9$ 只能选 $2$", 用 $1\to6\to7\to8\to9$ 描述 "$1$ 若选 $2$, $9$ 只能选 $1$", 后两条路径组合出 "$1$ 与 $9$ 异色", 矛盾就产生了.

这样的构造在含有至少两条长度至少为 $4$ 的链时都奏效, 其余的小情况可以手玩. 最后我们得到结论: 两个三度点需要同时邻接至少两个点才有解.

In conclusion, 一个图有解, 当且仅当其是二分图; 拓扑消除树结构后, 每个连通块中不存在两个以上的环或者存在恰好两个环, 且两个环的三度点同时邻接至少两个点. 后面这句复杂的话还能简化成: 不存在度数 $\ge4$ 的点, 至多存在两个度数 $=3$ 且它们同时邻接至少两个点. 随便判判就行, $\mathcal O(n+m)$.

8.「AHOI/HNOI 2017」「洛谷 P3725」队长快跑

Link & Submission.
「A.计算几何」「C.性质/结论」

显然我们仅会经过起点, 终点和机关的发射点. 不过欧式距离看上去就不可维护, $10^6$ 的点数也几乎没法优化建图, 所以这里一定得有结论!

首先, 我们其实不太关心射线的具体方向, 因为保证有解, 我们只需要知道能不能从一个发射点的下方/上方走到终点. 在一定讨论后, 所有射线都可以转化到竖直方向.

接下来, 我们先来考虑只有一种方向的射线的情况, 如图 (是薅的, 下同):

若只有向上的射线, 我们的行走路径一定是一个下凸壳. 同理, 若只有向下的射线, 我们的行走路径一定是一个上凸壳.

然后, 考虑不同方向的射线的相互影响, 如图:

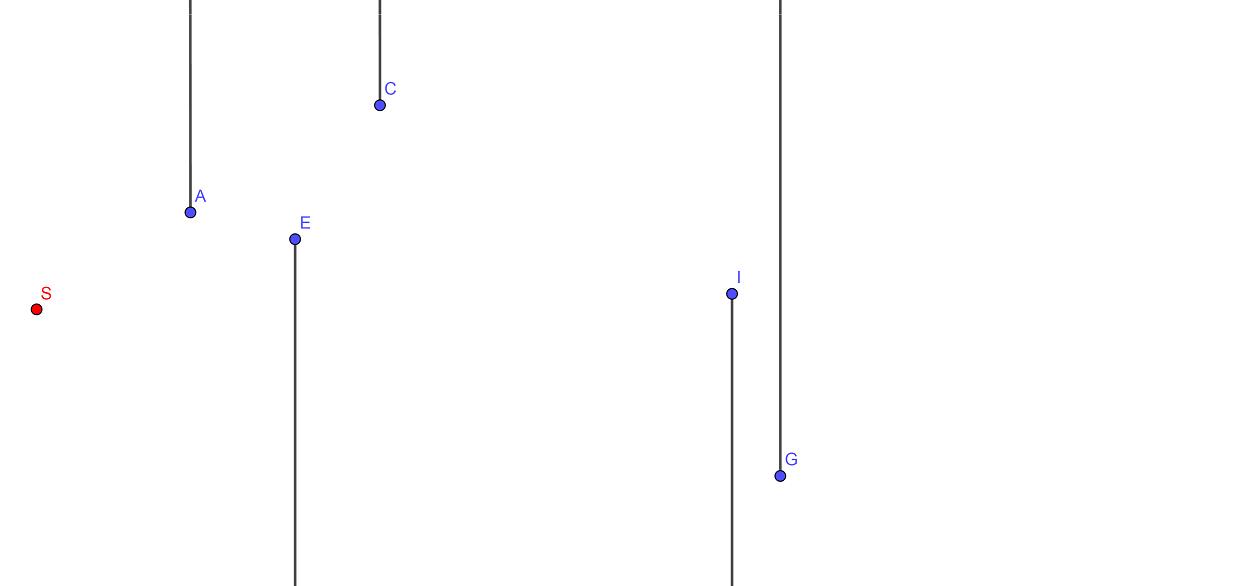
其中 $S$ 是当前已确定路径的端点, 注意 $CG$ 被 $\ell_I$ 截断, 那么此时 $SG$ 一定被当前最左侧向下的射线 $\ell_E$ 截断. 此时清空同向凸包, 保留反方向凸包上的第一个能连接 $G$ 的点加入同向凸包即可. 感性是优秀的. (哭哭

复杂度 $\mathcal O(n\log n)$, 瓶颈是排序.

9.「LOJ #6261」一个人的高三楼

Link & Submission.

萌萌题乱入是怎么回事… 算 $F(z)/(1-z)^k$ 就行, $\mathcal O(n\log n)$.

10.「CF 1408I」Bitwise Magic

Link & Submission.
「A.数学-FWT」「B.Tricks」

不难得到:

\[F_i(x,y)=\sum_{j=0}^k\frac{x^j}{j!}y^{a_i-j},\\
\textit{ans}=k![x^k]\prod_{i=1}^nF_i(x,y).
\]

其中 $F_i(x,y)$ 在 $x$ 维加法卷积, 在 $y$ 维异或卷积. 这里应该是比较初等的.

接下来我们需要计算这个卷积结果. 因为 $k\le16$, 加法卷积部分也没什么可观的大优化, 所以核心自然是处理异或卷积的部分. 第一个观察自然是每个 $F_i(x,y)$ 的项数都很小, FWT 可以手动进行, 但 FWT 得到的向量一共都有 $2^{16}\times2^{16}$ 个多项式, 我们还得把它们乘乘加加, 这怎么可能?

因此, 这里的 key motivation 是, 我们猜测这个问题严格弱于对稀疏多项式的卷积. 弱在哪里? $y$ 的指数是连续的!

连续的自然数, 它们的高位几乎都是相同的, 如果我们把 $F_i(x,y)$ 按照 $t=\high(a_i\oplus (a_i-k))$ 归类, 则 $t$ 相同的一类中的卷积实际上只需要做 $[0,2^{t+1})$ 上的卷积, 更高的位一定是所有数直接异或出来的结果. 卷积部分, 我们沿用稀疏多项式的做法, 手动 FWT 然后对 $x$ 维做暴力加法卷积, 卷完之后就剩下 $c$ 个向量, 我们再把每个向量扩充到 $[0,2^c-1)$, 全部卷起来, 最后 IFWT 一次就能得到答案.

$c$ 个向量的暴力卷积复杂度是 $\mathcal O(ck^22^c)$, 前面手动 FWT 运算次数打表出来最坏是 $1.6\times10^9$ 量级. 本地极限数据 $3.8\text s$, 这… 兔的常数也太小了.

嘛, 其实正解做法和这个也差不多, 把多项式指数 $y^{a_i-j}$ 全部换成 $y^{a_i\oplus(a_i-j)}$, 这样本质不同的 $F$ 约有 $200$ 个, 每一类单独处理然后快速幂乘起来就行. 其实复杂度算出来也没优秀多少是不是. (

11.「NOI Simu.」图腾

Private link & Submission.

不难发现相邻两个点只有一维坐标相差 $1$, 又因为起点坐标全是偶数, 所以每次只能将一个偶数 $\pm1$ 得到下一个坐标. 可能的后继方案形成了一个 DAG, 建虚点求它的最小割即可. 复杂度 $\mathcal O(\text{Dinic}(n,nk))$, 因为答案不超过 $n/k$ 所以有上界 $\mathcal O(n^2)$.

12.「NOI Simu.」糖果

Private link | 口胡力!
「A.构造」

首先, 由于总和的奇偶性不变, 所以 $n\equiv2\pmod4$ 时无解. 如果以过题为目的, 下一步应当是思考答案下界. 因为一个连通块中我们一定是操作出一个树形结构, 所以总操作次数不少于 $n-$ 连通块个数. 同时, 最多只有一个单点连通块, 且不存在大小为 $2$ 的连通块, 所以至多 $\floor{\frac{n-1}{3}}$ 个连通块, 进而操作次数至少为 $\floor{\frac{2n}{3}}$.

有目标了, 来构造叭!

第一个 motivation: 我们可以找一些优秀的 pattern. 对于一列 $(x,y,z)$, 我们可以用两次操作将它们变为三个 $x-y+z$; 对于一列 $(a,a+1,a+3,a+2)$, 我们可以用三次操作将它们变为任意的同一个数 (这也对应部分分的构造). 如果我们可以将 $1\sim n$ 划分入这样的三元组, 使得每组的 $x-y+z$ 都相同 (最多单出一个 $x-y+z$), 剩下一些常数部分用四元组扫尾, 就完成构造了.

抄抄题解.

$n=12k+3$, $x-y+z=6k+2$:

\[\begin{array}{ccc|c}
i & 4k+2i+1 & 10k+i+3 & i\in[1,k]\\
k+i & 6k+2i+1 & 11k+i+3 & i\in[1,k]\\
2k+i & 4k+2i & 8k+i+2 & i\in[1,k]\\
3k+i+1 & 6k+2i+2 & 9k+i+3 & i\in[1,k]\\
3k+1 & 6k+2 & 9k+3
\end{array}
\]
$n=12k+4$: 在 $n=12k+3$ 的基础上, 最后一组替换为 $(3k+1,9k+3,12k+4)$, $6k+2$ 单列.
$n=12k+8$: 在 $n=12k+4$ 的基础上, 用四元组处理最后四个数.
$n=12k+12$: 在 $n=12k+8$ 的基础上, 用四元组处理最后四个数.
$n=12k+1$, $x-y+z=6k+1$:

\[\begin{array}{ccc|c}
i & 2k-i+1 & 8k-2i+2 & i\in[1,k]\\
2k+i & 4k-i+2 & 8k-2i+3 & i\in[1,k]\\
6k-2i+1 & 11k-i+2 & 11k+i+2 & i\in[1,k)\\
6k-2i+2 & 9k-i+3 & 9k+i+2 & i\in[1,k]\\
3k+1 & 8k+2 & 11k+2\\
/ & 6k+1 & /
\end{array}
\]
$n=12k+5$: 在 $n=12k+1$ 的基础上, 用四元组处理最后四个数.
$n=12k+9$: 在 $n=12k+5$ 的基础上, 用四元组处理最后四个数.
$n=12k+7$, $x-y+z=6k+4$:

\[\begin{array}{ccc|c}
i & 2k-i+3 & 8k-2i+7 & i\in[1,k+1]\\
2k+i+2 & 4k-i+4 & 8k-2i+6 & i\in[1,k]\\
6k-2i+5 & 9k-i+7 & 9k+i+6 & i\in[1,k]\\
6k-2i+4 & 11k-i+7 & 11k+i+7 & i\in[1,k]\\
/ & 6k+4 & /
\end{array}
\]
$n=12k+11$: 在 $n=12k+7$ 的基础上, 用四元组处理最后四个数.

怎么会有题解只字不提构造思路呢? 真是奇怪.

13.「ARC 160A」Reverse and Count

Link & Submission.

写题解之前, 诚邀您看看一个叫 Rainybunny 的兔子这场比赛的 status. 过题数和 performance 的吐槽在如此励志的比赛历程面前都显得苍白无力. (癫

枚举 $A$ 与 $A_k$ 的 LCP, 字典序小于 $A[:\ell]$ 和字典序不大 $A[:\ell-1](A[\ell]+1)$ 的数量都可以直接算, 那么就能判断当前 LCP 对不对. 注意你甜美的 corner 吧! 精细实现可以 $\mathcal O(n)$.

14.「ARC 160B」Triple Pair

Link & Submission.

\[\textit{ans}=\sum_{t=1}^{\lfloor\sqrt n\rfloor}t^3+\sum_{t=\lfloor\sqrt n\rfloor+1}^n3(n/t)^2.
\]

整除分块 $\mathcal O(T\sqrt n)$.

15.「ARC 160C」Power Up

Link & Submission

设 $f(i,j)$ 表示考虑了原先 $\le i$ 的数, 剩下 $j$ 个 $i$ 的方案数. 每次 $j$ 的上限变化是 $j\gets (j+c_i)/2$, 最终可用的状态数是 $\mathcal O(n)$ 的. 转移可以滚后缀和, 总复杂度 $\mathcal O(n)$.