2019年Angular7——安装搭建路由

Angular 中文官方：https://www.angular.cn/

为什么要看Angular?我也不知道，因为公司有个Angular的项目要维护。听说Angular的版本已经到7了。以前没怎么玩过这个。所以重头开始尝试。还有，我搜了下，最新的angular7搭建的教程很少（是没有）

打开菜鸟教程找Angular的入门教程，不知道为什么只有Angular2，7捏？不过没关系，基础搭建应该都差不多，版本升级可能只是部分语法和接口升级，那就从angular2开始吧。

1.项目搭建

创建与配置项目：http://www.runoob.com/angularjs2/angularjs2-typescript-setup.html

跟着菜鸟教程的“创建配置项目”一步一步来，你也可以

最后一步有点问题，编译并运行应用程序

npm start

报错，报什么错？忘了截图了

报错大概如下：

node_modules/rxjs/Subject.d.ts(16,22): error TS2415:Class'Subject<T>'
  incorrectly extends base class'Observable<T>'.Types of property 'lift' are incompatible.Type'<T, R>(operator: Operator<T, R>) => Observable<T>' is not assignable
  to type '<R>(operator: Operator<T, R>) => Observable<R>'.Type'Observable<T>' is not assignable to type 'Observable<R>'.Type'T' is not assignable to type 'R'.
  npm ERR! code ELIFECYCLE
  npm ERR! errno 2

解决如下：

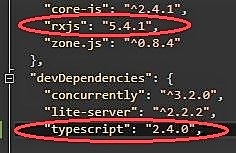
package.json文件里这俩依赖版本的问题

2.写第一个页面

我想写一个列表页、一个详情页、一个编辑页，并且把这三个页面串起来。

等等，我怎么开始写第一个页面呢？菜鸟教程没说啊，angular官网也没说啊

于是我去angular官网找路由的文档：https://www.angular.cn/tutorial/toh-pt5

但是angular官网的代码肯定都是以最新版本为基础的，刚刚跟着菜鸟教程搭的是angular2的环境，直接改版本号升级肯定会有很多问题。所以我想到一个办法，直接把angular官网的路由示例下载下来，这样angular7有了，路由也有了，完美！

angular7路由范例下载（来自官网）： 下载范例

下载解压后，执行 npm install安装

可能会有一些报错，一个一个解决，我遇到的报错有3个：

（1）Failed at the phantomjs-prebuilt@2.1.16 install script.

解决方法，执行：npm install phantomjs-prebuilt@2.1.16 --ignore-scripts

（2）Missing: karma-phantomjs-launcher@^1.0.2

解决方法，执行：npm i karma-phantomjs-launcher

（3）You are running version v8.7.0 of Node.js, which is not supported by Angular CLI v6.

The official Node.js version that is supported is 8.9 and greater.

node版本低的问题

解决方法，windows系统，去nodeJS官网下载最新版本，安装。

最后运行成功

如果它不自动打开浏览，那你手动输入 http://localhost:4200/ （可能你那边不一样）