Project Euler 613 Pythagorean Ant（概率+积分）

题目链接：点击我打开题目链接

题目大意：

给你一只蚂蚁，它在一个 边长为 \(30-40-50\) 的直角三角形\((x,y)\)上，并且它在直角三角形中选择的位置和移动方向的概率都是相等的。问你这只蚂蚁在最长的边上走出去的概率是多少？

注意：以下是题目的解析。

如果你想要享受做数学题的乐趣就不要看下面了啦。(╯￣Д￣)╯╘═╛ (其实看了也无所谓...)

简要题解：

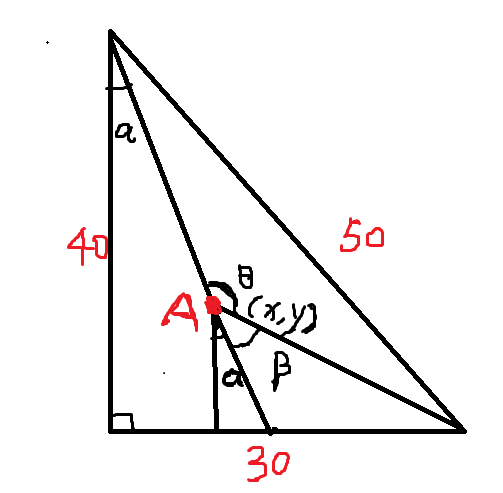
我们假设蚂蚁在 $ A(x,y) $ 点。

枚举一下题意，画一下图...( 随手画的...丑了点...)

我们可以得到：

\(\alpha=\arctan(\frac{x}{40-y})\)

\(\alpha+\beta=\arctan(\frac{30-x}{y})\)

\(\beta=\arctan(\frac{30-x}{y})-\arctan(\frac{x}{40-y})\)

\(\theta=\pi-\left(\arctan(\frac{30-x}{y})-\arctan(\frac{x}{40-y})\right)\)

\(f(x,y)=\frac{\theta}{2\pi}=\frac{1}{2}-\frac{1}{2\pi}*\left(\arctan(\frac{30-x}{y})-\arctan(\frac{x}{40-y})\right)\)

最后积分一下，所以概率就为：

\(ans = \frac{1}{600}*\int_0^{30}\int_0^{40-\frac{40x}{30}}\left[\frac{1}{2}-\frac{1}{2\pi}*\left(\arctan(\frac{30-x}{y})-\arctan(\frac{x}{40-y})\right)\right]\,\mathrm{d}x\mathrm{d}y\)

直接用 \(mma\) ，就很愉快地拿到了\(rank\) \(7\)th啦。