数据结构实现（四）二叉查找树java实现

转载 http://www.cnblogs.com/CherishFX/p/4625382.html

二叉查找树的定义：

　　二叉查找树或者是一颗空树，或者是一颗具有以下特性的非空二叉树：

　　　　1. 若左子树非空，则左子树上所有节点关键字值均小于根节点的关键字；

　　　　2. 若右子树非空，则右子树上所有节点关键字值均大于根节点的关键字；

　　　　3. 左、右子树本身也分别是一颗二叉查找树。

二叉查找树的实现，功能有：

　　1. 用一个数组去构建二叉查找树

　　2. 二叉查找树的中序遍历和层次遍历

　　3. 插入节点

　　4. 查找节点

5. 查找二叉树中的最大值和最小值

　　6.  得到节点的直接父节点

　　7. 得到节点的直接前驱和直接后继节点

　　8. 删除节点

package dataStructures;
 
import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
import java.util.Stack;
 
public class BinarySearchTree {
    private TreeNode<Integer> root = null; // 根节点
 
    public BinarySearchTree() {
    }
 
    // 用一个数组去构建二叉查找树
    public TreeNode<Integer> buildBST(Integer[] array) {
        if (array.length == 0) {
            return null;
        } else {
            root = null; // 初始化树为空树
            for (int i = 0; i < array.length; i++) { // 依次将每个元素插入
                root = insertNode(root, array[i]);
            }
            return root;
        }
    }
 
    // 在二叉查找树中插入一个数据域为data的结点，新插入的结点一定是某个叶子节点
    private TreeNode<Integer> insertNode(TreeNode<Integer> node, Integer data) {
        if (node == null) { // 原树为空，新插入的记录为根节点
            node = new TreeNode<Integer>(data, null, null);
        } else {
            if (node.data != data) { // 树中不存在相同关键字的结点
                if (node.data > data) { // 根节点>插入数据，插入到左子树中
                    node.lchild = insertNode(node.lchild, data);
                } else { // 根节点<插入数据，插入到右子树中
                    node.rchild = insertNode(node.rchild, data);
                }
            }
        }
        return node;
    }
 
    // 二叉查找树的中序遍历，可以得到一个递增的有序数列
    public void inOrder(TreeNode<Integer> node) {
        if (node != null) {
            inOrder(node.lchild);
            System.out.print(node.data + " ");
            inOrder(node.rchild);
        }
    }
 
    // 二叉查找树的层次遍历
    public void levelOrder(TreeNode<Integer> root) {
        Queue<TreeNode<Integer>> nodeQueue = new LinkedList<TreeNode<Integer>>();
        TreeNode<Integer> node = null;
        nodeQueue.add(root); // 将根节点入队
        while (!nodeQueue.isEmpty()) { // 队列不空循环
            node = nodeQueue.peek();
            System.out.print(node.data + " ");
            nodeQueue.poll(); // 队头元素出队
            if (node.lchild != null) { // 左子树不空，则左子树入队列
                nodeQueue.add(node.lchild);
            }
            if (node.rchild != null) { // 右子树不空，则右子树入队列
                nodeQueue.add(node.rchild);
            }
        }
    }
 
    // 查找数据域为data的结点，若不存在，返回null
    public TreeNode<Integer> searchNode(TreeNode<Integer> node, Integer data) {
        while (node != null && node.data != data) {
            if (node.data > data) {
                node = node.lchild; // 根节点>数据，向左走
            } else {
                node = node.rchild; // 根节点<数据，向右走
            }
        }
        return node;
    }
 
    // 查找最大值：不断地寻找右子节点
    public TreeNode<Integer> getMaxData(TreeNode<Integer> node) {
        if (node.rchild == null) {
            return node;
        } else {
            return getMaxData(node.rchild);
        }
    }
 
    // 查找最小值：不断地寻找左子节点
    public TreeNode<Integer> getMinData(TreeNode<Integer> node) {
        if (node.lchild == null) {
            return node;
        } else {
            return getMinData(node.lchild);
        }
    }
 
    // 得到数据域为data的结点的直接父节点parentNode
    public TreeNode<Integer> getParentNode(TreeNode<Integer> root, Integer data) {
        TreeNode<Integer> parentNode = root;
        if (parentNode.data == data) { // 根节点的父节点返回为null
            return null;
        }
        while (parentNode != null) {
            // 查找当前节点的父节点的左右子节点，若是相等，则返回该父节点
            if ((parentNode.lchild != null && parentNode.lchild.data == data)
                    || (parentNode.rchild != null && parentNode.rchild.data == data)) {
                return parentNode;
            } else {
                if (parentNode.data > data) { // 向左查找父节点
                    parentNode = parentNode.lchild;
                } else {
                    parentNode = parentNode.rchild; // 向右查找父节点
                }
            }
        }
        return null;
    }
 
    /**
     * 得到结点node的直接前趋 a.该节点左子树不为空：其前驱节点为其左子树的最大元素
     * b.该节点左子树为空:其前驱节点为其祖先节点(递归)，且该祖先节点的右孩子也为其祖先节点 (就是一直往其parent找，出现左拐后的那个祖先节点)
     */
    public TreeNode<Integer> getPrecessor(TreeNode<Integer> root, TreeNode<Integer> node) {
        if (node == null) {
            return null;
        }
        // a.该节点左子树不为空：其前驱节点为其左子树的最大元素
        if (node.lchild != null) {
            return getMaxData(node.lchild);
        } else { // b.该节点左子树为空: 其前驱节点为其祖先节点(递归)
            TreeNode<Integer> parentNode = getParentNode(root, node.data);
            while (parentNode != null && node == parentNode.lchild) {
                node = parentNode;
                parentNode = getParentNode(root, parentNode.data);
            }
            return parentNode;
        }
    }
 
    /**
     * 得到结点node的直接后继(后继节点就是比要删除的节点的关键值要大的节点集合中的最小值) a.该节点右子树不为空，其后继节点为其右子树的最小元素
     * b.该节点右子树为空，则其后继节点为其祖先节点(递归)，且此祖先节点的左孩子也是该节点的祖先节点，
     * 就是说一直往上找其祖先节点，直到出现右拐后的那个祖先节点：
     */
    public TreeNode<Integer> getSuccessor(TreeNode<Integer> root, TreeNode<Integer> node) {
        if (node == null) {
            return null;
        }
        // a.该节点右子树不为空，其后继节点为其右子树的最小元素
        if (node.rchild != null) {
            return getMinData(node.rchild);
        } else { // b.该节点右子树为空，则其后继节点为其最高祖先节点(递归)
            TreeNode<Integer> parentNode = getParentNode(root, node.data);
            while (parentNode != null && node == parentNode.rchild) {
                node = parentNode;
                parentNode = getParentNode(root, parentNode.data);
            }
            return parentNode;
        }
    }
 
    /**
     * 删除数据域为data的结点 按三种情况处理： a.如果被删除结点z是叶子节点，则直接删除，不会破坏二叉查找树的性质
     * b.如果节点z只有一颗左子树或右子树，则让z的子树成为z父节点的子树，代替z的位置
     * c.若结点z有左、右两颗子树，则令z的直接后继（或直接前驱）替代z，
     * 然后从二叉查找树中删去这个直接后继（或直接前驱）,这样就转换为第一或第二种情况
     *
     * @param node
     *            二叉查找树的根节点
     * @param data
     *            需要删除的结点的数据域
     * @return
     */
    public boolean deleteNode(TreeNode<Integer> node, Integer data) {
        if (node == null) { // 树为空
            throw new RuntimeException("树为空！");
        }
        TreeNode<Integer> delNode = searchNode(node, data); // 搜索需要删除的结点
        TreeNode<Integer> parent = null;
        if (delNode == null) { // 如果树中不存在要删除的关键字
            throw new RuntimeException("树中不存在要删除的关键字！");
        } else {
            parent = getParentNode(node, data); // 得到删除节点的直接父节点
            // a.如果被删除结点z是叶子节点，则直接删除，不会破坏二叉查找树的性质
            if (delNode.lchild == null && delNode.rchild == null) {
                if (delNode == parent.lchild) { // 被删除节点为其父节点的左孩子
                    parent.lchild = null;
                } else { // 被删除节点为其父节点的右孩子
                    parent.rchild = null;
                }
                return true;
            }
            // b1.如果节点z只有一颗左子树，则让z的子树成为z父节点的子树，代替z的位置
            if (delNode.lchild != null && delNode.rchild == null) {
                if (delNode == parent.lchild) { // 被删除节点为其父节点的左孩子
                    parent.lchild = delNode.lchild;
                } else { // 被删除节点为其父节点的右孩子
                    parent.rchild = delNode.lchild;
                }
                delNode.lchild = null; // 设置被删除结点的左孩子为null
                return true;
            }
            // b2.如果节点z只有一颗右子树，则让z的子树成为z父节点的子树，代替z的位置
            if (delNode.lchild == null && delNode.rchild != null) {
                if (delNode == parent.lchild) { // 被删除节点为其父节点的左孩子
                    parent.lchild = delNode.rchild;
                } else { // 被删除节点为其父节点的右孩子
                    parent.rchild = delNode.rchild;
                }
                delNode.rchild = null; // 设置被删除结点的右孩子为null
                return true;
            }
            // c.若结点z有左、右两颗子树，则删除该结点的后继结点，并用该后继结点取代该结点
            if (delNode.lchild != null && delNode.rchild != null) {
                TreeNode<Integer> successorNode = getSuccessor(node, delNode); // 得到被删除结点的后继节点
                deleteNode(node, successorNode.data); // 删除该结点的后继结点
                delNode.data = successorNode.data; // 用该后继结点取代该结点
                return true;
            }
        }
        return false;
 
    }
 
    /**
     * 某些方法的非递归实现 1. 插入节点insertNode(): 2. 二叉查找树的中序遍历： 3. 得到二叉查找树的最大值和最小值：
     */
    // 1. 在二叉查找树中插入一个数据域为data的结点，新插入的结点一定是某个叶子节点
    public TreeNode<Integer> insertNode2(TreeNode<Integer> node, Integer data) {
        TreeNode<Integer> newNode = new TreeNode<Integer>(data, null, null);
        TreeNode<Integer> tmpNode = node; // 遍历节点
        TreeNode<Integer> pnode = null; // 记录当前节点的父节点
 
        if (node == null) { // 原树为空，新插入的记录为根节点
            node = newNode;
            return node;
        }
        while (tmpNode != null) {
            pnode = tmpNode;
            if (tmpNode.data == data) { // 树中存在相同关键字的结点,什么也不做
                return node;
            } else {
                if (tmpNode.data > data) { // 根节点>插入数据，插入到左子树中
                    tmpNode = tmpNode.lchild;
                } else { // 根节点<插入数据，插入到右子树中
                    tmpNode = tmpNode.rchild;
                }
            }
        }
        if (pnode.data > data) {
            pnode.lchild = newNode;
        } else {
            pnode.rchild = newNode;
        }
        return node;
    }
 
    // 2. 二叉查找树的中序遍历LNR，可以得到一个递增的有序数列
    public void inOrder2(TreeNode<Integer> node) {
        Stack<TreeNode<Integer>> nodeStack = new Stack<TreeNode<Integer>>();
        TreeNode<Integer> tempNode = node; // 遍历指针
        while (tempNode != null || !nodeStack.isEmpty()) {
            if (tempNode != null) {
                nodeStack.push(tempNode);
                tempNode = tempNode.lchild;
            } else {
                tempNode = nodeStack.pop();
                System.out.print(tempNode.data + " ");
                tempNode = tempNode.rchild;
            }
        }
    }
 
    // 3.1 查找最大值：不断地寻找右子节点
    public TreeNode<Integer> getMaxData2(TreeNode<Integer> node) {
        TreeNode<Integer> tempNode = node;
        while (tempNode.rchild != null) {
            tempNode = tempNode.rchild;
        }
        return tempNode;
    }
 
    // 3.2 查找最小值：不断地寻找左子节点
    public TreeNode<Integer> getMinData2(TreeNode<Integer> node) {
        TreeNode<Integer> tempNode = node;
        while (tempNode.lchild != null) {
            tempNode = tempNode.lchild;
        }
        return tempNode;
    }
 
    public static void main(String[] args) {
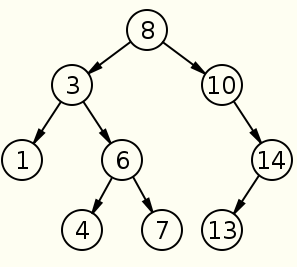
        Integer[] array = { 8, 3, 10, 1, 6, 14, 4, 7, 13 };
        BinarySearchTree bst = new BinarySearchTree();
        TreeNode<Integer> root = bst.buildBST(array);
        System.out.print("层次遍历：");
        bst.levelOrder(root);
 
        System.out.print("\n" + "中序遍历：");
        bst.inOrder(root);
 
        System.out.println();
        System.out.print("得到最大值：");
        System.out.println(bst.getMaxData(root).data);
        System.out.print("得到最小值：");
        System.out.println(bst.getMinData(root).data);
 
        System.out.print("向二叉查找树中插入一个节点，请输入需插入节点的数据域：");
        Scanner input = new Scanner(System.in);
        int data = input.nextInt();
        System.out.print("插入节点" + data + "后，中序遍历的结果：");
        root = bst.insertNode(root, data);
        bst.inOrder(root);
 
        System.out.println("\n" + "在二叉查找树中查找元素," + "请输入需要查找的结点值：");
        data = input.nextInt();
        if (bst.searchNode(root, data) == null) {
            System.out.println("false");
        } else {
            System.out.println("true");
        }
 
        System.out.println("查找节点的直接父节点," + "请输入需要查找的结点值：");
        data = input.nextInt();
        System.out.print("节点" + data + "的父节点是：");
        if (bst.getParentNode(root, data) == null) {
            System.out.println("null");
        } else {
            System.out.println(bst.getParentNode(root, data).data);
        }
 
        System.out.println("删除结点," + "请输入需要删除的结点值：");
        data = input.nextInt();
        if (bst.deleteNode(root, data)) {
            System.out.print("删除结点后的层次遍历：");
            bst.levelOrder(root);
            System.out.print("\n" + "删除结点后的中序遍历：");
            bst.inOrder(root);
        }
 
    }
 
}

逻辑图