《孙子算经》之"物不知数"题：中国剩余定理

1、《孙子算经》之"物不知数"题

今有物不知其数，三三数之剩二，五五数之剩七，七七数之剩二，问物几何？

2、中国剩余定理

定义：

设 a,b,m 都是整数.  如果 m|(a-b),  则称 a 和 b 模 m 同余, 记为

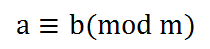
m 称为这个同余式的模.

定理(中国剩余定理):

设 m₁,m₂,...,m_r 是两两互素的正整数. 设 a₁,a₂,...,a_r 是整数, 则同余方程组

模 M = m₁m₂...m_r 有唯一解

3、C语言源代码

 #include<stdio.h>

 //////////////////////////////////////////
 // 作者：落枫飘飘
 // 时间：2016、04、21
 // 博客：http://www.cnblogs.com/wuqianling/p/5415758.html
 //////////////////////////////////////////
 // 《孙子算经》之"物不知数"题：
 // 今有物不知其数，三三数之剩二，五五数之剩七，七七数之剩二，问物几何？
 //////////////////////////////////////////
 // 根据题意我们有如下同余方程组:
 // x=2%3   ---> x=3*k+2
 // x=3%5
 // x=2%7
 //////////////////////////////////////////

 // 分析法求解
 int analytical(float m1, float m2, float m3, float a1, float a2, float a3)
 {
     float x=0.0, k1=0.0, k2=0.0, k3=0.0;

     for(k1 = ; ; k1++)
     {
         x = m1*k1 + a1;       // ---> x=3*k1+2
         k2 = (x-a2) / m2;     // ---> k2=(x-2)/3
         if(k2 == (int)k2)     // 判断k2是否为整数
         {
             k3 = (x-a3) / m3;
             if(k3 == (int)k3) // 判断k3是否为整数
                 break;
         }
     }
     return (int)x;
 }

 // 中国剩余定理求解
 int chineseRemainderTheorem(int m1, int m2, int m3, int a1, int a2, int a3)
 {
     int i, x;
     int M, M1, M2, M3;
     int y1, y2, y3;

     M  = m1 * m2 * m3;
     M1 = m2 * m3;   // M1=M/m1=m2*m3
     M2 = m1 * m3;
     M3 = m1 * m2;
     y1 = M1 % m1;
     y2 = M2 % m2;
     y3 = M3 % m3;
     x  = (a1*M1*y1 + a2*M2*y2 + a3*M3*y3) % M;

     return x;
 }

 int main()
 {
     // x=2%3  即 x=a1%m1
     // x=3%5  即 x=a2%m2
     // x=2%7  即 x=a3%m3
     int m1=, m2=, m3=;
     int a1=, a2=, a3=;
     printf("分析法:\nx=%d \n\n", analytical(m1,m2,m3,a1,a2,a3));
     printf("中国剩余定理:\nx=%d \n\n", chineseRemainderTheorem(m1,m2,m3,a1,a2,a3));
     return ;
 }