高度平衡的二叉搜索树(AVL树)

　　AVL树的基本概念

　　AVL树是一种高度平衡的(height balanced)二叉搜索树：对每一个结点x，x的左子树与右子树的高度差(平衡因子)至多为1。

　　有人也许要问：为什么要有AVL树呢？它有什么作用呢？

　　我们先来看看二叉搜索树吧（因为AVL树本质上是一棵二叉搜索树），假设有这么一种极端的情况：二叉搜索树结点的插入顺序为1,2,3,4,5，也就是：

　　显而易见，这棵二叉搜索树已经其退化成一个链表了，也就是说，它在查找上的优势已经全无了—— 在这种情况下，查找一个结点的时间复杂度是O(n)！

　　如果这棵二叉搜索树是AVL树，在插入顺序仍为1,2,3,4,5的情况下，树的形状如下图：

　　可以看出，AVL树基本操作的最坏时间复杂度要比普通的二叉搜索树低—— 除去可能的插入操作外（我们将假设懒惰删除），它是O(logn)。

　　而插入操作隐含着困难的原因在于，插入一个节点可能破坏AVL树的性质（例如，将6插入到上图的AVL树中会破坏根节点2的平衡条件），如果发生这种情况，就要在插入操作结束之前恢复平衡的性质。事实上，这总可以通过对树进行简单的修正来做到，我们称其为旋转。

　　AVL树的旋转

　　在AVL树中，假设有一个结点的平衡因子为2（最大就是2，因为结点是一个一个地插入到树中的，一旦出现不平衡的状态就会立即进行调整），我们把这个必须重新平衡的结点叫做被破坏点α。这种不平衡只可能是下面四种情况造成的：

　　1. 对α的左儿子的左子树进行了一次插入，即LL情况。
　　2. 对α的左儿子的右子树进行了一次插入，即LR情况。
　　3. 对α的右儿子的左子树进行了一次插入，即RL情况。
　　4. 对α的右儿子的右子树进行了一次插入，即RR情况。

　　情形1和4是关于结点α的镜像对称，2和3也是关于结点α的镜像对称。因此，理论上只有两种情况：第一种情况是插入发生在“外边”的情况（即LL情况或RR情况），第二种情况是插入发生在“内部”的情况（即LR情况或RL情况）。

　　在AVL树中插入结点后，用于保持树的平衡的旋转操作步骤如下：

　　步骤一：沿着插入点到根结点的路径检查结点的平衡因子，找到途中第一个不满足AVL树性质的结点，这个结点就是被破坏点α。

　　步骤二：从被破坏点α开始沿着该路径向下再标记连续的两个结点β、γ，这三个点就是旋转过程将要涉及的三个点（这些点中不一定包括插入点，旋转会使β或γ成为新的根，另外两个点作为根的左右儿子，其他结点根据AVL树的性质放置即可）。

　　步骤三：判断插入点与被破坏点α之间的关系属于上述四种情况中的哪一种：如果是插入发生在“外边”的情况(即LL的情况或RR的情况)，只需要以β为新的根结点顶替被破坏点α的位置进行进行一次单旋转即可完成调整；如果是插入发生在“内部”的情形(即LR的情况或RL的情况)，只需要以γ为新的根结点顶替被破坏点α的位置进行稍微复杂的双旋转即可完成调整。

　　　　　　　　　　　　　　　　　　　　　　　　(1) LL基本情况

　　　　　　　　　　　　　　　　　　　　　　　　(2) RR基本情况

　　　　　　　　　　　　　　　　　　　　　　　　(3) LR基本情况

　　　　　　　　　　　　　　　　　　　　　　　　(4) RL基本情况

　　实例分析

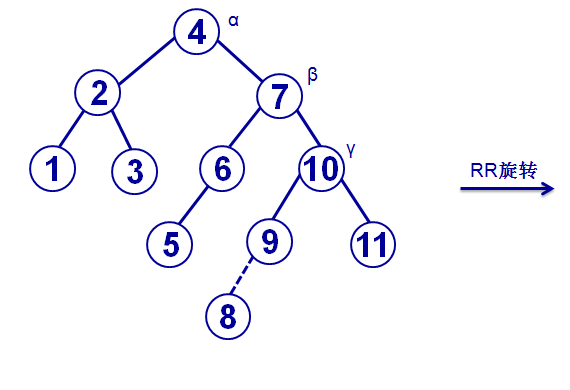
　　下面给出了一个向AVL树中插入关键字的实例，在已给AVL树的基础上插入9（图中虚线表示），沿着插入点9到根节点的路径发现第一个高度不平衡的结点6，即被破坏点；从被破坏点6开始沿着该路径向下标记6,10,7为α,β,γ；插入点9位于被破坏点6的右儿子10的左子树上，所以属于RL状况；以γ结点7为新的根节点顶替被破坏点6的位置，α结点6和β结点10分别为γ结点7的左右儿子，其他结点根据AVL树的性质放置即可得到右侧的AVL树。

　　在上面AVL树的基础上继续插入8（图中虚线表示），沿着插入点8到根节点的路径发现第一个高度不平衡的结点为根节点4，即被破坏点；从被破坏点4开始沿着该路径向下标记4,7,10为α,β,γ；插入点8位于被破坏点4的右儿子7的右子树上，所以属于RR状况；以β结点7为新的根节点顶替被破坏点4的位置，α结点4和γ结点10分别为β结点7的左右儿子，其他结点根据AVL树的性质放置即可得到右侧的AVL树。

　　AVL树是最早的平衡二叉树之一，应用相对其他数据结构较少。Windows对进程地址空间的管理用到了AVL树。

　　参考资料:　　　《算法导论第3版》—— 习题 13-3 AVL树

　　　　　　　　　《数据结构与算法分析—Java语言描述》—— 4.4 AVL树

　　　　　　　　　 http://blog.chinaunix.net/uid-25324849-id-2182877.html