堆的基础题目学习（EPI）

堆的应用范围也比较广泛，经常游走在各种面试题目之前，不论算法设计的题目还是海量数据处理的题目，经常能看到这种数据结构的身影。堆其实就是一个完全二叉树的结构，经常利用数组来实现。包含最大堆和最小堆两种。最大堆的性质：针对每个根节点，其节点值大于其后继节点。最小堆的性质：针对每个根节点，其节点值小于后继节点。

算法设计中堆数据结构一般直接利用STL中实现好的数据结构。其中针对堆数据结构的操作：插入和删除时间复杂度可记为O（lgn），返回最大值/最小值时间复杂度记为O（1）。另外，这里的堆和内存分配中的堆完全没有任何关系，内存分配中的堆一般是一个可用内存空间连接起来的链表，而这个是一种树形的数据结构。

STL堆的使用：

#include <queue>
using namespace std;
//其中priority_queue默认使用的less<T>的比较操作，为最大堆
//如果希望使用最小堆，需要手动配置compare，比如使用greater<T>或者定义一个T类型的比较函数
//返回>为true定义的为最小堆，返回<为true定义的为最大堆
//内置类型的简单声明
priority_queue<int,vector<int>,greater<int> > minqueue;
priority_queue<int,vector<int>,less<int> > maxqueue;
//自定义类型自定义仿函数模板或者重载operator <即可。
#include <iostream>
#include <functional>
#include <queue>
using namespace std;
class person {
public:
	string firstname;
	string secondname;
	person(const string &f,const string &s):firstname(f),secondname(s) {
		;
	}
	friend ostream & operator <<(ostream &os,const person &p1);
};
ostream & operator <<(ostream &os,const person &p1) {
	os<<p1.firstname<<" "<<p1.secondname<<endl;
	return os;
}
template<class T>
class compareMin {
public:
	bool operator()(const T & p1,const T & p2) {
		if(p1.firstname == p2.firstname) {
			return p1.secondname > p2.secondname;
		}
		return p1.firstname > p2.firstname;
	}
};
 
template<class T>
class compareMax {
public:
	bool operator()(const T & p1,const T & p2) {
		if(p1.firstname == p2.firstname) {
			return p1.secondname < p2.secondname;
		}
		return p1.firstname < p2.secondname;
	}
};
int main(void) {
	priority_queue<int,vector<int>,greater<int> > minqueue;
	priority_queue<int,vector<int>,less<int> > maxqueue;
	priority_queue<person,vector<person>,compareMin<person> > minperqueue;
	priority_queue<person,vector<person>,compareMax<person> > maxperqueue;
	minperqueue.push(person("aaa","bbb"));
	minperqueue.push(person("ccc","ddd"));
	minperqueue.push(person("eee","fff"));
	maxperqueue.push(person("aaa","bbb"));
	maxperqueue.push(person("ccc","ddd"));
	maxperqueue.push(person("eee","fff"));
	cout<<minperqueue.top();
	cout<<maxperqueue.top();
}　　

堆的经典应用top k计算，last k计算，中位数的维护；堆的另外的应用场景为多个元素比较操作。

1.在RAM比较受限制的情况下，如何归并k个已经有序的文件。

归并k个有序文件可以利用两两归并的方法，但是这样读写IO比较多，第一次合并的文件读写IO达到了k-1次。效率非常低。

另外一种思路就是k路归并的方法，k路归并的场景是一次需要比较k个数字，也即从k个数字中取出最小，这种使用场景非常吻合最小堆的性质。所以此题目考虑使用最小堆进行k路归并，每次将k个有序文件读取当前文本记录，得到当前最小文本记录，将最小文本记录文件的读取指针后移，这样文件记录IO每个均读写一次，效率比两两归并提高不少。

2.设计一个算法，排序一个k-increasing-decreasing的数组。k-increasing-decreasing数组的定义是，元素大小成波浪状，首先increasing增加然后decreasing，依次交替，且increasing的元素个数+decreasing的个数 = k。举一个例子如下图：

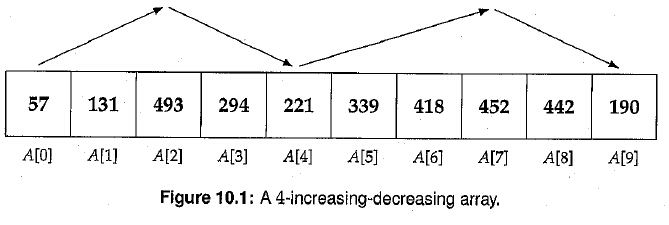
看到这个题目之后由于是英文，把题目的题意理解错了，我以为是要把一个无序的数组排序成k-increasing-decreasing数组，如果题意是这个样子会有很多种答案。

看完答案之后才发现题意没有正确理解。如果为排序k-increasing-decreasing数组，把数组均打断为increasing sorting数组，decreasing的需要逆序一下。因为题目中的增，减区间比较分明，容易处理。然后利用k路归并的方法归并。

3.利用堆的API实现栈和队列的功能。

初遇到这个题目的时候一时也没有思路，后来想回想了一下堆的功能，push，pop，extract-min或者extract-max的功能，所以需要把extract-min或extract-max的功能与先进后出和先进先出的功能对应起来。

后来想到添加元素的时候同时添加一个自增的元素即可，根据自增的元素建立最大堆能够获得栈的接口，根据自增的元素建立最小堆能够获得队列的接口。

4.给定一个点的坐标，然后有一个超大文件为另外一些点的坐标。内存受限的情况下如何找出文件中距离给定坐标距离最近的k个点。

类似top k的算法，创建一个长度为k的最大堆，每次遇到比堆顶距离给定点距离近的点，删除堆顶的点，向堆中压入该坐标点。文件扫描一遍之后及求出了距离最近的k个点。

5.一段整数数据流，找出第k-th大的元素。

利用最小堆，如果当前元素大于根节点元素，则删除根节点元素，加入该元素。最后根节点保存的为第k-th大的元素。

6.给定一个近似有序的数组，每个乱序的元素距离它原位置不超过k个单位，设计一个排序该数组的算法。

利用最小堆，空间设置为O（k），每次拿出最小的元素输出，压入元素。因为乱序元素距离原位置不超过k个单位，所以这样就能够保证输出的最小的均为有序的。

7.设计一个能够在O（n）时间复杂度内返回距离数组中位数元素最近的k个元素。

首先利用快速选择能够在O（n）的时间复杂度内得到中位数。

如果利用堆来实现最近的k个元素为O（nlgk），

另外一种方法，O（n）的时间复杂度内快速选择得到中位数，然后A[i]-中位数得到的新数组中利用快速选择得到第k小的数字，两遍扫描。

然后根据得到的第k小的数字再次扫描即可得到结果。

8.实施计算一个整型数据流的中位数。

利用两个堆来维护中位数，之前的一篇日志详细介绍了一下：求中位数总结。

9.假定一个实数集的表示形式为a+b√2，其中a，b均为大于等于0的整数，求出这个实数集中第k小的元素。比如0+0√2为最小的元素。

这个题目的思路与之前一个面试中挂掉的题目极为的神似。

那个题目是两个有序的数组，A和B，求第k小的A[i]+B[j]。举例来说A[0]+B[0]为最小元素。

还有一个类似的题目为由质因数3,5,7组成的第k小的数字。举例来说3,5,7,9...等等。

其中的思路均是利用最小堆来维护，从堆中获取一个元素之后，向最小堆中加入多个元素比较。需要控制加入顺序或者利用hash表过滤重复。

10.设计一个算法，判断一个最大堆中第k-th大的元素与给定元素x的关系（大于，等于，小于指定元素）。

思路保持两个全局变量，一个记录大于k的元素个数，一个记录等于k的元素的个数，然后递归的计算两个变量。任意一个变量大于k则结束递归即可。

然后根据两个变量来计算第k-th大的元素与给定元素x的关系。