hdu3516 Tree Construction

Problem Description

Consider a two-dimensional space with a set of points (xi, yi) that satisfy xi < xj and yi > yj for all i < j. We want to have them all connected by a directed tree whose edges go toward either right (x positive) or upward (y positive). The figure below shows
an example tree.




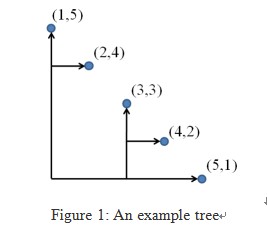
Write a program that finds a tree connecting all given points with the shortest total length of edges.

 

Input

The input begins with a line that contains an integer n (1 <= n <= 1000), the number of points. Then n lines follow. The i-th line contains two integers xi and yi (0 <= xi, yi <= 10000), which give the coordinates of the i-th point.

 

Output

Print the total length of edges in a line.

 

Sample Input

5
1 5
2 4
3 3
4 2
5 1
1
10000 0

 

Sample Output

12
0

这题要注意树的左端点必定在左上端点向下做垂线和右下端点向左作垂线的交点，思路和石子合并差不多，需要用四边形优化。

#include<iostream>
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<queue>
#include<stack>
#include<string>
#include<algorithm>
using namespace std;
#define ll long long
#define inf 999999999
int x[1006],y[1006],dp[1006][1006],s[1006][1006];
int dis(int x1,int y1,int x2,int y2){
    return abs(x1-x2)+abs(y1-y2);
}

int main()
{
    int n,m,i,j,len,k;
    while(scanf("%d",&n)!=EOF)
    {
        for(i=1;i<=n;i++){
            scanf("%d%d",&x[i],&y[i]);
            dp[i][i]=0;
        }
        for(i=1;i<=n-1;i++){
            s[i][i+1]=i;
            dp[i][i+1]=dis(x[i],y[i],x[i+1],y[i+1]);
        }
        for(len=3;len<=n;len++){
            for(i=1;i+len-1<=n;i++){
                j=i+len-1;
                dp[i][j]=inf;

                for(k=s[i][j-1];k<=s[i+1][j];k++){
                    if(dp[i][j]>dp[i][k]+dp[k+1][j]+abs(y[j]-y[k])+abs(x[i]-x[k+1]) ){
                        dp[i][j]=dp[i][k]+dp[k+1][j]+abs(y[j]-y[k])+abs(x[i]-x[k+1]);
                        s[i][j]=k;
                    }
                }
            }
        }
        printf("%d\n",dp[1][n]);

    }
    return 0;
}