MST（最小生成树）

1.prim算法分析

prim算法是用来构建MST(最小生成树)的一种基于贪心策略的算法。prim算法通过维护lowcost数组和closest数组记录每次查询的最小权值边结点。

首先，看一个示例来理解prim算法是怎样构建最小生成树的。我们现在对图a从结点V1开始构建最小生成树，在右边的是当前图的邻接矩阵。

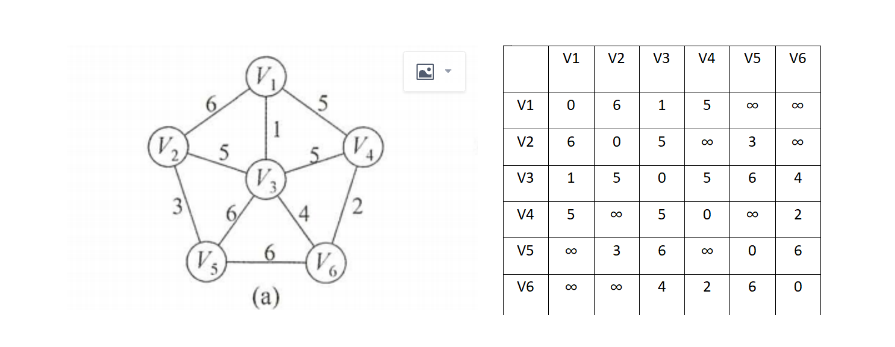
1.先初始化一个lowcost数组和closest数组，并且让lowcost的初始值为v1行的值。让closest数组的值为v1。

2.找到lowcost数组中的最小值（权值为0表示没有边，故非0的最小值），然后记录最小权值和位置，并且加入到最小生成树中。

此时Min = 3，mindex = 3；表示（V1，V3）是本次找到的最小值边，加入MST中，并切将lowcost[mindex]的置为0，表示结点已经加入MST。

3.依据加入的结点V3，更新lowcost数组和closest数组的值。其中Closest中值代表本次查找过程中，权值为lowcost[j]的边是连接MST中哪个结点的。

4.以此循环2~3步骤，直到所有结点加入到MST中。

整个构建过程应该为下图所示：

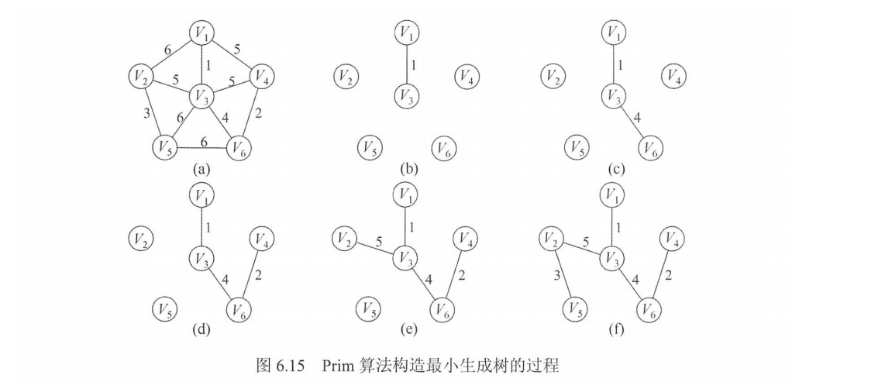
#include<iostream>
#include<cstdio>
#include<cstring>

using namespace std;

#defind MAX 6;
#define MAXCOST 0x7fffffff 

typedef String VertexType;
typedef int EdgeType;
typedef struct {
	VertexType Vex[MAX];
	EdgeType Edge[MAX][MAX];
	int vexnum,arcnum;
}MGragh;

void prim(MGraph G, VertexType v){
	int lowcost[MAX];    //lowcost数组用来更新不在MST中的结点到MST的权值最小的节点；
	int closest[MAX];    //closest数组用来储存是通过哪个结点找到的最小权值边；通过<closest[i],i>找到MST的边；
	int i, j,mindex,min;  //mindex用来记录每次查找的最小权值边的结点； min记录每次查找到的最小权值；
	//初始化 让lowcost[]的值为与v相邻的边的权值。让closest[]的值为v；
	for(int i=0;i<G.vexnum;i++){
		lowcost[i] = G.Edge[v][i];
		closest[i] = v;
	}
	//扫描每个结点
	for(int i=0;i<G.vexnum;i++){
		min = MAXCOST;
		//找到lowcost数组中的最小值，并且记录下来；
		for(int j=0;j<G.vexnum;j++){
			if(lowcost[j] != 0 && lowcost[j] < min ){
				min = lowcost[j];
				mindex = j;
			}
		}
		//把记录的最小权值边和结点加入MST；
		printf("edge(%d,%d) has join the MST,it cost %d",closest[mindex],k,min);
		//更新lowcost和closest数组， 每次加入MST中结点又会产生新的边；所以需要更新lowcost；
		for(int j=0;j<G.vexnum;j++){
			if(G.Edge[mindex][j] !=0  && G.Edge[mindex][j] < lowcost[j]){
				lowcost[j] = G.Edge[mindex][j];
				closest[j] = mindex;
			}
		}
	}

}

2.Kruskal算法分析

kruskal算法也是构建生成树的一种贪心算法，它与prim算法的区别在于：kruskal主要将图中边作为处理对象。它先将图中所有的边信息储存到一个边集合中，然后选择集合中最小权值的边，并且利用vset记录相当边的2个结点是否属同一个集合，若是，则不加入MST中，若不是，则加入MST中。

我们现在对图a利用kurskal算法开始构建最小生成树，在右边的是当前图的邻接矩阵



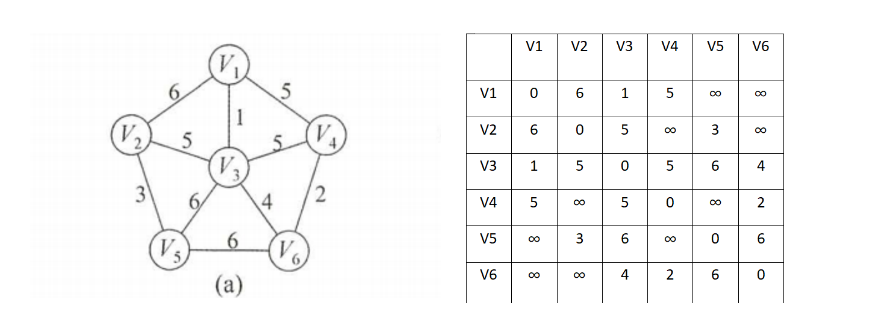
1.初始化一个边集E，和一个辅助数组vset[]用来判断一条边的2个顶点是否属于同一个集合。



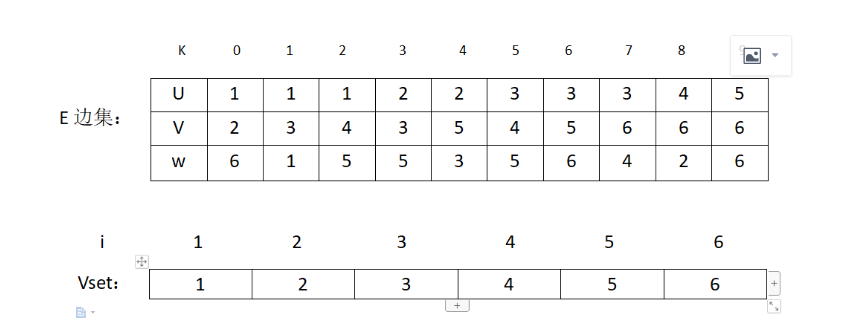
2.然后通过排序算法对边集E排序，选择出最小的权值边。判断选出的边（u，v）是否属于同一集合，判断方法是比较vset[u]和vset[v]的值是否一样。若是一样，则属于同一个集合，不加入MST。若不是则修改所有vset[i] = v的结点让它的值为u ，表示结点u和v所在的集合加入同一集合了。

如：通过堆排序找到了最小权值边（1，3）然后判断vset[1]和vset[3]值是否相同，发现不相同，则加入MST，然后修改vset[3] =vset[1]。执行后表的状态为：



对应的图的状态为：



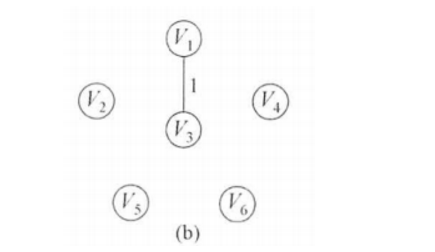
接下来是边（4，6），它的权值为2。判断发现结点v4，v6不是同一集合，加入MST。修改表格



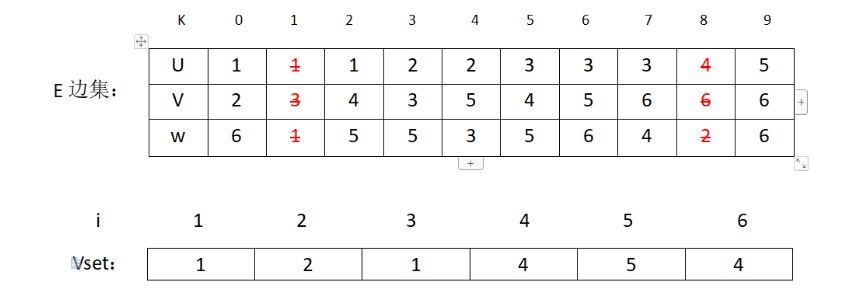
对应图的状态为：



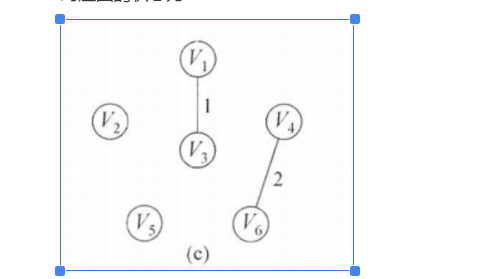
接下来是（2，5）权值为3，然后加入MST，修改表格



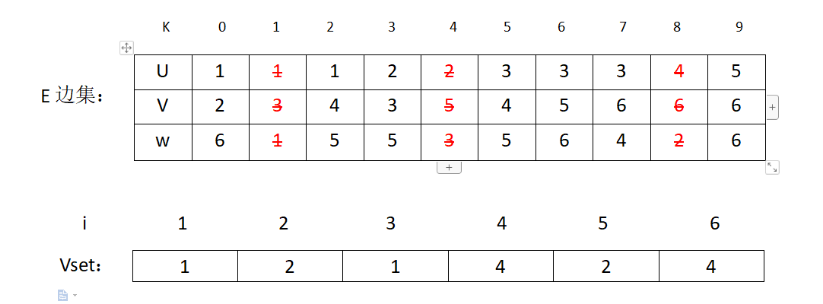
对应图的状态：



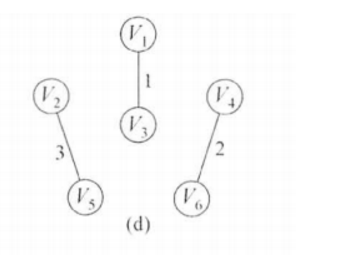
接下来是边（3，6），V3和V6也不是同一集合，加入MST。修改表格：



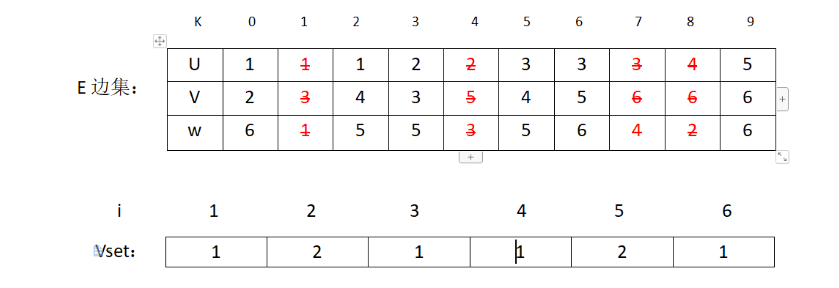
对应图的状态：



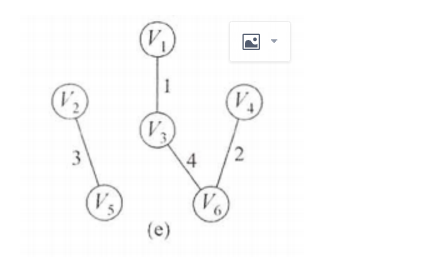
接下来是边（1，4）v1和v4属于同一集合，则不加入MST。表格为：



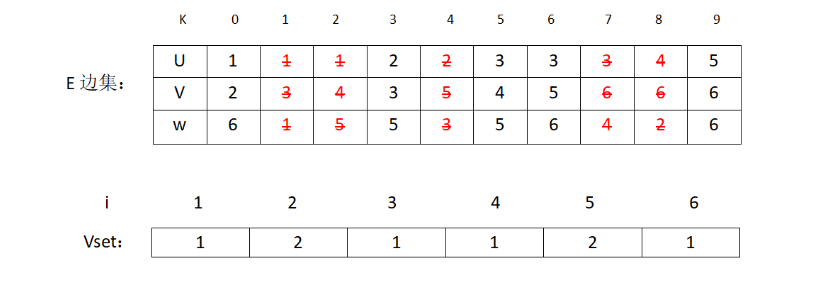
接下来是（2，3） v2和v3不在同一个集合，加入MST，修改表格：



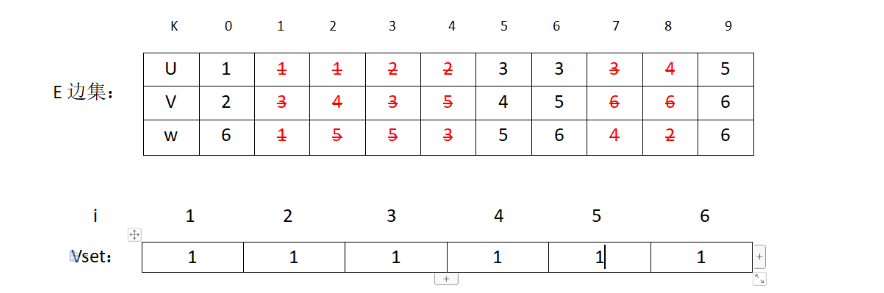
对应图状态为：



到此，所有的结点都在同一集合，MST构建完毕。

 typedef struct{
    char vertex[VertexNum];                //顶点表
    int edges[VertexNum][VertexNum];       //邻接矩阵,可看做边表
    int n,e;                               //图中当前的顶点数和边数
}MGraph; 

typedef struct node {
    int u;                                //边的起始顶点
    int v;                                //边的终止顶点
    int w;                                //边的权值
}Edge; 

void kruskal(MGraph G){
    int i,j,u1,v1,sn1,sn2,k;
    int vset[VertexNum];                  //辅助数组。判定两个顶点是否连通
    Edge E[EdgeNum];                       //存放全部的边
    k=0;                          //E数组的下标从0開始
    //
    for (i=0;i<G.n;i++){
        for (j=0;j<G.n;j++){
            if (G.edges[i][j]!=0 && G.edges[i][j]!=INF){
                E[k].u=i;
                E[k].v=j;
                E[k].w=G.edges[i][j];
                k++;
            }
        }
    }
    heapsort(E,k,sizeof(E[0]));            //堆排序，按权值从小到大排列
    for (i=0;i<G.n;i++) {                   //初始化辅助数
        vset[i]=i;
    }
    k=1;                                  //生成的边数，最后要刚好为总边数
    j=0;                                  //E中的下标
    while (k<G.n){
        sn1=vset[E[j].u];
        sn2=vset[E[j].v];                //得到两顶点属于的集合编号
        if (sn1!=sn2){           //不在同一集合编号内的话，把边增加最小生成树
            printf("%d ---> %d, %d",E[j].u,E[j].v,E[j].w);
            k++;
            for (i=0;i<G.n;i++){
                if (vset[i]==sn2){
                    vset[i]=sn1;
                }
            }
        }
        j++;
    }
}