P4568 [JLOI2011]飞行路线 / P2939 [USACO09FEB]Revamping Trails G

题目描述

Link

Alice 和 Bob 现在要乘飞机旅行，他们选择了一家相对便宜的航空公司。该航空公司一共在 \(n\) 个城市设有业务，设这些城市分别标记为 \(0\) 到 \(n-1\)，一共有 \(m\) 种航线，每种航线连接两个城市，并且航线有一定的价格。

Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市，途中可以进行转机。航空公司对他们这次旅行也推出优惠，他们可以免费在最多 \(k\) 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少？

分层图最短路的模板题。

发现自己好久不打，都快忘了怎么写了，临近 Csp，赶快复习一下。

分层图就是每一层都是一张原图，层与层之间在由边连接起来的图。

分层图具体表示的是使用 \(j\) 次免费通行的权限后到达 \(u\) 点的状态。

关于这道题，我们考虑怎么建图。

使用一张飞机票就代表我们走这条边的代价为 \(0\) ,我们可以有 \(i\) 这一层到 \(i+1\) 这一层的 \(u-v\) 连一条边权为零的边，

表示我们从 \(u\) 这个点到 \(v\) 这个点不需要花费代价。

为什么要往每一层都连边，是因为你坐飞机的顺序是不确定的。

图建出来大概长这样：

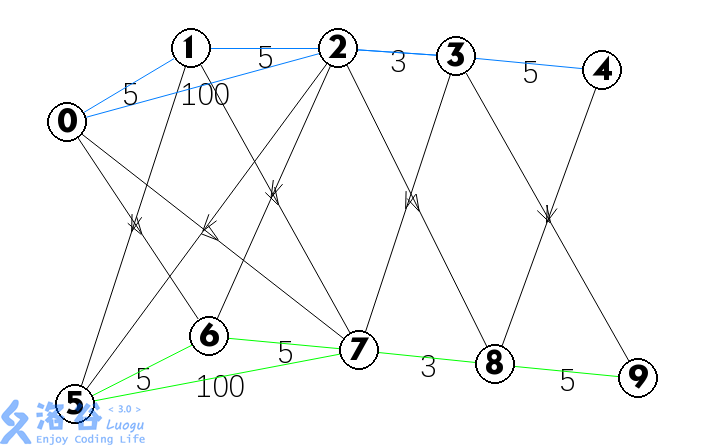
还要注意的点就是每一层的终点之间也要互相连边，因为你免费次数用几次可能会比都用完的方案要优。

我们最后最短路经过的边权为 \(0\) 的条数就是我们要用的免费次数。

关于 \(spfa\) ,他死了。别问我是怎么知道的，我就是在这里被卡的。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<cstring>
using namespace std;
const int N = 1e6+10;
struct node{int to,net,w;}e[2500010];
priority_queue< pair<int , int> , vector< pair<int,int> > , greater< pair<int,int> > >q;
int n,m,k,x,y,w,tot,s,t;
int dis[N],head[N];
bool vis[N];
inline int read()
{
	int s = 0, w = 1; char ch = getchar();
	while(ch < '0' || ch > '9') {if(ch == '-') w = -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){s = s * 10 + ch -'0';ch = getchar();}
	return s * w;
}
void add(int x , int y , int w)
{
	e[++tot].to = y;
	e[tot].w = w;
	e[tot].net = head[x];
	head[x] = tot;
}
void dfs(int x)//dij
{
	memset(dis , 0x3f3f3f , sizeof(dis));
	q.push(make_pair(0,x));
	dis[x] = 0;
    while(!q.empty())
    {
    	int t = q.top().second;  q.pop();
    	if(vis[t]) continue;
		vis[t]  = 1;
		for(int i = head[t]; i; i = e[i].net)
		{
			int to = e[i].to;
			if(dis[to] > dis[t] + e[i].w)
			{
				dis[to] = dis[t] + e[i].w;
				q.push(make_pair(dis[to] , to));
			}
		}
    }
}
int main()
{
	n = read(); m = read(); k = read();
	s = read(); t = read();
	for(int i = 1; i <= m; i++)
	{
		x = read(); y = read(); w = read();
		add(x,y,w); add(y,x,w);//原图上连边
		for(int i = 1; i <= k; i++)
		{
			add(x + n * (i-1) , y + n * i , 0);//层与层之间的点连一条边权为0的边
			add(y + n * (i-1) , x + n * i , 0);
			add(x + n * i , y + n * i , w);//每一层按原图连边
			add(y + n * i , x + n * i , w);
		}
	}
	for(int i = 1; i <= k; i++) add(t + n * (i-1) , t + n * i , 0);//每一层终点之间互相连边
	dfs(s);
	printf("%d\n",dis[t + n * k]);
	return 0;
}