tyvj 1198 矩阵连乘——区间dp

tyvj 1198 矩阵连乘

题目描述

一个n*m矩阵由n行m列共n*m个数排列而成。两个矩阵A和B可以相乘当且仅当A的列数等于B的行数。一个N*M的矩阵乘以一个M*P的矩阵等于一个N*P的矩阵，运算量为n*m*p。 矩阵乘法满足结合律，A*B*C可以表示成(A*B)*C或者是A*(B*C)，两者的运算量却不同。例如当A=2*3 B=3*4 C=4*5时，(A*B)\*C=64而A\*(B*C)=90。显然第一种顺序节省运算量。 现在给出N个矩阵，并输入N+1个数，第i个矩阵是a[i-1]*a[i]。

输入格式

第一行n(n<=100)；

第二行n+1个数；

输出格式

最优的运算量

样例

样例输入

 3
 2 3 4 5

样例输出

 64

解释：

可能大部分同学连题目都没有看懂，其实是很好理解的。

如题目中的A、B、C，A*B=2*3*4，B*C=3*4*5。

可以这么理解：两个矩阵（长宽中必须有一个相同）相乘，讲相同部分放中间，剩下两个不同的部分在两边相乘。如：A：x*y

B：y*z

C：z*l

A*B=x*y*z; B*C=y*z*l;

那么三个矩阵相乘是什么样的呢？

还是按上面的例子：(A*B)*C=(x*y*z)*C，显然A*B后的矩阵长宽都发生了变化，变化的是：y的边去掉，x与z取相乘，则乘了后，矩阵变为了x*z

如图：

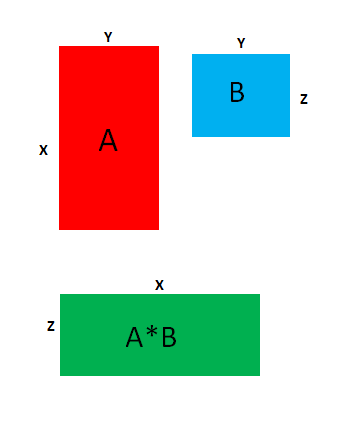
所以，则(A*B)*C=(x*y*z)+(x*z*l)，A*(B*C)=(x*y*l)+(y*z*l)

注意：

题中求的是运算量，与矩阵相乘后的结果不一样，相乘后的结果只是用来求下一次相乘的运算量。

样例模拟：

a[i]与a[i+1]即第i个矩阵

A：2*3；B：3*4；C：4*5

(A*B)*C：2*3*4+2*4*5=64；

A*(B*C)：2*3*5+3*4*5=90；

故最小的运算量=64

动态转移方程：

 f[i][j]=min(f[i][j],f[i][k]+f[k+1][j]+a[i-1]*a[j]*a[k]);

f[i][j]：从i到j的最小的运算量

f[i][j]之间分开，分成i到k与k+1到j两个区间，现在就可以看出是很简单区间dp，在将运算量加上，取最小值

代码：

#include<bits/stdc++.h>
using namespace std;
const int maxe=1e2+,maxn=1e2+,INF=0x3f3f3f3f;
int n,m,f[maxe][maxe],sum[maxn],a[maxn];
int main(){
    cin>>n;
    memset(f,0x3f,sizeof(f));//初始成最大去最小值
    for(int i=;i<=n;i++)cin>>a[i];
    for(int i=;i<=n+;i++)f[i][i]=;//相同之间的运算量为0
    for(int d=;d<=n;d++){//枚举长度
        for(int i=,j;(j=i+d-)<=n;i++){
            for(int k=i;k<j;k++){
                f[i][j]=min(f[i][j],f[i][k]+f[k+][j]+a[i-]*a[j]*a[k]);
            }
        }
    }
    cout<<f[][n]<<endl;//输出1到n的最小运算量
　　 return 0;
}