最长回文子串的Manacher算法

对于一个比较长的字符串，O(n^2)的时间复杂度是难以接受的。Can we do better?

先来看看解法2存在的缺陷。

1) 由于回文串长度的奇偶性造成了不同性质的对称轴位置，解法2要对两种情况分别处理；
2) 很多子串被重复多次访问，造成较差的时间效率。

缺陷2）可以通过这个直观的小体现：

char: a b a b a

  i : 0 1 2 3 4

当i==1，和i==2时，左边的子串aba分别被遍历了一次。

如果我们能改善解法2的不足，就很有希望能提高算法的效率。Manacher正是针对这些问题改进算法。

(1) 解决长度奇偶性带来的对称轴位置问题

Manacher算法首先对字符串做一个预处理，在所有的空隙位置(包括首尾)插入同样的符号，要求这个符号是不会在原串中出现的。这样会使得所有的串都是奇数长度的。以插入#号为例：

aba  ———>  #a#b#a#

abba ———>  #a#b#b#a#

插入的是同样的符号，且符号不存在于原串，因此子串的回文性不受影响，原来是回文的串，插完之后还是回文的，原来不是回文的，依然不会是回文。

(2) 解决重复访问的问题

我们把一个回文串中最左或最右位置的字符与其对称轴的距离称为回文半径。Manacher定义了一个回文半径数组RL，用RL[i]表示以第i个字符为对称轴的回文串的回文半径。我们一般对字符串从左往右处理，因此这里定义RL[i]为第i个字符为对称轴的回文串的最右一个字符与字符i的距离。对于上面插入分隔符之后的两个串，可以得到RL数组：

char:    # a # b # a #

 RL :    1 2 1 4 1 2 1

RL-1:    0 1 0 3 0 1 0

  i :    0 1 2 3 4 5 6

char:    # a # b # b # a #

 RL :    1 2 1 2 5 2 1 2 1

RL-1:    0 1 0 1 4 1 0 1 0

  i :    0 1 2 3 4 5 6 7 8

上面我们还求了一下RL[i]-1。通过观察可以发现，RL[i]-1的值，正是在原本那个没有插入过分隔符的串中，以位置i为对称轴的最长回文串的长度。那么只要我们求出了RL数组，就能得到最长回文子串的长度。

于是问题变成了，怎样高效地求的RL数组。基本思路是利用回文串的对称性，扩展回文串。

我们再引入一个辅助变量MaxRight，表示当前访问到的所有回文子串，所能触及的最右一个字符的位置。另外还要记录下MaxRight对应的回文串的对称轴所在的位置，记为pos，它们的位置关系如下。

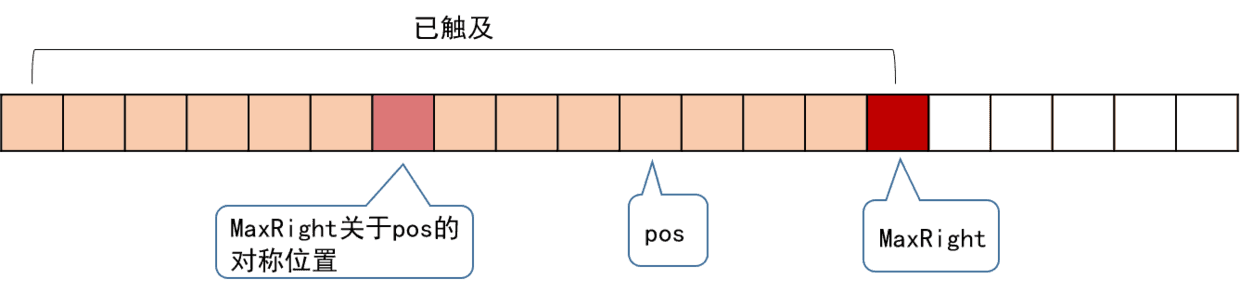
我们从左往右地访问字符串来求RL，假设当前访问到的位置为i，即要求RL[i]，在对应上图，i必然是在po右边的(obviously)。但我们更关注的是，i是在MaxRight的左边还是右边。我们分情况来讨论。

1）当`i`在`MaxRight`的左边

情况1)可以用下图来刻画：

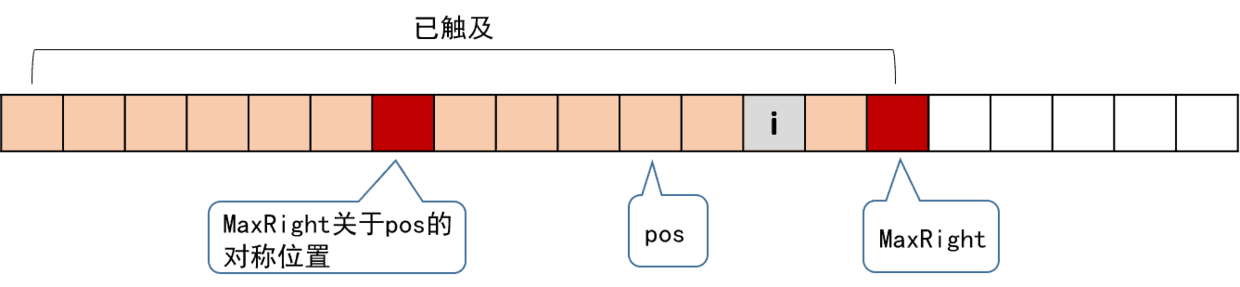
我们知道，图中两个红色块之间（包括红色块）的串是回文的；并且以i为对称轴的回文串，是与红色块间的回文串有所重叠的。我们找到i关于pos的对称位置j，这个j对应的RL[j]我们是已经算过的。根据回文串的对称性，以i为对称轴的回文串和以j为对称轴的回文串，有一部分是相同的。这里又有两种细分的情况。

以j为对称轴的回文串比较短，短到像下图这样。

这时我们知道RL[i]至少不会小于RL[j]，并且已经知道了部分的以i为中心的回文串，于是可以令RL[i]=RL[j]。但是以i为对称轴的回文串可能实际上更长，因此我们试着以i为对称轴，继续往左右两边扩展，直到左右两边字符不同，或者到达边界。

以j为对称轴的回文串很长，这么长：

这时，我们只能确定，两条蓝线之间的部分（即不超过MaxRight的部分）是回文的，于是从这个长度开始，尝试以i为中心向左右两边扩展，，直到左右两边字符不同，或者到达边界。

不论以上哪种情况，之后都要尝试更新MaxRight和pos，因为有可能得到更大的MaxRight。

具体操作如下：

step 1: 令RL[i]=min(RL[2*pos-i], MaxRight-i)

step 2: 以i为中心扩展回文串，直到左右两边字符不同，或者到达边界。

step 3: 更新MaxRight和pos

2）当`i`在`MaxRight`的右边

遇到这种情况，说明以i为对称轴的回文串还没有任何一个部分被访问过，于是只能从i的左右两边开始尝试扩展了，当左右两边字符不同，或者到达字符串边界时停止。然后更新MaxRight和pos。

 1 //最长回文子串的Manacher算法

 2 #include<iostream>

 3 #include<string>

 4 #include<vector>

 5 #include<algorithm>

 6 using namespace std;

 7 void Manacher(string& s,vector<int>& p)

 8 {

 9     int id = 0;

10     int mx = 0;

11     for (int i = 1; i < s.size(); i++)

12     {

13         //i在边界的左边

14         if (mx > i)

15         {

16             p[i] = min(p[2*id-i],mx-i);//p[i]与mx-i的大小关系

17         }

18         else//i在边界的右边

19         {

20             p[i] = 1;

21         }

22         while (s[i+p[i]] == s[i-p[i]])

23             p[i]++;

24         if (i + p[i] > mx)

25         {

26             mx = i + p[i];

27             id = i;

28         }

29     }

30 }

31 int main()

32 {

33     string str;

34     cin >> str;

35     string s = "$";

36     for (unsigned i = 0; i < str.size(); i++)

37     {

38         s += "#";

39         s += str[i];

40     }

41     s += "#";

42     int n = s.size();

43     vector<int> p(n,0);

44     Manacher(s,p);

45     cout<<*max_element(p.begin(),p.end())-1;

46     return 0;

47 }