拦截导弹简单版——线性dp

题目描述

某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度（雷达给出的高度数据是不大于30000的正整数，导弹数不超过1000），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

样例

样例输入

389 207 155 300 299 170 158 65

样例输出

6
2

分析：本题共两问：第一问可以等价为求最大不上升子序列。这样问题就简单了。

首先定义一个i和j。j想对于i更新较快，j<=i。

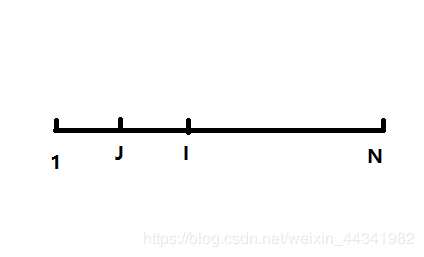
定义f[i]表示从1到i的最大非上升子序列长度,a[i]为i的高度。如果a[j]>a[i]那么f[i]就可能需要更新所以f[i]=max(f[i],f[j]+1);

1 for(int i=1;i<=n;i++){
2 f[i]=1; //一定不要忘记第一个也算一个
3 for(int j=1;j<i;j++){
4 if(h[i]<=h[j]) f[i]=max(f[i],f[j]+1);
5 }
6 maxx=max(maxx,f[i]);
7 } 

核心代码

第二问我一开始想的是用多次求最长不上升子序列，但这个想法显然是错的比如“7 5 4 1 6 3 2”用多次求最长不上升序列所有为”7 5 4 3 2”,
”1”,”6”共3套系统;但其实只要2套,分别为:”7 5 4 1”与”6 3 2”。

正确做法（还有一种做法，效率（n2），超时了，就不说了）第二问的,我们需要用到Dilworth定理:最少链划分=最长反链长度

for(int i=1;i<=n;i++){
g[i]=1;
for(int j=1;j<i;j++){
if(h[i]>h[j]) //求最长上升子序列的长度
g[i]=max(g[i],g[j]+1);
}
mixn=max(mixn,g[i]);
}

核心代码

#include<bits/stdc++.h>
using namespace std;
const int L=200+100;
int n=1,h[L],a[L],f[L],g[L],maxx=-11111111,mixn=-11111111;
int main(){
    while (scanf("%d",&h[n])!=EOF)
        n++;
    n--;
    for(int i=1;i<=n;i++){
    f[i]=1; //记录第i个前面的最长不上升子序列的长度
    for(int j=1;j<i;j++){
        if(h[i]<=h[j]) f[i]=max(f[i],f[j]+1);
    }
    maxx=max(maxx,f[i]);
    }
    for(int i=1;i<=n;i++){
    g[i]=1;
    for(int j=1;j<i;j++){
    if(h[i]>h[j]) //求最长上升子序列的长度
        g[i]=max(g[i],g[j]+1);
    }
    mixn=max(mixn,g[i]);
    }
    printf("%d\n%d\n",maxx,mixn);
    return 0;
}

完整代码