POJ - 3162 Walking Race 树形dp 单调队列

POJ - 3162Walking Race

　　题目大意：有n个训练点，第i天就选择第i个训练点为起点跑到最远距离的点，然后连续的几天里如果最远距离的最大值和最小值的差距不超过m就可以作为观测区间，问这样的区间最长的长度？

　　一开始楞是没看懂题意，最讨厌这种四级题，这是在刁难我英语小能手（能用翻译的就不自己动手）。而且这题感觉单调队列那里的处理更难一点，不过还是来说一说怎么树形dp取得最远距离，先画个简简单单丑丑的图

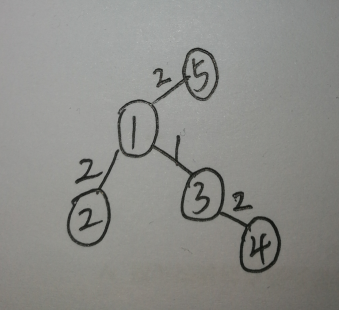
　　我们直接从1作为根节点开始dfs的话,可以处理1的最远距离，并且可以得出到其它节点在其子树中的最短距离，然后怎么得到其他节点的最远距离呢？我们还是从1开始，2的最短距离无非就是1和2连接这一条边再加上除这条外的最长分支也就是1和4这条边，而3的话1和3连接的这条边是在1和4这条路径上的，所以对3来说最远距离就是1的除1和4这条外其他最长分支加上1和3连接的这条边与3和4连接的这条边中的最大值，所以我们可以更新一个每个节点的最大距离以及第二远距离还有最远距离来自哪个子节点的方向。

　　这样的话先一遍dfs得出作为根节点的情况，还有其他节点到子树的情况，然后第二边dfs再由根节点去传入数据更新其他节点的最大值，也就判断子节点是否是最远距离方向的，是的话传入第二远距离，否则传入最远距离。

　　然后就是取区间那里了，首先尺取思想，但需要一个单调递减队列维护区间最大值（最大值在队列首部），然后还需要一个单调递增队列维护区间最小值（最小值在队列首部），然后区间往右的同时，更新左端，详情见代码。

 #include<cstdio>
 #include<queue>
 #include<algorithm>
 using namespace std;
 const int N=;
 struct Side{
     int v,ne,len;
 }S[*N];
 int sn,n,m,head[N],dis1[N],dis2[N],path[N];
 void add(int u,int v,int c)
 {
     S[sn].v=v;
     S[sn].len=c;
     S[sn].ne=head[u];
     head[u]=sn++;
 }
 void updata(int u,int v,int dis)//更新距离
 {
     if(dis>dis1[u])//更新最大距离的来源点
         path[u]=v;
     dis2[u]=max(dis2[u],min(dis1[u],dis));
     dis1[u]=max(dis1[u],dis);
 }
 void dfs1(int u,int f)
 {
     for(int i=head[u];i!=-;i=S[i].ne)
     {
         int v=S[i].v;
         if(v!=f)
         {
             dfs1(v,u);//先搜索子节点
             updata(u,v,dis1[v]+S[i].len);//更新
         }
     }
 }
 void dfs2(int u,int f,int len)
 {
     updata(u,f,len);//由父节点传入的距离更新距离
     for(int i=head[u];i!=-;i=S[i].ne)
     {
         int v=S[i].v;
         if(v!=f)
         {
             if(v==path[u])
                 dfs2(v,u,dis2[u]+S[i].len);
             else
                 dfs2(v,u,dis1[u]+S[i].len);
         }
     }
 }
 int main()
 {
     int f,d;
     while(~scanf("%d%d",&n,&m))
     {
         for(int i=;i<=n;i++)
         {
             head[i]=-;
             dis1[i]=dis2[i]=;
         }
         sn=;
         for(int i=;i<n;i++)
         {
             scanf("%d%d",&f,&d);
             add(i+,f,d);
             add(f,i+,d);
         }
         dfs1(,);
         dfs2(,,);
         deque<int> qx,qd;//qx单调递增队列，qd单调递减队列
         int ans=;         //注意是双向队列，单向没有back()
         for(int i=,j=;i<=n;i++)//j是左端，i是右端
         {
             //维护单调性
             while(qd.size()&&dis1[qd.back()]<dis1[i])
                 qd.pop_back();
             while(qx.size()&&dis1[qx.back()]>dis1[i])
                 qx.pop_back();
             qd.push_back(i);
             qx.push_back(i);
             while(qd.size()&&qx.size()&&dis1[qd.front()]-dis1[qx.front()]>m)
             {
                 //当最大值减最小值大于m时这时左端的位置就需要调整了
                 //左端肯定是要调整到最大值和最小值中较近的位置的前面
                 if(qd.front()<qx.front())
                 {
                     j=qd.front();
                     qd.pop_front();
                 }
                 else
                 {
                     j=qx.front();
                     qx.pop_front();
                 }
                 //把区间外的数全部弹出
                 while(qd.size()&&qd.front()<=j)
                     qd.pop_front();
                 while(qx.size()&&qd.front()<=j)
                     qx.pop_front();
             }
             ans=max(ans,i-j);//更新区间长度
         }
         printf("%d\n",ans);
     }
     return ;
 }

简简单单的低调

　　连做了几题树形dp，不怎么说得出，不过感觉还是有点心得的。核心的思想还是在于它的一棵数的结构，我们可以把某个节点假设为根节点再由它的情况去推导出整棵树的情况。而且精华部分也正如dp，搞清楚dp什么，然后是状态转移的过程。想练好它，无疑就两个方法，做题，思考。