GA函数优化

一、遗传算法简介

        遗传算法（Genetic Algorithms，GA）是1962年美国人提出，模拟自然界遗传和生物进化论而成的一种并行随机搜索最优化方法。 与自然界中“优胜略汰，适者生存”的生物进化原理相似，遗传算法就是在引入优化参数形成的编码串联群体中，按照所选择的适应度函数并通过遗传中的选择、交叉和变异对个体进行筛选，使适应度值号的个体被保留，适应度差的个体被淘汰，新的群体既继承了上一代的信息，又优于上一代。这样反复循环，直至满足条件。

 

二、遗传算法的基本要素

遗传算法的基本要素包括染色体编码方法、适应度函数、遗传操作和运行参数。
其中染色体编码方法是指个体编码方法，目前包括二进制法、实数法等。二进制法是指把个体编码成为一个二进制串，实数法是指把个体编码成为一个实数串。
适应度函数是指根据进化目标编写的计算个体适应度值的函数，通过适应度函数计算每个个体的适应度值，提供给选择算子进行选择。
遗传操作是指选择、交叉和变异操作。
运行参数是遗传算法在初始化时确定的参数，主要包括群体大小M、遗传代数G、交叉概率Pc和变异概率Pm。

 

三、遗传算法的基本操作

选择操作是指从旧群体中以一定概率选择个体到新群体中，个体被选中的概率跟适应度值有关，个体适应度值越好，被选中的概率越大。
交叉操作是指从个体中选择两个个体，通过两个染色体的交换组合，来产生新的优秀个体。交叉过程为从群体中任选两个染色体，随机选择一点或多点染色体位置进行交换。
交叉操作如下图1所示。

 

 

变异操作是指从群体中任选一个个体，选择染色体中的一点进行变异以产生更优秀的个体。
变异操作如下图2所示。

 

 

 

四、遗传算法基本流程

        遗传算法的基本流程可以用下图表示：

GA基本运算过程：
a)初始化：设置进化代数计数器t=0，设置最大进化代数T，随机生成M个个体作为初始群体P(0)。
b)个体评价：计算群体P(t)中各个个体的适应度。
c)选择运算:将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。
d)交叉运算：将交叉算子作用于群体。遗传算法中起核心作用的就是交叉算子。
e)变异运算：将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。
f)终止条件判断:若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出，终止计算。

五、函数分析

1.Griewank()

1.1计算公式

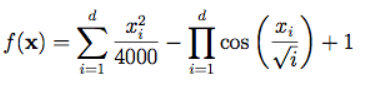
1.2函数图像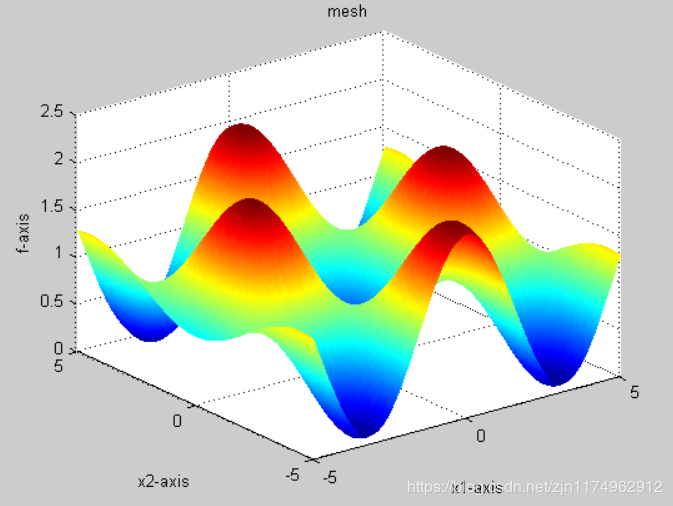 1.3

1.3代码

function y = Griewank(x)
%Griewan函数
%输入x，给出相应的y值，在x=(0,0,…,0)处有全局极小点0
[row,col] = size(x);
if row > 1
error('输入的参数错误');
end
y1 = 1/4000*sum(x.^2);
y2 = 1;
for h = 1:col
y2 = y2*cos(x(h)/sqrt(h));
end
y = y1-y2+1;
%y = -y;
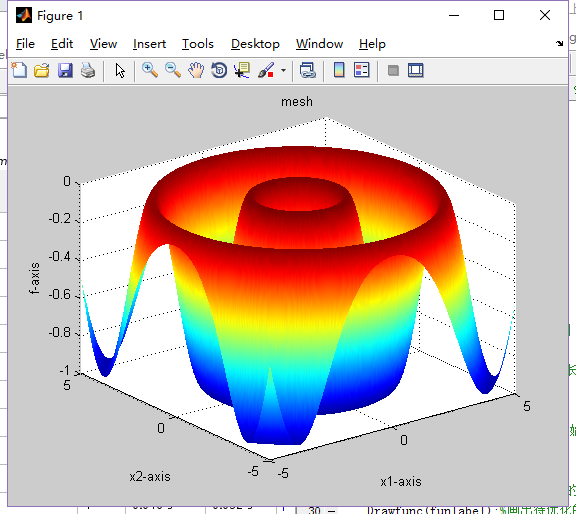
2.Schaffer()

2.1函数公式

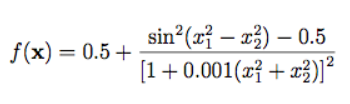
2.2函数图像

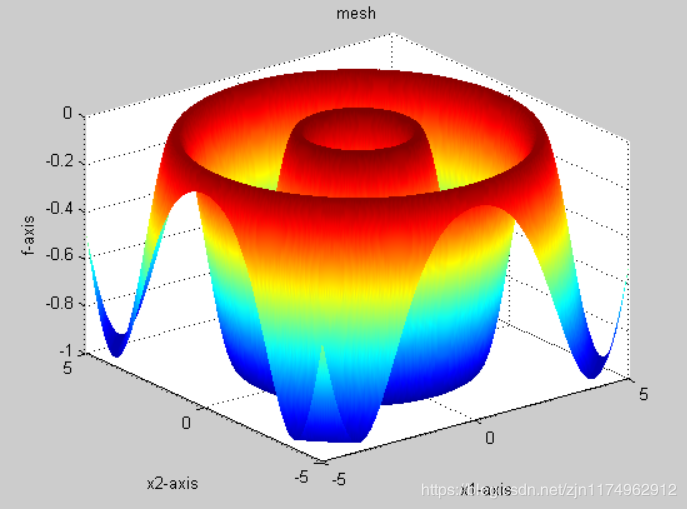
2.3代码

function y = Schaffer(x)
%Schaffer函数
%输入x，给出相应的y值，在x=(0,0,…,0)处有全局极大点1
[row,col] = size(x);
if row > 1
error('输入的参数错误');
end
y1 = x(1,1);
y2 = x(1,2);
temp = y1^2 + y2^2;
y = 0.5 - (sin(sqrt(temp))^2-0.5)/(1+0.001*temp)^2;
y = -y;
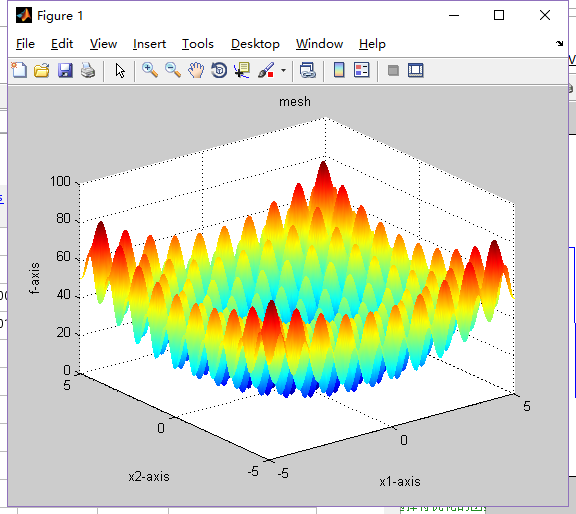
3.Rastrigrin()

3.1函数公式

3.2函数图像

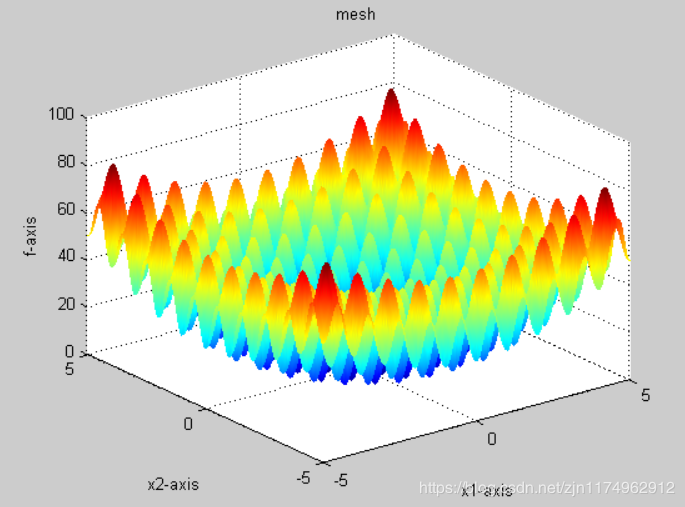
3.3代码

function y = Rastrigrin(x)
% Rastrigrin函数
% 输入x，给出相应的y值，在x = ( 0 , 0 ,…, 0 )处有全局极小点0
[row,col] = size(x);
if row > 1
error( ' 输入的参数错误 ' );
end
y = sum(x.^2-10*cos(2*pi*x)+10);
%y = -y;
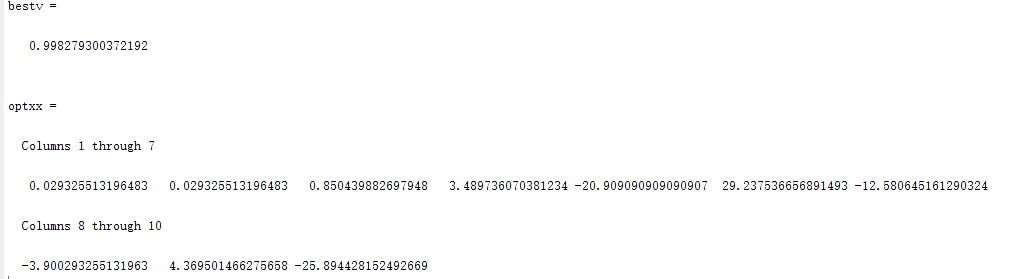
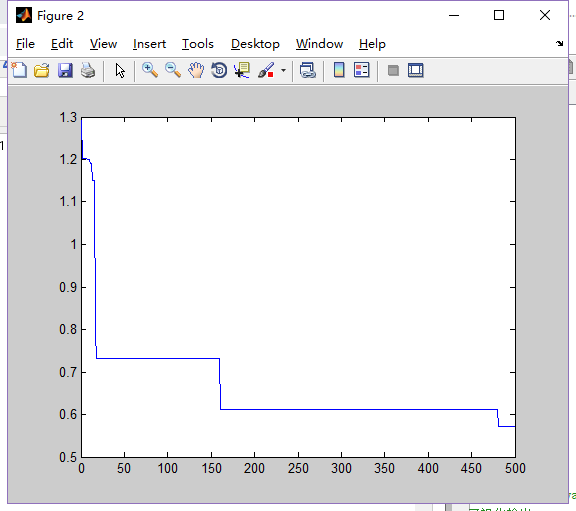
六、运行结果

1.Dim=5,N=50

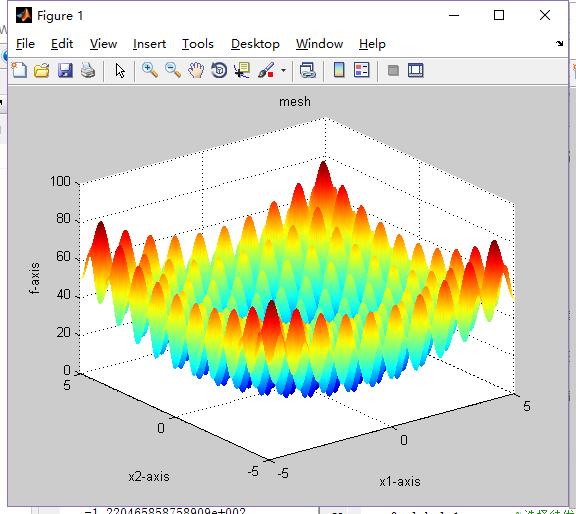
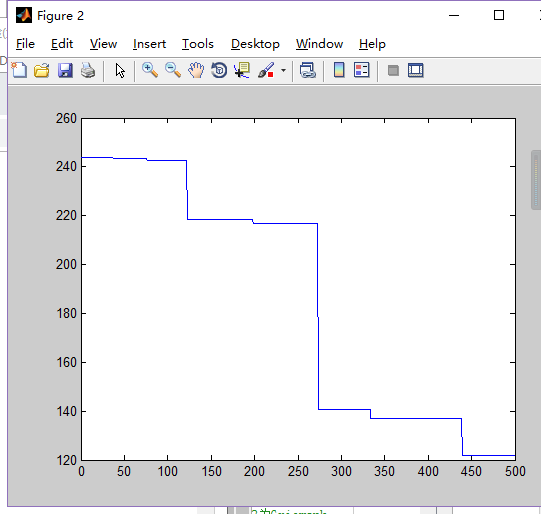
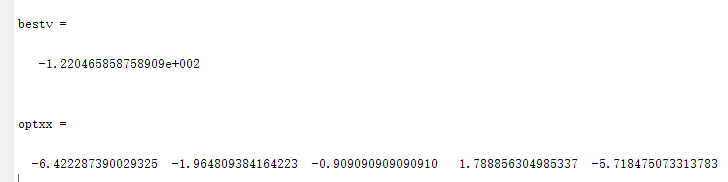
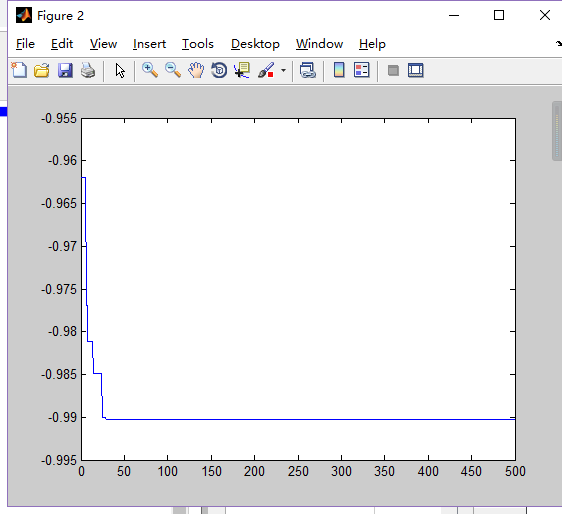
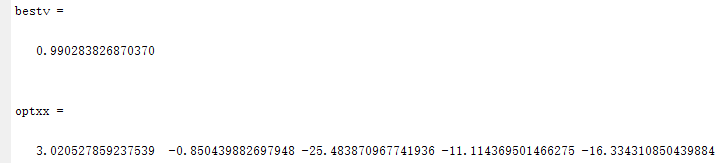
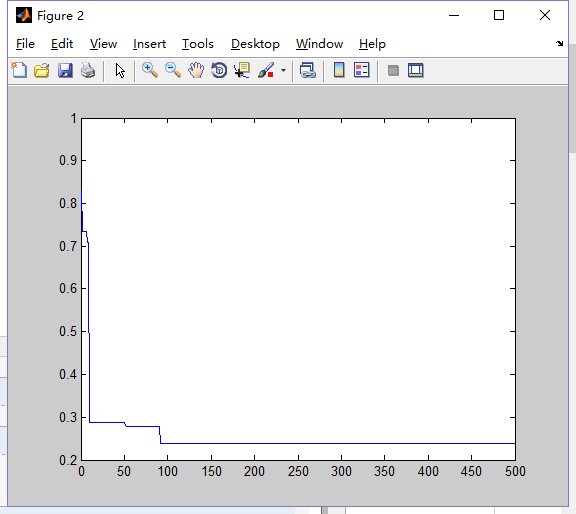
2.Dim=5,N=80

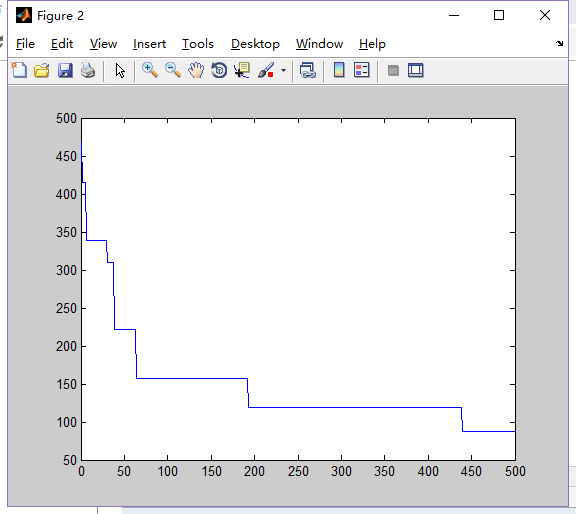
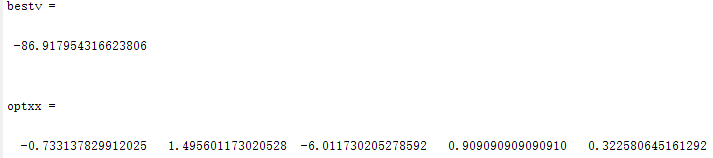
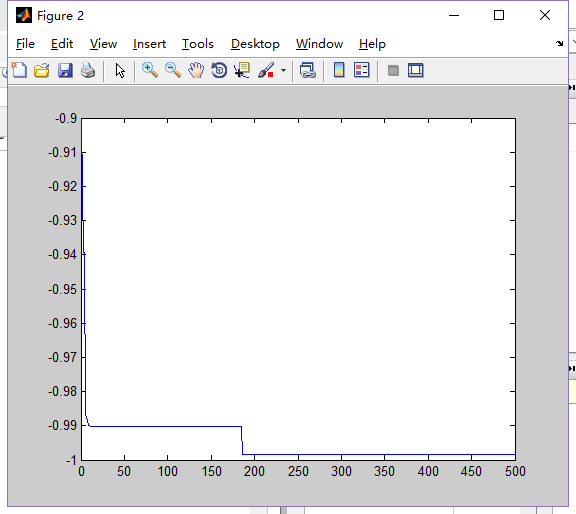
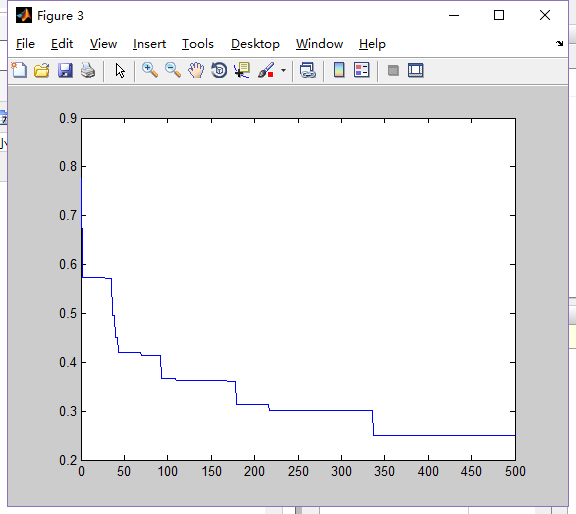
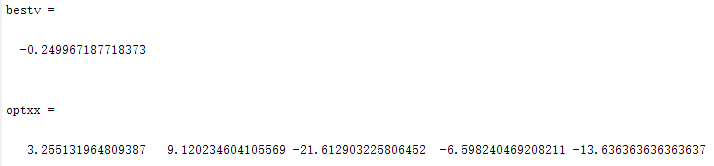
3.Dim=10,N=80

七、结论

1.随着种群规模N的增大，算法的时间将增大；当维度dim增大，算法的时间增大；

2.每次结果可能不一样，遗传算法具有随机性。

3.种群规模N增大时，全局搜索能力强，但是收敛速度变慢。

4.种群规模和维度相比，种群规模影响更大，因为再进行选择，交叉等基本操作中几乎得遍历一遍种群。