The Rotation Game （POJ 2286） 题解

【问题描述】

（由于是英文的，看不懂，这里就把大意给大家说一下吧……都是中国人，相信大家也不愿意看英文……）

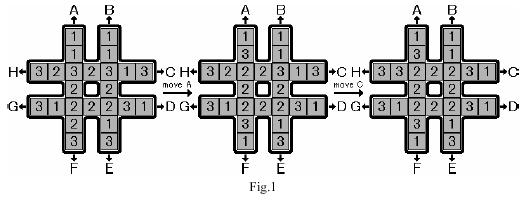
如图，一个井字形的棋盘，中间有着1-3任意的数，有ABCDEFGH八个操作，每个操作意味着该操作所在行朝该操作方向整体移动一格，详见图，你的目的是：对于输入的多组数据，用最少的步数使得井字形棋盘中间的八个数为同一个数，若不需操作就已达到要求，则输出“No moves needed”，无论是否需要操作，你都应将中间的数字给输出。输入以一个0结束。

【样例输入】

1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3

1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3

0

【样例输出】

AC

2

DDHH

2

【解题思路】

又是一道求最少步数的题目……果断写广搜，然而，写完广搜后，我奇迹般地发现……MLE了…………………………空间只给了150MB，我再一看时间………………15000ms……也不想多说什么了，赶紧用上今天刚学的IDA*算法。

IDA*算法是一种将估价函数与深搜结合的搜索方法，搜索方式是用深度优先搜索的方式，搜完第k层若还没有结果，那么就退出，然后从第一层开始搜到第k+1层，不断加深所搜的层数，因此又叫迭代加深搜索。其实说这么复杂，按我的理解，就是用深搜来做的广搜……

现在我们来看一下题目。因为是井字型棋盘，且输入还是一行数，那么，我们就给棋盘上的数标上号，分别为1-24，那么八个移动的过程也可以表示出来了，然后由于是深搜，那么就还有回溯的过程，对于每一个操作，都需要一个反操作，而题目中正好又提示了我们，A的反操作是F等等，因此，我们只需要记录每个操作的反操作是第几个就行了。

然后是边界条件，这里的边界条件是当搜索层数大于当前所设置的最大深度限制时，便退出，实际上每一个迭代加深搜索都有这个边界条件，而另外的边界条件则因题目而异，这道题则不需要其他的边界条件，满足要求退出即可。

接下来考虑初始化的问题，我们在找中间的值的时候，自然是要找最多的数，然后将其他的数移成这个数就行了，那么估价函数就是8-最大的数的个数，从这个估价函数的层数开始搜索，详见代码。

【代码实现】

 const xh:array[..,..] of longint=((,,,,,,),(,,,,,,),(,,,,,,),(,,,,,,),(,,,,,,),(,,,,,,),(,,,,,,),(,,,,,,));
       fan:array[..] of longint=(,,,,,,,);
       op:array[..] of char=('A','B','C','D','E','F','G','H');
       mid:array[..] of longint=(,,,,,,,);
 var n,m,dep:longint;
     s:array[..] of longint;
     a:array[..] of longint;
     i,j:longint;
 function max(a,b,c:longint):longint;
 begin
  max:=a;
  if b>max then
   max:=b;
  if c>max then
   max:=c;
 end;
 function get:longint;
 var i:longint;
     cnt:array[..] of longint;
 begin
  fillchar(cnt,sizeof(cnt),);
  for i:= to  do
   inc(cnt[s[mid[i]]]);
  exit(-max(cnt[],cnt[],cnt[]));
 end;
 procedure move(k:longint);
 var i,t:longint;
 begin
  t:=s[xh[k,]];
  for i:= to  do
   s[xh[k,i]]:=s[xh[k,i+]];
  s[xh[k,]]:=t;
 end;
 function dfs(k:longint):boolean;
 var i,h:longint;
 begin
  if k>=dep then
   exit(false);
  for i:= to  do
   begin
    move(i);//移动
    a[k]:=i;
    h:=get;//求最多的数的个数
    if h= then exit(true);
    if (k+h<dep)and(dfs(k+)) then//深搜
     exit(true);
    move(fan[i]);//回溯
   end;
  exit(false);
 end;
 begin
  read(s[]);
  while s[]<> do
   begin
    for i:= to  do
     read(s[i]);
    dep:=get;
    if dep= then
     begin
      writeln('No moves needed');//所给数据本就满足要求，输出，退出
      writeln(s[]);
      read(s[]);
      continue;
     end;
    while not(dfs()) do//如果不满足要求，加深层数，再进行深搜
     inc(dep);
    for i:= to dep- do
     write(op[a[i]]);
    writeln;
    writeln(s[]);
    read(s[]);
   end;
 end.