POJ 1523 SPF（寻找关节点）

                                                                     SPF

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 8155		Accepted: 3730

Description

Consider the two networks shown below. Assuming that data moves around these networks only between directly connected nodes on a peer-to-peer basis, a failure of a single node, 3, in the network on the left would prevent some of the still available nodes from communicating with each other. Nodes 1 and 2 could still communicate with each other as could nodes 4 and 5, but communication between any other pairs of nodes would no longer be possible.

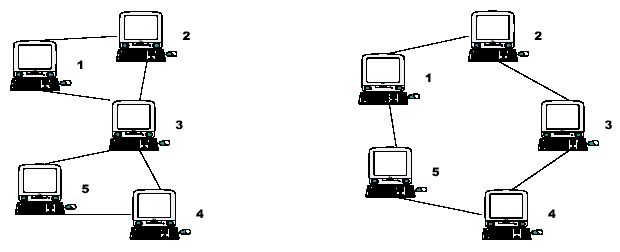
Node 3 is therefore a Single Point of Failure (SPF) for this
network. Strictly, an SPF will be defined as any node that, if
unavailable, would prevent at least one pair of available nodes from
being able to communicate on what was previously a fully connected
network. Note that the network on the right has no such node; there is
no SPF in the network. At least two machines must fail before there are
any pairs of available nodes which cannot communicate.

Input

The
input will contain the description of several networks. A network
description will consist of pairs of integers, one pair per line, that
identify connected nodes. Ordering of the pairs is irrelevant; 1 2 and 2
1 specify the same connection. All node numbers will range from 1 to
1000. A line containing a single zero ends the list of connected nodes.
An empty network description flags the end of the input. Blank lines in
the input file should be ignored.

Output

For each network in the input, you will output its number in the file, followed by a list of any SPF nodes that exist.

The first network in the file should be identified as "Network #1",
the second as "Network #2", etc. For each SPF node, output a line,
formatted as shown in the examples below, that identifies the node and
the number of fully connected subnets that remain when that node fails.
If the network has no SPF nodes, simply output the text "No SPF nodes"
instead of a list of SPF nodes.

Sample Input

1 2
5 4
3 1
3 2
3 4
3 5
0

1 2
2 3
3 4
4 5
5 1
0

1 2
2 3
3 4
4 6
6 3
2 5
5 1
0

0

Sample Output

Network #1
  SPF node 3 leaves 2 subnets

Network #2
  No SPF nodes

Network #3
  SPF node 2 leaves 2 subnets
  SPF node 3 leaves 2 subnets

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <string>
#include <map>
#include <queue>
#include <vector>
#define inf 0x7fffffff
#define met(a,b) memset(a,b,sizeof a)
typedef long long ll;
using namespace std;
const int N = ;
const int M = ;

int edg[N][N],vis[N];
int nodes,tmpdfn,son;
int dfn[N],low[N],subnets[N];
void init()
{
    low[]=dfn[]=;
    tmpdfn=;son=;
    met(vis,);met(subnets,);
    vis[]=;
}
void Tarjan(int u)
{
    for(int v=;v<=nodes;v++){
        if(edg[u][v]){
            if(!vis[v]){
                vis[v]=;
                dfn[v]=low[v]=++tmpdfn;
                Tarjan(v);
                low[u]=min(low[u],low[v]);
                if(low[v]>=dfn[u]){
                    if(u!=)subnets[u]++;
                    else son++;
                }
            }
            else low[u]=min(low[u],dfn[v]);
        }
    }
}
int main()
{
    int u,v,num=;
    while(~scanf("%d",&u)&&u){
        met(edg,);nodes=;
        scanf("%d",&v);
        nodes=max(max(u,v),nodes);
        edg[u][v]=edg[v][u]=;
        while(){
            scanf("%d",&u);
            if(!u)break;
            scanf("%d",&v);
            nodes=max(max(u,v),nodes);
            edg[u][v]=edg[v][u]=;
        }
        if(num>)printf("\n");
        printf("Network #%d\n",num);num++;
        init();
        Tarjan();
        if(son>)subnets[]=son-;
        bool find=false;
        for(int i=;i<=nodes;i++){
            if(subnets[i]){
                find=true;printf("  SPF node %d leaves %d subnets\n",i,subnets[i]+);
            }
        }
        if(!find)printf("  No SPF nodes\n");
    }
    return ;
}