【RL系列】Multi-Armed Bandit问题笔记

这是我学习Reinforcement Learning的一篇记录总结，参考了这本介绍RL比较经典的Reinforcement Learning: An Introduction (Drfit) 。这本书的正文部分对理论的分析与解释做的非常详细，并且也给出了对结论详尽的解析，但是把问题的解决和实现都留到到了课后题，所以本篇文章主要侧重与对Multi-Armed Bandit问题解决算法的实现以及对实现中可能遇到的问题进行一个总结与记录。此外，如果困于书中对于理论解释的冗长，可以参考下面这两篇文章（推荐阅读顺序为：书 → 下面这两篇 → 本篇）：

从Multi-arm Bandits问题分析 - RL进阶

《Reinforcement Learning》读书笔记 2：多臂Bandit（Multi-armed Bandits）

问题分析

Multi-Armed Bandit问题是一个十分经典的强化学习(RL)问题，翻译过来为“多臂抽奖问题”。对于这个问题，我们可以将其简化为一个最优选择问题。

假设有K个选择，每个选择都会随机带来一定的收益，对每个个收益所服从的概率分布，我们可以认为是Banit一开始就设定好的。举个例子，对三臂Bandit来说，每玩一次，可以选择三个臂杆中的任意一个，那么动作集合Actions = [1, 2, 3]，这里的1、2、3分别表示一号臂杆，二号臂杆和三号臂杆。掰动一号号臂杆时，获得的收益服从均匀分布U(-1, 1)，也就是说收益为从-1到1的一个随机数，且收益的均值为0。那么二号臂杆和三号臂杆也同样有自己收益的概率分布，分别为正态分布N(1, 1)和均匀分布U(-2, 1)。这里所需要解决关键问题就是，如何选择动作来确保实验者能获得的收益最高。

我们可以从收益的概率分布上发现二号臂杆的收益均值最高，所以每次实验拉动二号即可，最优选择即为二号。但是对于实验者来说收益概率分布是个黑箱，并不能做出直接判断，所以我们使用RL来估计出那个最优的选择。

算法实现

这里以Sample Average Epsilon-greedy算法为例，给出RL解决Multi-Armed Bandit问题的大致框架：

1. 随机生成收益均值序列，这里我们假设所有选择对应的收益概率分布均为方差相同的正态分布，只不过各个分布的均值不一，这里使用Matlab代码来进行解释

% 10-Armed Bandit

K = 10;

AverReward = randn([1 K]);

% Reward for each Action per experiment

% Reward(Action) = normrnd(AverReward(Action), 1);

2. 依据epsilon-greedy判断当前应当选择的动作。在每次实验开始时，随机一个大于0小于1的值，如果该值小于epsilon，则随机选择动作；如果大于，选择当前平均收益最高的那个动作。

N = 1000 % 1000 experiments

for n = 1:N

    [max i] = max(Q);

    if(max~=0 & rand(1) < 1 - epsilon)

        Action = i;

    else

        Action = unidrnd(K);

    end

    % Q is a set of records of current average reward.

    % Action is in {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

    % Q(1) represents current average reward for action = 1.

end

3. 使用增量形式实现更新当前平均收益Q值

N = 1000 % 1000 experiments

for n = 1:N

    [max i] = max(Q);

    if(max~=0 & rand(1) < 1 - epsilon)

        Action = i;

    else

        Action = unidrnd(K);

    end

    % Q is a set of records of current average reward.

    % Action is in {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

    % Q(1) represents current average reward for action = 1.

　　

    Reward(Action) = normrnd(AverReward(Action), 1);

    N(Action) = N(Action) + 1;

    Q(Action) = (Reward(Action) - Q(Action))*(1/N(Action)) + Q(Action);

end

评价指标

依据 Reinforcement Learning: An Introduction (Drfit) 中关于这一部分的结论分析，主要的两个评价指标是Average Reward和Optimal Action Rate。这两个指标都是用来评价不同算法的优劣程度的。这里的Average Reward和先前提到的当前收益均值是有所不同的。参照上一部分算法实现中给的例子，每次学习过程需要进行1000次实验，每次学习完成后则会得到一个最优估计值，将最优估计值Q记录下来并进行下一次学习，当进行n次学习后，评价收益均值即为这n个Q值的均值，给出Average Reward的计算方法：

$Average\ Reward = \frac{\sum Q}{n}\\$

需要注意的是，在计算Average Reward(AR)时，各动作的收益概率分布需要保持不变。不同的算法得到的AR值也不同，通常来说一个算法的AR值越高表明依据该算法获得的最优估计值与实际的最优值间的差距越小，简单来说就是该算法的可靠性越高。

Optimal Action Rate(OAR) 表示最佳动作选择率，当进行多次学习时，计算最优估计值与实际最优值速对应的动作相符的频率，将其近似为一个算法的OAR。通常来说，一个算法的OAR越高，说明该算法估计的成功率越高，稳定性越好。

这里给出不同epsilon值所对应不同的epsilon-greedy算法的AR与OAR的对比。下面先给出实验的具体参数设置：

10-Armed Bandit，也就是说K = 10
Epsilon = [0 0.01 0.1 1]
收益服从正态分布N(Reward(Action), 1)
每次学习实验次数为500次
学习次数为500次

下图给出了随着实验次数的增加，Average Reward的变化图像：

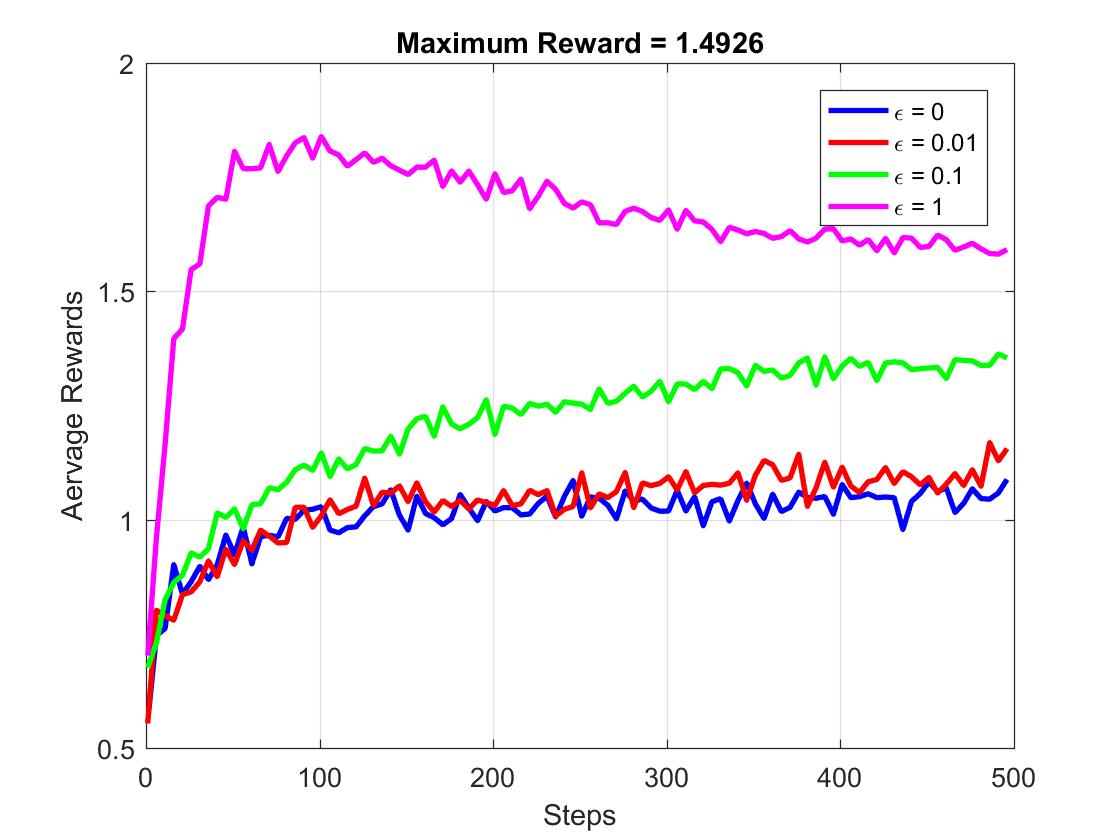
后续请关注：https://blog.csdn.net/baidu_37355300/article/details/80869577