2019PKU\THU WC题解

PKU:

机试：

d1t1：

考虑拓扑序的合法性，每个点的入边必须先加入。f[S]表示先出来的是S集合的点，对应边的方案数。加入x的时候，把入边方向确定，出边自然后面会确定的

2^n*n

d1t2：

虚树，点数=边数+1，NTT，

先咕咕咕

d1t3：

地主斗。。。

炸弹，火箭先处理

剩下牌的特征值（每个方式最大的），以及对应的牌数

hash表存一下

然后再找B的

特征值要状压，还要边加入边计算特征值。

d2t1：

a[i]=0的部分分：

分成n段

每个点在每个段的方案数有相同之处

f[i][j]表示前i个，第i个取再前j段的前缀和

转移的时候

枚举最左边选择j的l

l到i的部分就是盒子放球的问题

据说是APIO赛艇弱化版0？

满分：

区间dp

dp[i][l][r]，前i高位，确定了[l],[r]方案数

还要什么数位dp记录0/1

咕咕咕咕

d2t2：

两个环有公共边，

一定在一个SCC里

反之，可能八字图情况，在SCC里，却没有公共边

先求出SCC

再在SCC中求出点双连通分量个数，和就是ans

SCC中不是V-DCC的环坑定没有公共边

SCC中的V-DCC一定还是SCC

而且没有上面的情况了

所以就是一个联通块

d2t3

每个圆被完全覆盖就可以删掉

n^2*m部分分

两种方法：

①圆的面积并

②对于i，找到最左最右的圆和i的交的角度

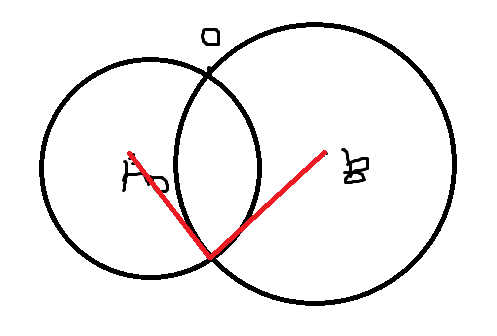
记录红色角的最大值

左边同理

如果角相互有覆盖，A0就被覆盖了

发现所有剩下的点

都在{A0,A1,,,An,O}组成的凸包上

而且是严格的，也即不会存在一个点在凸包的边上

简单证明：

对于共线的三个点，中间的一定可以删除

对于和A，O共线并且在A,O中间的点一定可以删除

对于凸包内部的点一定可以删除

凸包上的点一定删不掉

O是变化的

对于{Ai}先建立凸包

每个O

1.判断O是不是在凸包内部或者边上

　　方法可以是：求x往下的射线和凸包交点的个数，把凸包劈成上下两个部分，分别二分出经过该射线的凸包的边，看有没有交即可。

如果在内部，直接输出凸包点的个数即可。

2.如果O在凸包外部

二分包住的部分删掉。

　　方法可以是：

　　劈成上下两个部分

　　对O分四种情况讨论

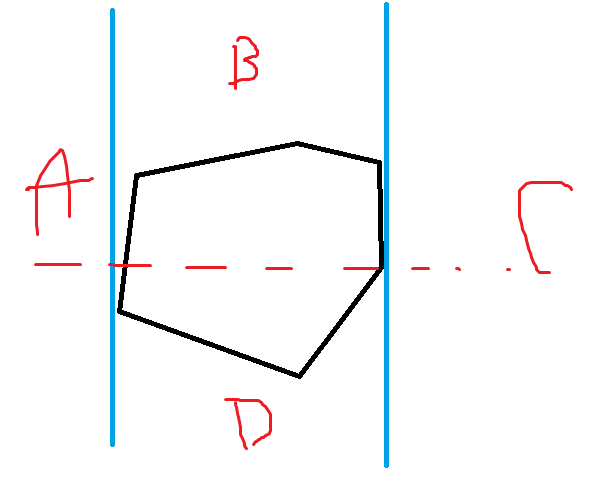
对于B，D位置，直接对上/下凸壳二分即可

对于A，C位置，对上下两个凸壳分分别二分找到第一个和下一个边的叉积为正的点，删掉中间的点即可

O(nlogn+mlogn)

数学：

10个填空题，150min

T1：

8个点的树，2个点度数3,2个点度数2,4个点度数1

求不同的树的个数（定义为，编号a和编号b之间的边存在情况都相同才相同）

prufer序列，暴力枚举生成树然后判断

或者考虑度数为3的点的连接情况，分类讨论+hash（hash不能随便写，所有的边排序之后，i是第i条边，大概用(x*131+y)*i*(i^(i*233)这种越复杂越好，多个hash也可以）

T2：

单位立方体ABCD-A'B'C'D'，从A到C'，只能走棱，或者面的对角线

路径不能自交（包括点，棱上）

求A到C'的最长路

3+4sqrt(2)

最多走7次

可以对顶点黑白染色

对角线走到同色点，棱走到异色点

A，C'不同色，所以走奇数次棱

由于1+6sqrt(2)不存在方案

所以3+4sqrt(2)最优

THU

d1t1：

原题：bzoj5016一个简单的询问

推式子，考虑每一个信封在所有情况中的贡献之和

就是sum1k*sum2k

可以把询问二维差分一下

莫队搞定

d1t2：

每个铁路的开通时间计算出来，

整体二分+bfs处理分治

考虑有没有铁路网，大力分情况讨论

d2t1：

主席树智障送分题

d2t2：

部分分：

n ^2询问任意两个点，看总距离是否为1，确定有无树边

次数小于1000000?

rand一个根，再n-1次询问，找到每个点的深度

深度相差1的才询问

乱搞，可以过。

d2t3：

就是找所有凸包的方案数，面积和，面积平方和

三者本质都相同

考虑求凸包的过程——先要找到左下角的点

枚举左下角的点x

其他x右上方的点按照和x的极角排序

f[i][j][k]表示，前i个点，凸包最后一个是j，倒数第二个是k，枚举下一个是否加入即可

O(n*n^3)

考虑枚举i之后，

g[j][k]表示，最后一个是j，倒数第二个是k的答案

固定j，把剩下的点按照对j的极角序排序

可以双指针，一个枚举t，一个枚举k

把g[j][k]转移到g[t][j]

复杂度O(n*n^2)