堆排序详解以及java实现

前言

临近毕业，开始找工作，近期一直在看算法导论（CLRS）同时各种刷题。希望以后有时间把所有学习心得和刷题心得记录下来。

堆

堆排序和合并排序一样，是一种时间复杂度为O(nlgn)的算法，同时和插入排序一样，是一种就地排序算法(不需要额外的存储空间)。堆排序需要用到一种被称为最大堆的数据结构，与java或者lisp的gc不一样，这里的堆是一种数据结构，他可以被视为一种完全二叉树，即树里面除了最后一层其他层都是填满的。也正是因为这样，树里面每个节点的子女和双亲节点的序号都可以根据当前节点的序号直接求出。

Parent(i)=i/2

Left(i)=2*i

Right(i)=2*i+1

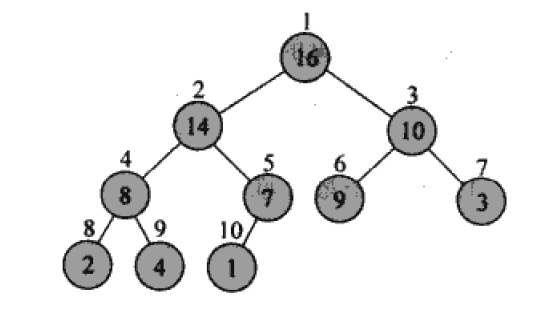
如上图所示，1位置的子女节点分别为2,3  2节点的子女节点为4,5 2的双亲节点为1 考察其他节点也很容易发现上述关系。最大堆是一种特殊的堆，其特点是每个双亲节点的值都比子女节点大。他的这一特点使得他可以实现nlgn的就地排序。现在我们先来看看怎么构建和保持一个最大堆。

最大堆的构建和保持

我们现在有一个数组A,大小是n，假设其中元素按照完全二叉树的方式排列。如何将其构造成一个最大堆？首先我们知道最大堆的每个子树都符合最大堆的性质（根节点值大于所有子节点）。同时我们知道序号为（n/2+1）~n的元素都是叶子节点（因为其子女节点的序号都大于n，即说明没有子女节点），因此我们构建最大堆的操作就在序号为1~n/2的元素内进行（其他元素已满足最大堆性质）。我们定义如下操作maxify(i):将以i位置节点为根的子树改造成最大堆。其操作内容如下：对于每个节点i，我们考察他与子女节点的大小，如果他比某个子女节点小，则将他与子女节点中最大的那个互换位置，然后在相应的子女节点位置重复操作，直到到达堆的叶子节点或者考察的位置比子女节点的值都要大为止。由此可知我们构造最大堆buildmaxheap的过程就是在每个内部节点上调用maxify过程，依次到树的根部，此时其左右子树都是最大堆，现在在根节点调用maxify即完成了最大堆的构造。

堆排序的操作

有了最大堆的基础结构后，我们就可以利用最大堆的性质进行排序HeapSort，我们从根节点开始操作，因为根节点是这个数组中最大的元素，因此我们将其于数组中最后一个元素对换（排序后，最大元素应该在最后）将heapsize减1，然后再在根节点出调用maxify过程将新的堆重新最大堆化。依次循环，我们每次都能将现有堆中最大的元素放到堆末尾。最后就完成了整个排序过程。操作情况见下图（只列出了前4步）

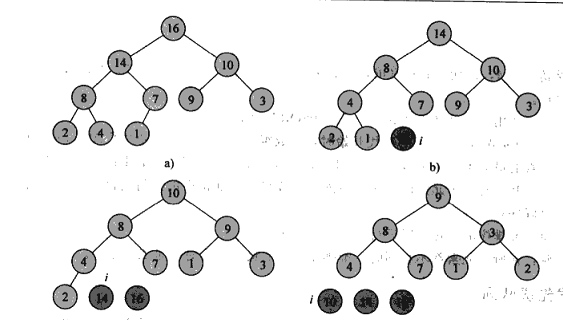
代码及运行结果

public class MaxHeap {
int[] heap;
int heapsize;
public MaxHeap(int[] array)
{
    this.heap=array;
    this.heapsize=heap.length;
}
public void BuildMaxHeap()
{
    for(int i=heapsize/2-1;i>=0;i--)
    {
        Maxify(i);//依次向上将当前子树最大堆化
    }
}
public void HeapSort()
{
    for(int i=0;i<heap.length;i++)
    {
        //执行n次，将每个当前最大的值放到堆末尾
        int tmp=heap[0];
        heap[0]=heap[heapsize-1];
        heap[heapsize-1]=tmp;
        heapsize--;
        Maxify(0);
    }
}
public void Maxify(int i)
{
    int l=Left(i);
    int r=Right(i);
    int largest;

    if(l<heapsize&&heap[l]>heap[i])
        largest=l;
    else
        largest=i;
    if(r<heapsize&&heap[r]>heap[largest])
        largest=r;
    if(largest==i||largest>=heapsize)//如果largest等于i说明i是最大元素 largest超出heap范围说明不存在比i节点大的子女
        return ;
    int tmp=heap[i];//交换i与largest对应的元素位置，在largest位置递归调用maxify
    heap[i]=heap[largest];
    heap[largest]=tmp;
    Maxify(largest);
}
public void IncreaseValue(int i,int val)
{
    heap[i]=val;
    if(i>=heapsize||i<=0||heap[i]>=val)
        return;
    int p=Parent(i);
    if(heap[p]>=val)
        return;
    heap[i]=heap[p];
    IncreaseValue(p, val);
}

private int Parent(int i)
{
    return (i-1)/2;
}
private int Left(int i)
{
    return 2*(i+1)-1;
}
private int Right(int i)
{
    return 2*(i+1);
}
}

public class Demo {
public static void main(String[] args)
{
    int[] array=new int[]{1,2,3,4,7,8,9,10,14,16};
    MaxHeap heap=new MaxHeap(array);
    System.out.println("执行最大堆化前堆的结构：");
    printHeapTree(heap.heap);
    heap.BuildMaxHeap();
    System.out.println("执行最大堆化后堆的结构：");
    printHeapTree(heap.heap);
    heap.HeapSort();
    System.out.println("执行堆排序后数组的内容");
    printHeap(heap.heap);

}
private static void printHeapTree(int[] array)
{
    for(int i=1;i<array.length;i=i*2)
    {
        for(int k=i-1;k<2*(i)-1&&k<array.length;k++)
        {
            System.out.print(array[k]+" ");
        }
        System.out.println();
    }
}
private static void printHeap(int[] array)
{
    for(int i=0;i<array.length;i++)
    {
        System.out.print(array[i]+" ");
    }
}

}