CSS基础6之盒子模型1
盒子概述
以下是盒子模型的一个图形解释
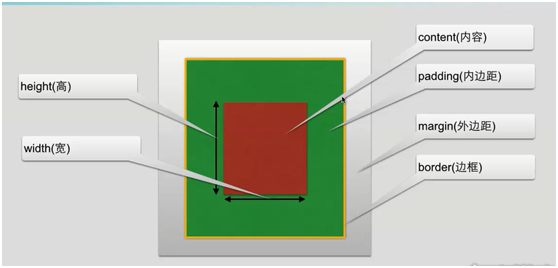
一、内边距（填充）
属性有： (1) padding 设置所有内边距
(2) padding-top 设置上边距
(3) padding-left 设置左边距
(4) padding-right 设置右边距
(5) padding-bottom 设置底边距
如果在设置时：
padding：100px 这代表四个边距都为100px。
内边距例子：
首先我们设置一个div
.neibianju {
width:50px;
height:30px;
background:red;
}
<div class="neibianju">
内边距
</div>
效果如下：
（6）加入左内边距
.neibianju {
width:50px;
height:30px;
background:red;
padding-left:100px;
}
然后我们在通过"开发者选项(F12)"查看，在左边增加了100px的内边距
其他边距同理
二、边框
同样使用上边的代码
.neibianju {
width:50px;
height:30px;
background:red;
padding:100px;
border:5px solid blue;
}
border：边框
5px: 边框宽度为5像素。
solid: 边框为实线
blue：边框颜色为蓝色
下过如下图：
边框为蓝色的
三、外边距属性：margin
控制块与块之间的距离
（1）上下外边距会重叠
比如：上边的块距离下边的块30px，下边的块距离上边的块也30px。结果他们之间的距离不会变成60，还是30px。
例子：
<divstyle="width:300px;height:100px;background:red;margin-bottom:30px"></div>
<divstyle="width:200px;height:100px;background:yellow;margin-top:30px"></div>
（2）div能够实现嵌套，但是子div的margin-top的属性值会传递给父级div。效果就是子盒子不会离父盒子有30px。而是他们俩同时向下移动30px.
可以使用内边距离是子盒子向下移动
注意：尽量少使用外边距
例子：.a {
width:600px;
height:300px;
background:aqua;
border:1px solid aqua;
}
.b {
width:100px;
height:100px;
background:red;
margin-top:30px;
}
<body>
<div class="a">
<div class="b">
</div>
</div>
</body>
正常下效果如下： 将子div设置margin-top效果如下
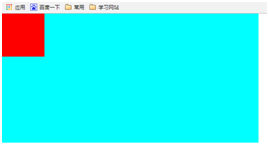
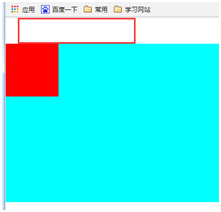
但是在父级div上加入border:1px solid aqua;
子div的margin-top就不会传递给父div。不知道是什么原因效果如下：
上边这种情况称之为:外边距塌陷
首先盒子与盒子之间属于嵌套关系
解决方式
(1)、给父盒子添加border值
但是这样会影响盒子本身的大小。
(2)、给父盒子添加 overflow: hidden;
overflow:hidden: 触发元素的bfc(格式化上下文)
(3)单个盒子的外边距
{margin：0 auto 0 auto}：他始终都是居中的。
简写为：{margin：0 auto;}
CSS基础6之盒子模型1的更多相关文章
- 前端开发：css基础知识之盒模型以及浮动布局。
前端开发:css基础知识之盒模型以及浮动布局 前言 楼主的蛮多朋友最近都在学习html5,他们都会问到同一个问题 浮动是什么东西? 为什么这个浮动没有效果? 这个问题楼主已经回答了n遍.今天则是把 ...
- css的两种盒子模型
css的两种盒子模型:W3C标准盒子模型.IE盒子模型 两者的相同之处:都包含margin.border.padding.content 两者的不同之处:W3C标准盒子模型的content部分不包含其 ...
- CSS Box Model（盒子模型）
CSS Box Model(盒子模型) 一.简介 所有HTML元素可以看作盒子,在CSS中,"box model"这一术语是用来设计和布局时使用. CSS盒模型本质上是一个盒子,封 ...
- [CSS属性设置，盒子模型，网页布局]
[CSS属性设置,盒子模型,网页布局] CSS属性设置 1. 宽和高 width:属性可以为元素设置宽度. height:属性可以为元素设置高度. 块级标签的宽度不修改的情况下默认占浏览器的一整行,块 ...
- CSS魔法堂：盒子模型简介
本文讨论的是块级盒子(Block-level box)的盒子模型(Box Model) 一.W3C标准的盒子模型 二.IE盒子模型 三.两种模型的区别 W3C标准盒子模型: 外盒模型 元素空间宽度 ...
- css那些事儿2 盒子模型
盒子模型是网页元素所占据页面窗口的矩形范围,是网页布局的核心基础之一,这里的盒子模型与我们平常收到的包裹类似. 一个包裹从内到外,分为真实物品部分,物品与外壳之间的填充区,外壳的厚度,当多个包裹放置在 ...
- CSS——（2）盒子模型与标准流
上篇博客<CSS--(1)基础>中简单介绍了CSS的概念和几种使用方法,现在主要是介绍其的核心内容. 盒子模型 为了理解盒子模型,我们可以先从生活中的盒子入手.盒子是用来放置物品的,内部除 ...
- CSS核心概念之盒子模型
盒子模型(Box Model) 关于更多CSS核心概念的文章请关注GitHub--CSS核心概念. 当对一个文档进行布局的时候,浏览器的渲染引擎会根据标准之一的 CSS 基础框盒模型(CSS basi ...
- 【转】CSS（10）盒子模型
CSS中, Box Model叫盒子模型(或框模型),Box Model规定了元素框处理元素内容(element content).内边距(padding).边框(border) 和 外边距(marg ...
随机推荐
- 项目cobbler+lamp+vsftp+nfs+数据实时同步（inotify+rsync)
先配置好epel源 [root@node3 ~]#yum install epel-release -y 关闭防火墙和selinux [root@node3 ~]#iptables -F [root@ ...
- spring Profile 为不同环境提供不同的配置支持
说明 Profile为在不同环境下使用不同的配置提供了支持(开发环境下的配置和生产环境下的配置肯定是不同的, 例如, 数据库的配置) . 在spring开发中用@Profile 注解使用来选择行配置系 ...
- 【模型推理】Tengine 模型转换及量化
欢迎关注我的公众号 [极智视界],回复001获取Google编程规范 O_o >_< o_O O_o ~_~ o_O 本文介绍一下 Tengine 模型转换 ...
- Mysql配置文件 16c64g优化
目录 一.说明 二.配置 一.说明 以下配置适合16核64G及以上的配置,会让性能稍微提高1/3左右. 二.配置 my.cnf [client] port = 3306 socket = /usr/l ...
- Mybatis动态SQL语句使用
在实际开发中,有时候查询条件可能是不确定的,查询条件可能有多条也可能没有,这时候就需要用到动态的sql语句拼接功能. 一.if.where.sql标签的使用 需求:在一些高级查询中,查询条件存在的个数 ...
- CF1520D Same Differences 题解
Content 给定 \(n\) 个数 \(a_1,a_2,\dots,a_n\),求有多少个二元组 \((i,j)\) 满足: \(i<j\). \(a_j-a_i=j-i\). 数据范围:\ ...
- JAVA里List集合中的对象根据对象的某个属性值降序或者升序排序
需要使用JDK1.8及以上 package com.stream; import java.util.Comparator; import java.util.List; public class T ...
- htmlunit设置只采集html，取消对css,javascript支持
引入htmlunit依赖 <!-- https://mvnrepository.com/artifact/net.sourceforge.htmlunit/htmlunit --> < ...
- c++设计模式概述之适配器
类写的不规范(应该屏蔽类的拷贝构造函数和运算符=).少写点代码,缩短篇幅,重在理解. 实际中可不要这样做. 类比生活中的手机,pad等电源适配器. 简单来讲: 将原本 不匹配 的两者 变的匹配 ...
- 【LeetCode】986. Interval List Intersections 解题报告（C++）
作者: 负雪明烛 id: fuxuemingzhu 个人博客: http://fuxuemingzhu.cn/ 目录 题目描述 题目大意 解题方法 双指针 日期 题目地址:https://leetco ...