Proximal Algorithms 5 Parallel and Distributed Algorithms

问题的结构
consensus
- 更为一般的情况
Exchange 问题
- Global exchange
- 更为一般的情况
Allocation

Proximal Algorithms

这一节，介绍并行算法的实现.

问题的结构

令$[n] = \{1, \ldots, n\}$. 给定$c \subseteq [n]$, 让$x_c \in \mathbb{R}^{|c|}$表示向量$x\in \mathbb{R}^n$的一个子向量(以$c$为指标的对应部分).当$\mathcal{P}=\{c_1, \ldots, c_N\}$满足:

\[\cup \mathcal{P} = [n] \\
c_i \cap c_j = \emptyset, i \ne j
\]

时，称$\mathcal{P}$为$[n]$的一个分割.

函数$f$的$\mathcal{P}-$分割满足:

\[f(x) = \sum_{i=1}^N f_i (x_{c_i})
\]

其中$f_i : \mathbb{R}^{|c_i|} \rightarrow \mathbb{R}$.

在这种情况下:

\[(\mathbf{prox}_f(v))_i = \mathbf{prox}_{f_i}(v_i)
\]

所以，可以并行计算.

考虑下面的问题：

\[\mathrm{minimize} \quad f(x) + g(x)
\]

如果假设$f$是$\mathcal{P}-$分割的, 而$g$是$\mathcal{Q}-$分割的，那么问题等价于:

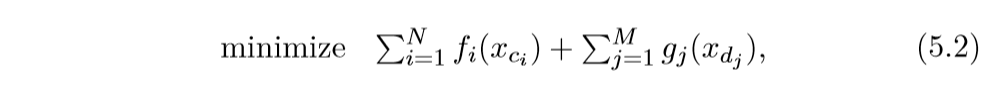
于是ADMM可以并行计算:

consensus

考虑下列问题如何进行并行计算:

\[\mathrm{minimize} \quad f(x) = \sum_{i=1}^N f_i (x)
\]

一个非常巧妙的变化:

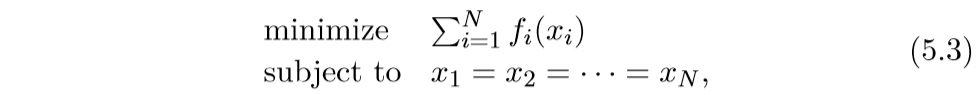
可以看到，这样子，函数就是可分了, 只是多了一个附加条件.

将上面的问题转化为:

\[\mathrm{minimize} \quad \sum_{i=1}^N f_i(x_i) + I_{\mathcal{C}} (x_1, \ldots, x_N)
\]

其中$\mathcal{C}$是consensus set:

\[\mathcal{C} = \{(x_1, \ldots, x_N)| x_1 = \ldots, =x_N\}
\]

这样，问题就变成俩个可分函数了, 不过需要注意的是，二者的分割并不相同:

\[\mathcal{P} = \{[n], n+[n], 2n + [n], \ldots, (N-1)n + [n]\}
\]

而$\mathcal{Q}$，即$I_{\mathcal{C}}$的分割为:

\[\mathcal{Q} = \{\{i, n+i, 2n + i, \ldots, (N-1)n + i\}|i=1, 2, \ldots, n\}
\]

注: 文中是$i=1, 2, \ldots, N$(我认为是作者的笔误).

这个时候的ADMM的第二步，即更新$z$，可以直接为:

\[z_i = \bar{z} = (1/N) \sum_{i=1}^N z_i
\]

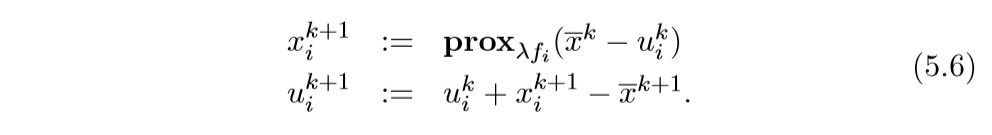
作者贴了一个比较形象的图来表示这种分割:

更为一般的情况

考虑下面的问题:

\[\mathrm{minimize} \quad f(x) = \sum_{i=1}^N f_i (x_{c_i})
\]

其中$c_i \subseteq [n]$，但是$c_i \cap c_j, i \ne j$并不一定为空集.

进行同样的转换:

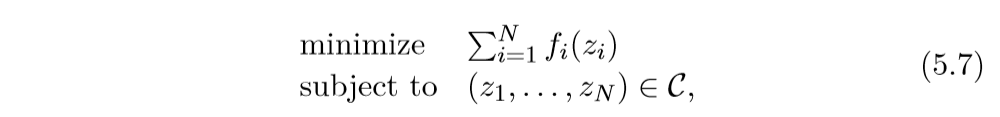
其中

\[\mathcal{C} = \{(z_1, \ldots, z_N) | (z_i)_k = (z_j)_k \quad if \: k \in c_i \cap c_j\}
\]

同样等价于:

\[\mathrm{minimize} \quad \sum_{i=1}^N f_i(z_i) + I_{\mathcal{C}} (z_1, \ldots, z_N)
\]

相应的有一张比较形象的图：

前一部分的分割是类似的, 后一部分的分割，就是怎么说呢，就像图上的行一样的分.

ADMM为:

其中$F_i = \{j \in [N] | i \in c_j\}$

Exchange 问题

Global exchange

交换问题具有如下形式:

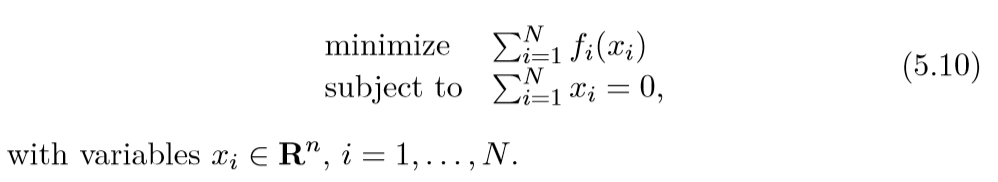
可以用一个实际问题来考量，每个$i$表示一个客户，$x_i$表示每个客户给予或者得到的总量，而$f_i(x_i)$表示该客户的效益，$\sum_{i=1}^Nx_i=0$这个条件表示，所以客户东西的总量是固定的，即收支平衡.

我们可以将此问题转化为(这个方法太好使了吧):

\[\mathrm{minimize} \quad \sum_{i=1}^N f_i(x_i) + I_{\mathcal{C}}(x_1, \ldots, x_N)
\]

其中

\[\mathcal{C} = \{(x_1, \ldots, x_N)\in \mathbb{R}^{nN} | x_1 + x_2 + \ldots + x_N=0\}
\]

我们知道，指示函数的proximal为投影算子, 于是:

\[(\Pi_{\mathcal{C}}(v_1, \ldots, v_N))_i = v_i - \bar{v}
\]

于是ADMM算法为:

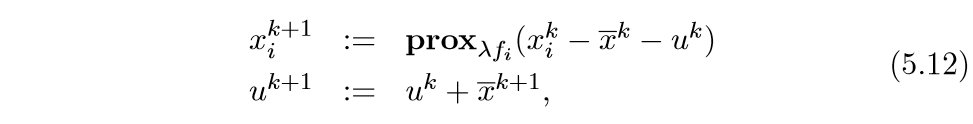
更为一般的情况

有些时候，并不是所有客户都面对同一个市场，所以，每个$x_i$的维度什么对的也有区别:

\[\mathcal{C} = \Big \{ (z_1, \ldots, z_N) \Big| \sum_{i : k \in c_i} (z_i)_k =0 \Big \}
\]

有点和consenus的一般情况比较类似.

Allocation

allocation problem:

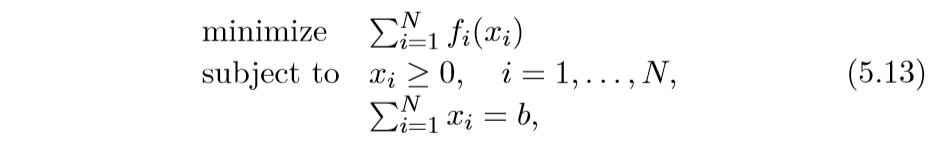
其中$x_i \in \mathbb{R}^n$.

这个问题和交换问题也是相似的，区别在于总量$b$，而且要求$x_i \ge 0$.

类似的，我们可以将上面的问题改写为:

\[\mathrm{minimize} \quad \sum_{i=1}^N f_i(x_i) + I_{\mathcal{C}} (x_1, \ldots, x_N)
\]

其中:

\[\mathcal{C} = \{(x_1, \ldots, x_N)| x_i \ge 0, x_1 + \ldots + x_N = b\}
\]

所以相应的算法是:

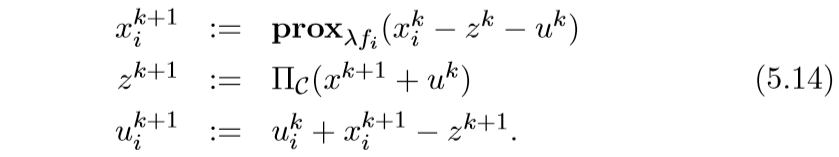
如何进行投影，会在下一节提到，还有更加一般的情况，比如$\sum_{i=1}^N x_i \le b$.