PTA 树的同构 (25分)

PTA 树的同构 (25分)

输入格式:
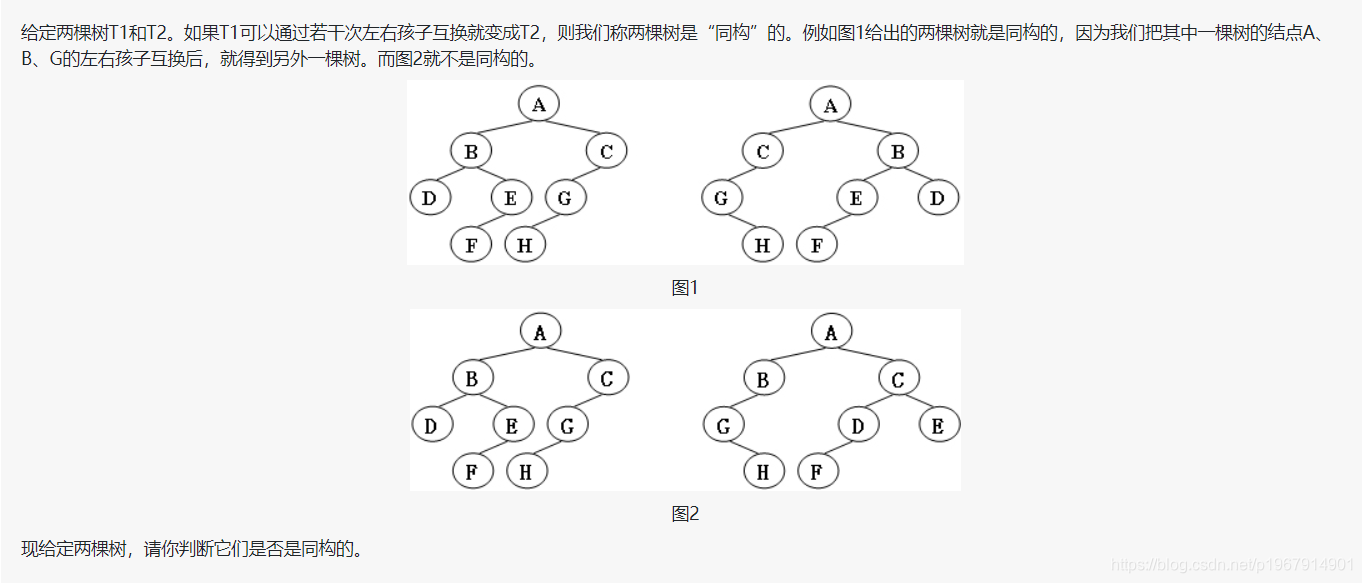
输入给出2棵二叉树树的信息。对于每棵树，首先在一行中给出一个非负整数N (≤10)，即该树的结点数（此时假设结点从0到N−1编号）；随后N行，第i行对应编号第i个结点，给出该结点中存储的1个英文大写字母、其左孩子结点的编号、右孩子结点的编号。如果孩子结点为空，则在相应位置上给出“-”。给出的数据间用一个空格分隔。注意：题目保证每个结点中存储的字母是不同的。
输出格式:
如果两棵树是同构的，输出“Yes”，否则输出“No”。
输入样例1（对应图1）：

8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
8
G - 4
B 7 6
F - -
A 5 1
H - -
C 0 -
D - -
E 2 -

输出样例1:

Yes

输入样例2（对应图2）：

8
B 5 7
F - -
A 0 3
C 6 -
H - -
D - -
G 4 -
E 1 -
8
D 6 -
B 5 -
E - -
H - -
C 0 2
G - 3
F - -
A 1 4

输出样例2:

No

【程序思路】
首先需要根据输入找出根节点，将输入利用静态链表的方式保存，没有被指向的编号就是根节点。再调用函数递归判断树是否同构。
【程序实现】

#include<bits/stdc++.h>
using namespace std;
struct tree{
	int left,right;
	char data;
}a[15],b[15];
int getHhead(struct tree a[]) {
	int n, head = 12, check[15] = {0};
	cin>>n;
	getchar();
	for (int i = 0; i < n; i++) {
		string s;
		getline(cin,s);
		a[i].data = s[0];
		a[i].left = s[2] != '-' ? s[2]-'0' : 12;
		a[i].right = s[4] != '-' ? s[4]-'0' : 12;
		check[a[i].left] = 1;
		check[a[i].right] = 1;
	}
	if(n)
		for (head = 0; head < n;head++)
			if (!check[head]) break;
	return head;
}
bool jdg(int head1, int head2) {
	if(head1 == 12 && head2 == 12)
		return true;
	else if((head1 == 12 && head2 != 12) || (head1 != 12 && head2 == 12))
		return false;
	else if(a[head1].data != b[head2].data)
		return false;
	else if(a[head1].left == 12 && b[head2].left == 12)
		return jdg(a[head1].right, b[head2].right);
	else if(a[head1].left != 12 && b[head2].left !=12 && a[a[head1].left].data == b[b[head2].left].data)
		return (jdg(a[head1].left , b[head2].left) && jdg(a[head1].right , b[head2].right));
	else
		return  jdg(a[head1].left , b[head2].right) && jdg(a[head1].right , b[head2].left);
}
int main(){
	int head1, head2;
	head1 = getHhead(a);
	head2 = getHhead(b);
	if (jdg(head1 , head2))
		cout<<"Yes\n";
	else
		cout<<"No\n";
	return 0;
}