Python小白的数学建模课-18.最小生成树问题

最小生成树（MST）是图论中的基本问题，具有广泛的实际应用，在数学建模中也经常出现。
路线设计、道路规划、官网布局、公交路线、网络设计，都可以转化为最小生成树问题，如要求总线路长度最短、材料最少、成本最低、耗时最小。
最小生成树的典型算法有普里姆算法（Prim算法）和克鲁斯卡算法（Kruskal算法）.
本文基于 NetworkX 工具包，通过例程详细介绍最小生成树问题的求解。
『Python小白的数学建模课 @ Youcans』带你从数模小白成为国赛达人。

1. 最小生成树

1.1 生成树

树是图论中的基本概念。连通的无圈图称为树（Tree），就是不包含循环的回路的连通图。

对于无向连通图，如下图所示，生成树（Spanning tree）是原图的极小连通子图，它包含原图中的所有 n 个顶点，并且有保持图连通的最少的边，即只有足以构成一棵树的 n-1 条边。

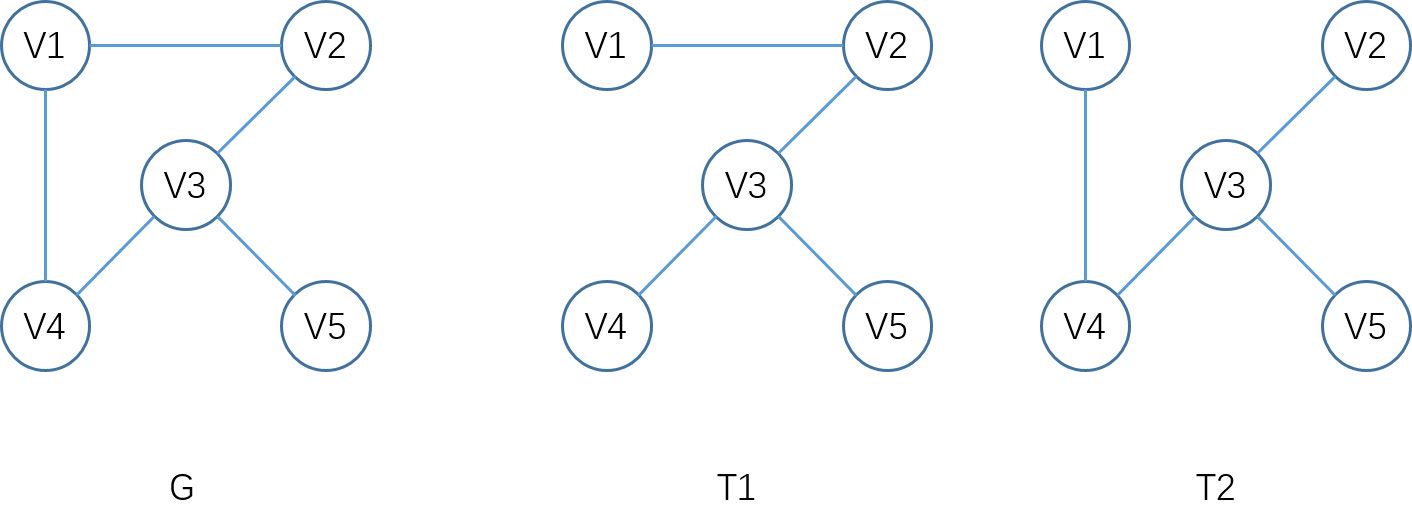
生成树满足：（1）包含连通图中所有的顶点；（2）任意两顶点之间有且仅有一条通路。因此，生成树中边的数量 = 顶点数 - 1。

对于非连通无向图，遍历每个连通分量中的顶点集合所经过的边是多颗生成树，这些连通分量的生成树构成非连通图的生成森林。

1.2 最小生成树和最大生成树

遍历连通图的方式通常有很多种，也就是说一张连通图可能有多种不同的生成树。

无向赋权图的生成树中，各条边的权重之和最小的生成树，称为最小生成树（minimum spanning tree，MST），也称最小权重生成树。

对应地，各条边的权重之和最大的生成树，称为最大生成树（maximum spanning tree）。

1.3 最小生成树问题

最小生成树（MST）是图论中的基本问题，具有广泛的实际应用，在数学建模中也经常出现。

例如，在若干城市之间铺设通信线路，使任意两个城市之间都可以通信，要使铺设线路的总费用最低，就需要找到最小生成树。类似地，路线设计、道路规划、官网布局、公交路线、网络设计，都可以转化为最小生成树问题，如要求总线路长度最短、材料最少、成本最低、耗时最小等。

在实际应用中，不仅要考虑网络连通，还要考虑连通网络的质量和效率，就形成了带有约束条件的最小生成树：

直径限制最小生成树（Bounded diameter minimum spanning tree）：对给定的连通图，满足直径限制的生成树中，具有最小权的树，称为直径限制最小生成树。直径限制最小生成树问题在资源优化问题中应用广泛，如网络设计的网络直径影响到网络的传输速度、效率和能耗。

度限制最小生成树（Degree constrained minimum spanning tree）：对给定的连通图，满足某个节点或全部节点的度约束（如入度不超过 k）的生成树中，具有最小权的树，称为度限制最小生成树。实际应用中，为了控制节点故障对整个系统的影响，需要对节点的度进行限制。

2. 最小生成树算法

构造最小生成树的算法很多，通常是从空树开始，按照贪心法逐步选择并加入 n-1 条安全边（不产生回路），最终得到最小生成树。

最小生成树的典型算法有普里姆算法（Prim算法）和克鲁斯卡算法（Kruskal算法）。

2.1 普里姆算法（Prim算法）

Prim 算法以顶点为基础构造最小生成树，每个顶点只与连通图连接一次，因此不用考虑在加入顶点的过程中是否会形成回路。

算法从某一个顶点 s 开始，每次选择剩余的代价最小的边所对应的顶点，加入到最小生成树的顶点集合中，逐步扩充直到包含整个连通网的所有顶点，可以称为“加点法”。

Prim 算法中图的存贮结构采用邻接矩阵，使用一个顶点集合 u 构造最小生成树。由于不断向集合u中加点，还需要建立一个辅助数组来同步更新最小代价边的信息。

Prim 算法每次选择顶点时，都需要进行排序，但每次都只需要对一部分边进行排序。Prim 算法的时间复杂度为 O(n*n)，与边的数量无关，适用于边很多的稠密图。

采用堆实现优先队列来维护最小点，可以将Prim算法的时间复杂度降低到 O(mlogn)，称为Prim_heap 算法，但该算法的空间消耗很大。

2.2 克鲁斯卡算法（Kruskal算法）

Kruskal 算法以边为基础构造最小生成树，利用避圈思想，每次找到不使图构成回路的代价最小的边。

算法初始边数为 0，每次选择一条满足条件的最小代价边，加入到边集合中，逐步扩充直到包含整个生成树，可以称为“加边法”。

Kruskal 算法中图的存贮结构采用边集数组，权值相等的边在数组中的排列次序是任意的。Kruskal算法开始就要对所有的边进行排序，之后还需要对所有边应用 Union-Find算法，但不再需要排序。

Kruskal 算法的时间复杂度为 O(mlogm)，主要是对边排序的时间复杂度，适用于边较少的稀疏图。

3. NetworkX 的最小生成树算法

3.1 NetworkX 的最小/最大生成树函数

函数	功能
minimum_spanning_tree(G[, weight,...])	计算无向图上的最小生成树
maximum_spanning_tree(G[, weight,...])	计算无向图上的最大生成树
minimum_spanning_edges(G[, algorithm,...])	计算无向加权图最小生成树的边
maximum_spanning_edges(G[, algorithm,...])	计算无向加权图最大生成树的边

3.2 minimum_spanning_tree() 使用说明

minimum_spanning_tree(G, weight='weight', algorithm='kruskal', ignore_nan=False)

minimum_spanning_edges(G, algorithm='kruskal', weight='weight', keys=True, data=True, ignore_nan=False)

minimum_spanning_tree() 用于计算无向连通图的最小生成树（森林）。minimum_spanning_edges() 用于计算无向连通图的最小生成树（森林）的边。

对于连通无向图，计算最小生成树；对于非连通无向图，计算最小生成森林。

主要参数：

G(undirected graph)：无向图。
weight(str)：指定用作计算权重的边属性。
algorithm(string)：计算最小生成树的算法，可选项为 'kruskal'、'prim' 或 'boruvka'。默认算法为 'kruskal'。
data(bool)：指定返回值是否包括边的权值。
ignore_nan(bool) ：在边的权重为 Nan 时产生异常。

返回值：

minimum_spanning_tree() 的返回值是由最小生成树构成的图，类型为 NetworkX Graph，需要用 T.edges() 获得对应的最小生成树的边。
minimum_spanning_edges() 的返回值是最小生成树的构成边，类型为<class 'generator'>，需要用 list() 转换为列表数据。

3.3 案例：天然气管道铺设问题

问题描述：

某市区有 7个小区需要铺设天然气管道，各小区的位置及可能的管道路线、费用如图所示，要求设计一个管道铺设路线，使天然气能输送到各个小区，且铺设管道的总费用最小。

程序说明：

这是一个最小生成树问题，用 NetworkX 的 minimum_spanning_tree() 函数即可求出费用最小的管道路线。

图的输入。本例为稀疏的有权无向图，使用 G.add_weighted_edges_from() 函数以列表向图中添加多条赋权边，每个赋权边以元组 (node1,node2,weight) 表示。
nx.minimum_spanning_tree() 和 nx.tree.minimum_spanning_edges() 都可以计算最小生成树，参数设置和属性也基本一致，区别主要在于返回值的格式和调用方式。

Python 例程：

# mathmodel18_v1.py

# Demo18 of mathematical modeling algorithm

# Demo of minimum spanning tree(MST) with NetworkX

# Copyright 2021 YouCans, XUPT

# Crated：2021-07-10

import numpy as np

import matplotlib.pyplot as plt # 导入 Matplotlib 工具包

import networkx as nx  # 导入 NetworkX 工具包

# 1. 天然气管道铺设

G1 = nx.Graph()  # 创建：空的 无向图

G1.add_weighted_edges_from([(1,2,5),(1,3,6),(2,4,2),(2,5,12),(3,4,6),

                (3,6,7),(4,5,8),(4,7,4),(5,8,1),(6,7,5),(7,8,10)])  # 向图中添加多条赋权边: (node1,node2,weight)

T = nx.minimum_spanning_tree(G1)  # 返回包括最小生成树的图

print(T.nodes)  # 最小生成树的 顶点

print(T.edges)  # 最小生成树的 边

print(sorted(T.edges)) # 排序后的 最小生成树的 边

print(sorted(T.edges(data=True)))  # data=True 表示返回值包括边的权重

mst1 = nx.tree.minimum_spanning_edges(G1, algorithm="kruskal") # 返回最小生成树的边

print(list(mst1))  # 最小生成树的 边

mst2 = nx.tree.minimum_spanning_edges(G1, algorithm="prim",data=False)  # data=False 表示返回值不带权

print(list(mst2))

# 绘图

pos={1:(1,5),2:(3,1),3:(3,9),4:(5,5),5:(7,1),6:(6,9),7:(8,7),8:(9,4)}  # 指定顶点位置

nx.draw(G1, pos, with_labels=True, node_color='c', alpha=0.8)  # 绘制无向图

labels = nx.get_edge_attributes(G1,'weight')

nx.draw_networkx_edge_labels(G1,pos,edge_labels=labels, font_color='m') # 显示边的权值

nx.draw_networkx_edges(G1,pos,edgelist=T.edges,edge_color='b',width=4)  # 设置指定边的颜色

plt.show()

程序运行结果：

[1, 2, 3, 4, 5, 6, 7, 8]

[(1, 2), (1, 3), (2, 4), (4, 7), (4, 5), (5, 8), (6, 7)]

[(1, 2), (1, 3), (2, 4), (4, 5), (4, 7), (5, 8), (6, 7)]

[(1, 2, {'weight': 5}), (1, 3, {'weight': 6}), (2, 4, {'weight': 2}), (4, 5, {'weight': 8}), (4, 7, {'weight': 4}), (5, 8, {'weight': 1}), (6, 7, {'weight': 5})]

[(5, 8, {'weight': 1}), (2, 4, {'weight': 2}), (4, 7, {'weight': 4}), (1, 2, {'weight': 5}), (6, 7, {'weight': 5}), (1, 3, {'weight': 6}), (4, 5, {'weight': 8})]

[(1, 2), (2, 4), (4, 7), (7, 6), (1, 3), (4, 5), (5, 8)]

4. 案例：建设通信网络

4.1 问题描述

在 n 个城市架设 n-1 条线路，建设通信网络。任意两个城市之间都可以建设通信线路，且单位长度的建设成本相同。求建设通信网络的最低成本的线路方案。

（1）城市数\(n\geq10\)，由键盘输入；

（2）城市坐标 x, y 在（0～100）之间随机生成；

（3）输出线路方案的各段线路及长度。

4.2 程序说明

这是一个典型的最小生成树问题。n 个城市构成图的 n 个顶点，任意两个顶点之间都有连接边，边的权值是两个顶点的间距。
nx.complete_graph(n) 可以创建一个全连接图，即任意两个顶点之间都有连接边。

4.3 Python 例程

# mathmodel18_v1.py

# Demo18 of mathematical modeling algorithm

# Demo of minimum spanning tree(MST) with NetworkX

# Copyright 2021 YouCans, XUPT

# Crated：2021-07-10

import numpy as np

import matplotlib.pyplot as plt # 导入 Matplotlib 工具包

import networkx as nx  # 导入 NetworkX 工具包

from scipy.spatial.distance import pdist, squareform

# # 2. 城市通信网络建设

# nCities = input("Input number of cities (n>=10):")

# nCities = int(nCities)

nCities = 20

np.random.seed(1)

xPos = np.random.randint(0, 100, nCities)  # 生成 [0,100) 均匀分布的随机整数

yPos = np.random.randint(0, 100, nCities)  # 生成 Ncities 个城市坐标

posCity = []

G2 = nx.complete_graph(nCities)  # 创建：全连接图

for node in G2.nodes():

    G2.add_node(node, pos=(xPos[node], yPos[node]))  # 向节点添加位置属性 pos

    posCity.append(G2.nodes[node]["pos"])  # 获取节点位置属性 pos

dist = squareform(pdist(np.array(posCity)))  # 计算所有节点之间的距离

for u, v in G2.edges:

    G2.add_edge(u, v, weight=np.round(dist[u][v],decimals=1))  # 向边添加权值 dist(u,v)

T = nx.minimum_spanning_tree(G2, algorithm='kruskal')  # 返回包括最小生成树的图

print("\n城市位置:\n",G2._node)

print("\n通信网络:\n",sorted(T.edges(data=True)))  # data=True 表示返回值包括边的权重

# mst = nx.tree.minimum_spanning_edges(G2, algorithm="kruskal") # 返回最小生成树的边

# for edge in sorted(list(mst)):

#     print(edge)

fig, ax = plt.subplots(figsize=(8, 6))

node_pos = nx.get_node_attributes(G2, 'pos')  # 顶点位置

nx.draw(G2,node_pos,with_labels=True,node_color='c',edge_color='silver',node_size=300,font_size=10,font_color='r',alpha=0.8)  # 绘制无向图

# nx.draw_networkx_labels(G2, node_pos, labels=node_pos, font_size=6, horizontalalignment='left', verticalalignment='top')  # 绘制顶点属性：位置坐标 pos

# edge_col = ['red' if edge in T.edges() else 'silver' for edge in G2.edges()]  # 设置边的颜色

# nx.draw_networkx_edges(G2, node_pos, edge_color=edge_col, width=2)  # 设置指定边的颜色

nx.draw_networkx_edges(G2, node_pos, edgelist=T.edges, edge_color='r', width=2)  # 设置指定边的颜色

edge_weight = nx.get_edge_attributes(T, 'weight')  # 边的权值

nx.draw_networkx_edge_labels(T, node_pos, edge_labels=edge_weight, font_size=8, font_color='m', verticalalignment='top')  # 显示边的权值

plt.axis('on')  # Remove the axis

plt.xlim(-5, 100)

plt.ylim(-5, 100)

plt.show()

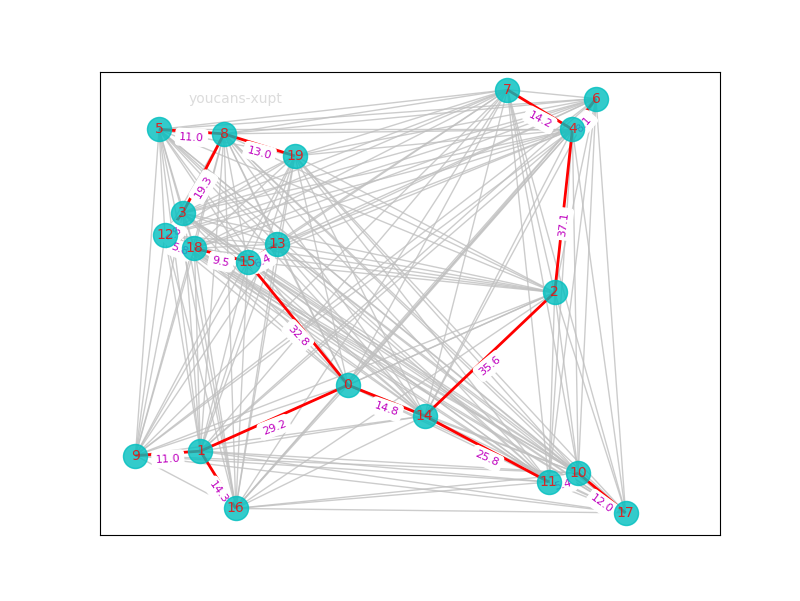
4.4 运行结果

城市位置:

 {0: {'pos': (37, 29)}, 1: {'pos': (12, 14)}, 2: {'pos': (72, 50)}, 3: {'pos': (9, 68)}, 4: {'pos': (75, 87)}, 5: {'pos': (5, 87)}, 6: {'pos': (79, 94)}, 7: {'pos': (64, 96)}, 8: {'pos': (16, 86)}, 9: {'pos': (1, 13)}, 10: {'pos': (76, 9)}, 11: {'pos': (71, 7)}, 12: {'pos': (6, 63)}, 13: {'pos': (25, 61)}, 14: {'pos': (50, 22)}, 15: {'pos': (20, 57)}, 16: {'pos': (18, 1)}, 17: {'pos': (84, 0)}, 18: {'pos': (11, 60)}, 19: {'pos': (28, 81)}}

通信网络:

 [(0, 1, {'weight': 29.2}), (0, 14, {'weight': 14.8}), (0, 15, {'weight': 32.8}), (1, 9, {'weight': 11.0}), (1, 16, {'weight': 14.3}), (2, 4, {'weight': 37.1}), (2, 14, {'weight': 35.6}), (3, 8, {'weight': 19.3}), (3, 12, {'weight': 5.8}), (4, 6, {'weight': 8.1}), (4, 7, {'weight': 14.2}), (5, 8, {'weight': 11.0}), (8, 19, {'weight': 13.0}), (10, 11, {'weight': 5.4}), (10, 17, {'weight': 12.0}), (11, 14, {'weight': 25.8}), (12, 18, {'weight': 5.8}), (13, 15, {'weight': 6.4}), (15, 18, {'weight': 9.5})]

【本节完】

欢迎关注『Python小白的数学建模课 @ Youcans』原创作品

原创作品，转载必须标注原文链接：(https://www.cnblogs.com/youcans/category/1981091.html)。

Crated：2021-07-12

欢迎关注『Python小白的数学建模课 @ Youcans』，每周更新数模笔记

Python小白的数学建模课-01.新手必读

 Python小白的数学建模课-02.数据导入

 Python小白的数学建模课-03.线性规划

 Python小白的数学建模课-04.整数规划

 Python小白的数学建模课-05.0-1规划

 Python小白的数学建模课-06.固定费用问题

 Python小白的数学建模课-07.选址问题

 Python小白的数学建模课-09.微分方程模型

 Python小白的数学建模课-10.微分方程边值问题

 Python小白的数学建模课-12.非线性规划

 Python小白的数学建模课-15.图论的基本概念

 Python小白的数学建模课-16.最短路径算法

 Python小白的数学建模课-17.条件最短路径

 Python小白的数学建模课-18.最小生成树问题

 Python小白的数学建模课-B2.新冠疫情 SI模型

 Python小白的数学建模课-B3.新冠疫情 SIS模型

 Python小白的数学建模课-B4.新冠疫情 SIR模型

 Python小白的数学建模课-B5.新冠疫情 SEIR模型

 Python小白的数学建模课-B6.改进 SEIR疫情模型