【C/C++】例题3-5 生成元/算法竞赛入门经典/数组与字符串

【题目】

x+x的各位数之和为y，x为y的生成元。

求10万以内的n的最小生成元，无解输出0.

【解答】

这是我根据自己的想法最初写的代码：

#include<cstdio>
#include<cstdlib>
#include<cstring>
const int maxn = 100005;
int list[maxn];

int main(){
    int n, m, T;
    memset(list,0,sizeof(list));
    for(m = 1; m < maxn; m++){  //求m加上m的各个数字之和
        int x = 0, y = 0;  //直接对m进行操作，y是累加统计
        while(m>0){
            x = m%10; //最后一位
            y += x;
            m = m/10; //把最后一位去掉
        }
        list[m] = y;
    }
    scanf("%d", &n);
    printf("%d",list[n]);

    system("pause");
}

【DEBUG】

遇到了问题，无法输入，初步判断是在while循环中死循环了。

【原因】因为在循环中修改了计数器m的值。

【修改】将计数器m的值赋值给内部的新变量。



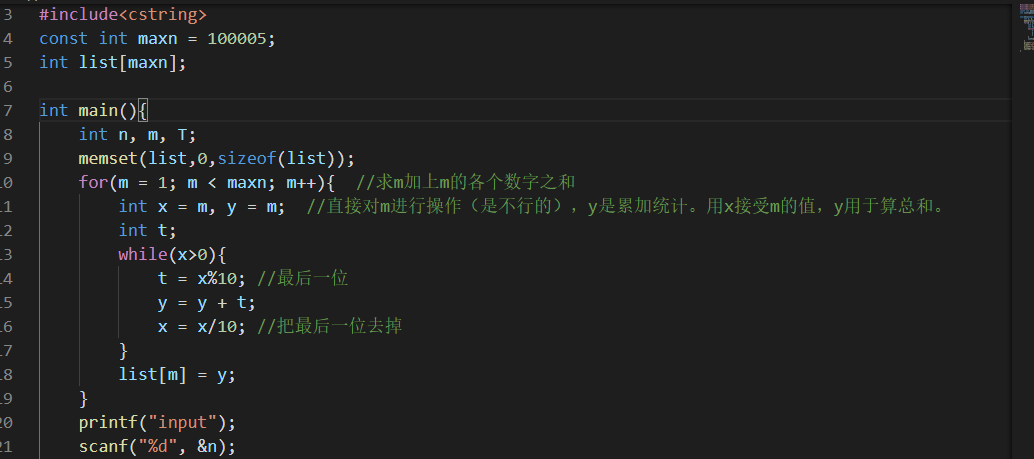
但是这样求出的还是不对。

为什么呢？仔细一看发现是映射关系不对了。

输入的是数字，输出是生成元，利用数组对应关系，应该数组下标是【生成元+各位数之和】，也就是算出来的y才是数组的下标，这个数组的结构是a[y] = m，查询数组下标y的时候才能返回生成元。并且肯定满足【生成元要小于等于数字】。



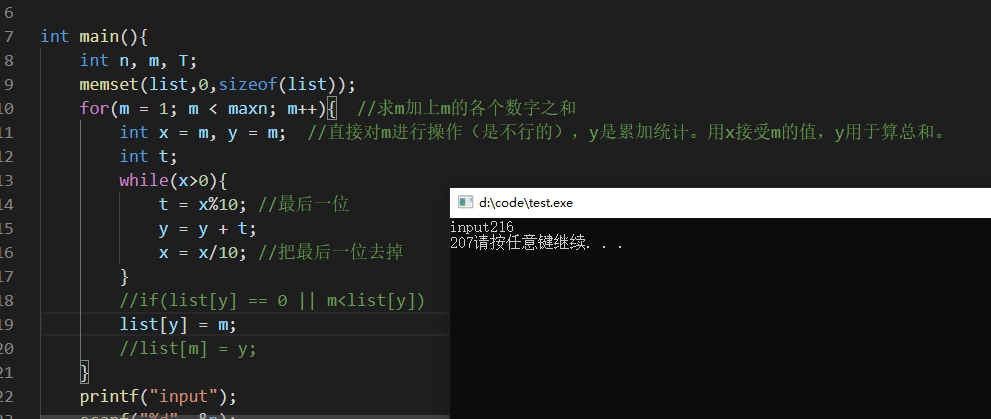
再次将y和m修改之后，依然没法得到正确的结果。

比如，我在输入n=216的时候，输出结果是207，但是正确答案是198. 因为207+2+7=216，198+1+9+8=216.

因为在保存list[y]=m的时候，随着m的增大如果得到了同样的y值，会把list[y]给更新。

因为m是递增的，所以只要保证m是第一次被更新进list中就可以。也就是在更新list[y]=m的之前，判断是否list[y]==0。

另外，关于初始化数组为0，在无解时候要求输出0，相当于无解就没有进行存储，自然就是0了。

限制过输入后，输出符合，但是比起题目中给的例程少了m<list[y]的限制条件。

（这个条件我觉得没啥用，看意思是更新数，但是在递增的情况下感觉没有用处。

（另外源码里，while（T--）的写法我觉得很妙。

#include<cstdio>
#include<cstdlib>
#include<cstring>
const int maxn = 100005;
int list[maxn];

int main(){
    int n, m, T;
    memset(list,0,sizeof(list));
    for(m = 1; m < maxn; m++){  //求m加上m的各个数字之和
        int x = m, y = m;  //直接对m进行操作（是不行的），y是累加统计。用x接受m的值，y用于算总和。
        int t;
        while(x>0){
            t = x%10; //最后一位
            y = y + t;
            x = x/10; //把最后一位去掉
        }
        if(list[y] == 0 || m<list[y]) list[y] = m; //后半句感觉没有什么用
    }
    scanf("%d",&T);
    while (T--)
    {
        scanf("%d",&n);
        printf("%d\n",list[n]);
    }
    system("pause");
}