POJ3398Perfect Service[树形DP 树的最大独立集变形]

Perfect Service

Time Limit: 2000MS		Memory Limit: 65536K
Total Submissions: 1518		Accepted: 733

Description

A network is composed of N computers connected by N − 1 communication links such that any two computers can be communicated via a unique route. Two computers are said to be adjacent if there is a communication link between them. The neighbors of a computer is the set of computers which are adjacent to it. In order to quickly access and retrieve large amounts of information, we need to select some computers acting as servers to provide resources to their neighbors. Note that a server can serve all its neighbors. A set of servers in the network forms a perfect service if every client (non-server) is served by exactly one server. The problem is to find a minimum number of servers which forms a perfect service, and we call this number perfect service number.

We assume that N (≤ 10000) is a positive integer and these N computers are numbered from 1 to N. For example, Figure 1 illustrates a network comprised of six computers, where black nodes represent servers and white nodes represent clients. In Figure 1(a), servers 3 and 5 do not form a perfect service because client 4 is adjacent to both servers 3 and 5 and thus it is served by two servers which contradicts the assumption. Conversely, servers 3 and 4 form a perfect service as shown in Figure 1(b). This set also has the minimum cardinality. Therefore, the perfect service number of this example equals two.

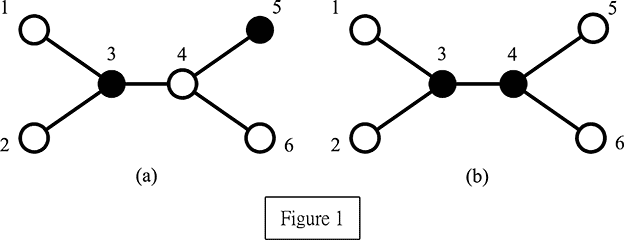
Your task is to write a program to compute the perfect service number.

Input

The input consists of a number of test cases. The format of each test case is as follows: The first line contains one positive integer, N, which represents the number of computers in the network. The next N − 1 lines contain all of the communication links and one line for each link. Each line is represented by two positive integers separated by a single space. Finally, a 0 at the (N + 1)th line indicates the end of the first test case.

The next test case starts after the previous ending symbol 0. A −1 indicates the end of the whole inputs.

Output

The output contains one line for each test case. Each line contains a positive integer, which is 
the perfect service number.

Sample Input

6
1 3
2 3
3 4
4 5
4 6
0
2
1 2
-1

Sample Output

2
1

Source

Kaohsiung 2006

---

题意：选一些节点，使得每个没被选节点恰好与一个被选的节点相邻

---

以u为根的子树有三种情况

f[u][0]表示选自己（son选不选就随便了）

f[u][1]表示选fa，则son不能被选

f[u][2]表示选son中一个，则fa不能被选

转移时f[u][2]可以用加法优化，就是一堆f[v][1]和一个f[v][0]加起来

//
//  main.cpp
//  poj3398
//
//  Created by Candy on 10/14/16.
//  Copyright © 2016 Candy. All rights reserved.
//

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <map>
using namespace std;
const int N=1e4+,INF=1e6;
inline int read(){
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}
int n,u,v;
struct edge{
    int v,ne;
}e[N<<];
int es=,h[N];
inline void ins(int u,int v){
    es++;
    e[es].v=v;e[es].ne=h[u];h[u]=es;
    es++;
    e[es].v=u;e[es].ne=h[v];h[v]=es;
}
int f[N][];//0 i | 1 fa | 2 son
void dp(int u,int fa){//printf("dp %d %d\n",u,fa);
    f[u][]=;f[u][]=;f[u][]=INF;
    for(int i=h[u];i;i=e[i].ne){
        int v=e[i].v;
        if(v==fa) continue;
        dp(v,u);
        f[u][]+=min(f[v][],f[v][]);
        f[u][]+=f[v][];
        f[u][]=min(f[u][],-f[v][]+f[v][]);
    }
    f[u][]+=f[u][];//when finish calc
    //printf("hi %d  %d %d %d\n",u,f[u][0],f[u][1],f[u][2]);
}
int main(int argc, const char * argv[]) {
    while(true){
        n=read();
        if(n==) continue;
        if(n==-) break;
        es=;
        memset(h,,sizeof(h));
        for(int i=;i<=n-;i++){
            u=read();v=read();ins(u,v);
        }
        dp(,);
        printf("%d\n",min(f[][],f[][]));
    }

    return ;
}