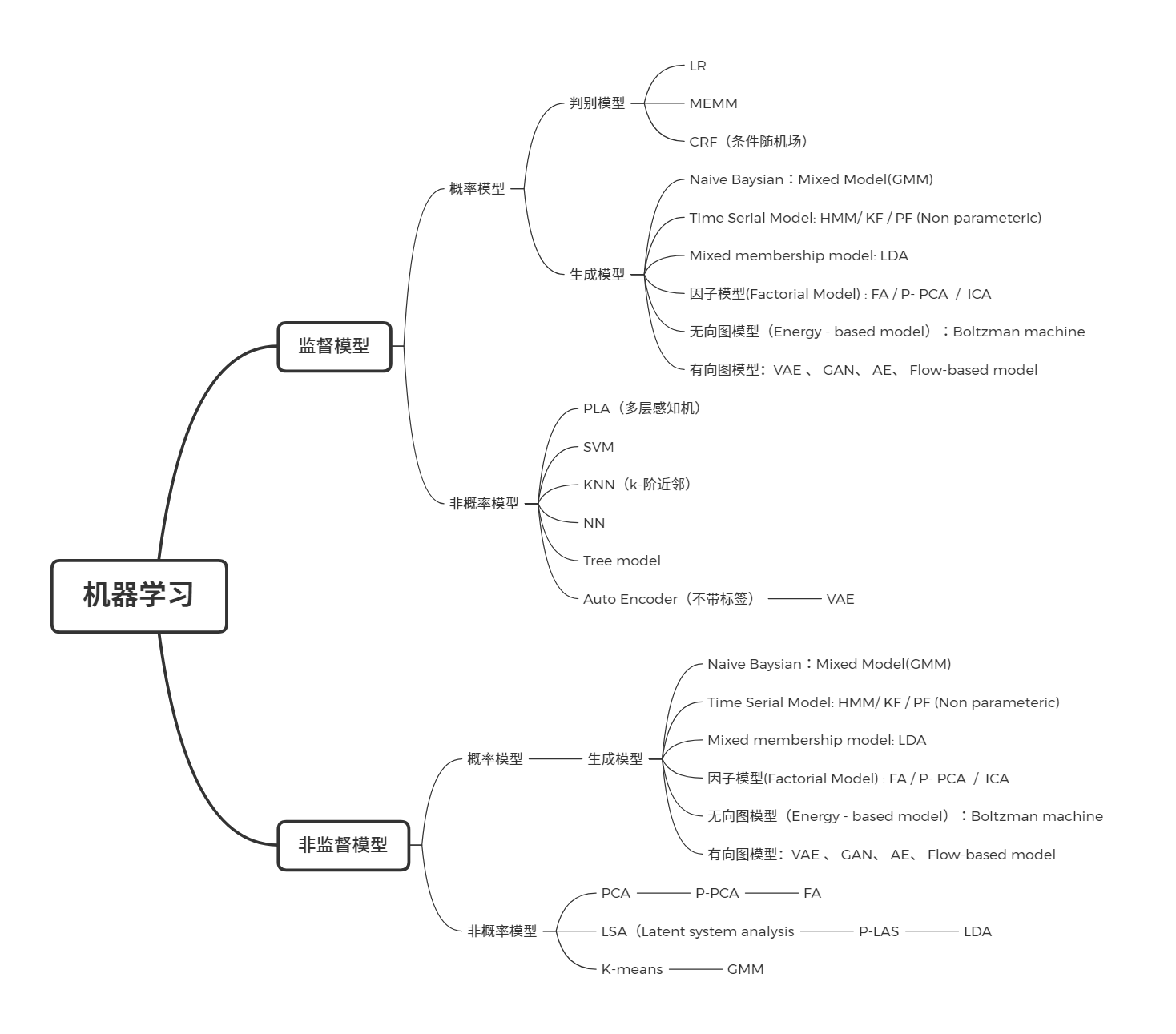
深度学习--GAN学习笔记

生成模型

什么是生成模型？

GMM: 用来做聚类，（非监督学习）
NB（朴素贝叶斯）：（监督学习，可以用来做垃圾邮件分类）
Logistics 回归是生成模型吗？No！

生成模型与解决的任务之间没有必然的联系，关注的是样本本身。对于监督学习$p(x， y)$ , 非监督学习 $p(x,z)$ ，有些模型甚至仅用 $X$ , 成为 Autoregression model 。

GAN(生成式对抗网络)

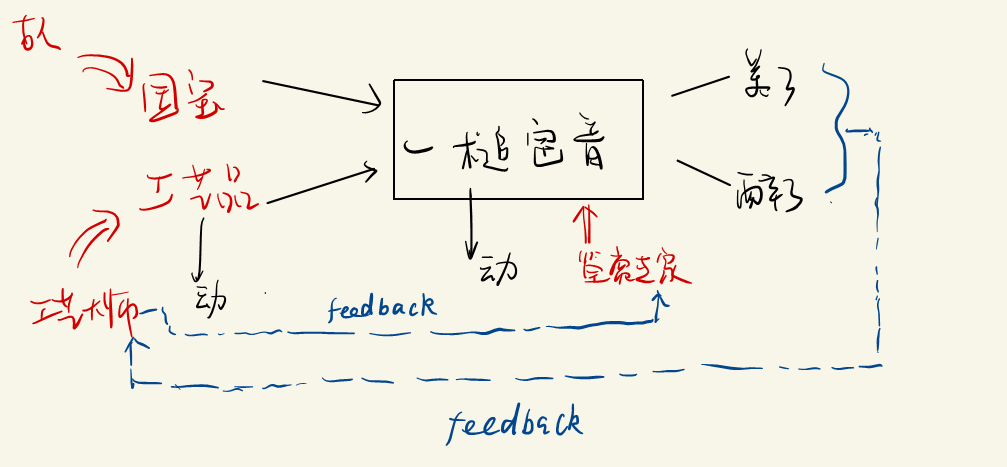
工艺大师的目的：成为高水平，可以以假乱真的大师。($P_g \rightarrow P_d $)

如果用统计模型去刻画这个模型，如何去表示？模型中的生成器和判别器可以通过一些模型去表示。

GAN的流程：

Initialize the generator and dicriminator
In each traning iteration
- Step 1 : Fixed generator G , and update discriminator D.
- Step 2 : Fixed Discriminator D , and update generator G ;

Auto - Encoder

graph LR
A[Random Generator] -->C(N.N)
F(A vector as code) --> C(N.N Decoder)
C --> D[N.N Decoder] -->G[Image]

VAE

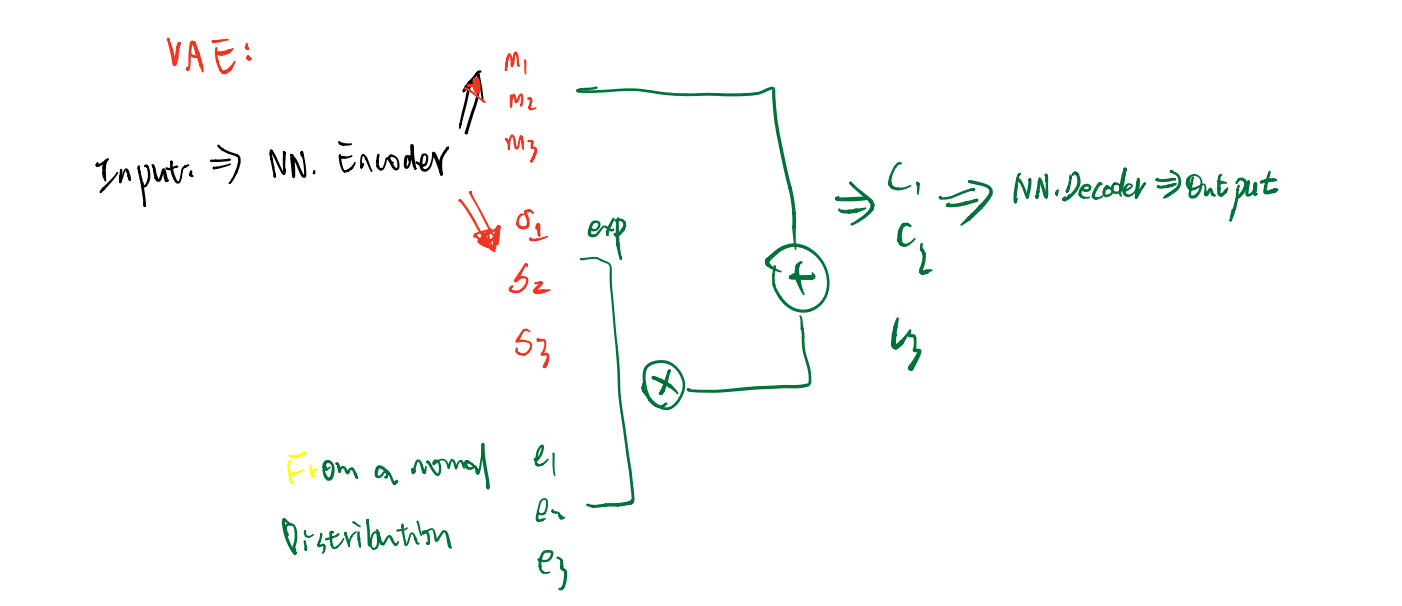
这里会对 $\sigma$ 进行限制：

\[\min ~ \sum_{i} ^{3} \left[ exp(\sigma_{i}) - (1+\sigma_{i}) + m_{i}^{2} \right]
\]

VAE存在着一些问题：它不能真的尝试去模拟真的图像

GAN——数学表示

数学符号：

$\{x_{i}\}_{i}^{N}$ 样本数据
$P_{data}：$ Population Density
$P_g(x;\theta_{g}):$ 生成模型的density；可以用 NN 进行逼近
$z \sim P_{Z}(Z)$ , Proposed Density，一般用来生成 $\tilde{x}_{i}$
$D(Z) = D(\tilde{x},\theta_{d}):$ 表示 Discrimination 识别是否是“国宝”的概率，越接近于1，越可能是国宝
$\tilde{x} = G(z;\theta_g)$

graph LR
A[Z] -->B(N.N)
B --> C{N.N}
F(P_data) --> C{N.N}
C -->|YES| D[国宝]
C -->|NO| E[赝品]

G[Z]-->H(N.N)-->I(tilde_x)

对于高专家来说：

如果 $x$ 是来自于 $P_{data}$ , 我们可以发现 $D(x;\theta_{d})$是较大的 $\Longrightarrow$ $\log(D(x;\theta_{d}))$ 是较大点的；
如果 $x$ 是来自于 $P_{generator}$ , 我们可以发现 $D(x;\theta_{d})$是较小的 $\Longrightarrow$ $1 - D(x;\theta_{d})$是较大点的$\Longrightarrow$ $\log(1 -D(G(Z))$是较大的；

所以对于高专家的目标函数为：

\[\max_{D} \rm E_{x \sim P_{data}} [~\log P(x)~] + E_{z \sim P_{z}} [~ \log (1 - D(Z))~]
\]

对于高级技师来说，想以假乱真：

如果 $x$ 是来自于 $P_{generative}$ , 我们可以高级技师希望 $D(x;\theta_{d})$是较大的 $\Longrightarrow$ $\log(1 -D(G(Z))$是较小的；

\[\min_{G}~ \rm E_{Z \sim P_{Z}} [~ \log( 1- D[G(Z)]) ]
\]

所以在这个体系中，总的目标为：

\[\min_{G} \max_{D} ~ \rm E_{x \sim P_{data}} [~\log P(x)~] + E_{z \sim P_{z}} [~ \log (1 - D(Z))~]
\]

小结：GAN的复杂度在于模型的学习，我们并没有直接面对$P_g (x , \theta_{g})$ ，而是用神经网络去逼近$P_g (x , \theta_{g})$ ,所以GAN是一种 Implict Density Model 。

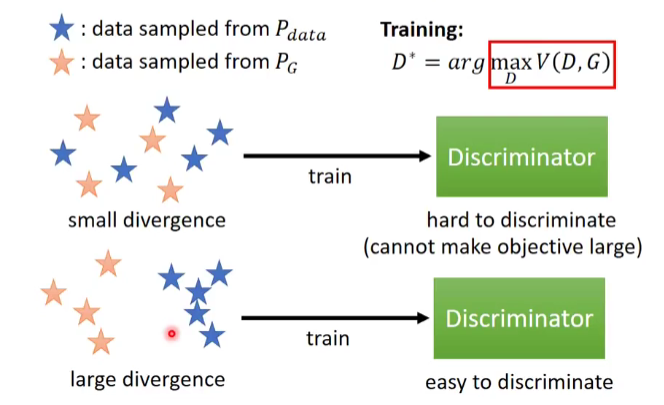
GAN存在最优解吗？

一般来说，我们会从MLE (Maximum Likelihood Estimation) 角度去解目标函数，但在GAN模型中，我们可以不通过MLE，而通过神经网站逼近Prob Density。

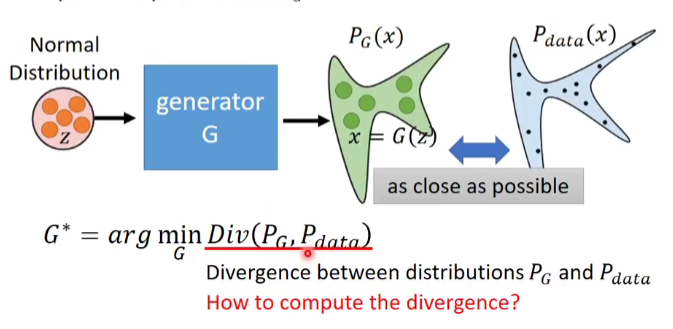
f-divergence

Definition: P and Q are two distribution . $p(x)$ and $q(x)$ are the probability of sampling of sampling x.

\[D_{f}(P||Q) = \int_{x} q(x)f\left( \frac{p(x)}{q(x)}\right) dx
\]

Remark : $f$ function is convex , $f(1) = 0$ , $D_{f}({P||Q})$ evaluates the differences of P and Q.

if $p(x)$ = $q(x)$ for all $x$, $D_{f}({P||Q}) = 0$ ; if $p(x) = q(x)$ for some $x$ ,
\[D_{f}({P||Q})= \int_{x} q(x) f \left( \frac{p(x)}{q(x)}\right) dx \geq f \left[ \int_{x} q(x) \cdot \frac{p(x)}{q(x)} dx \right] = 0
\]

Fenchel Congjugate

every conex function $f$ have a Congjugate function $f^{*}$；$f^{*}$ also is a convex function . We can find that $(f^{*})^{*} = f$

\[f^{*}(t) = \max_{x \in dom (f)} {xt - f(x)} \Longleftrightarrow
f (x) = \max_{t \in dom (f^{*})} {xt - f^{*}(t)}
\]

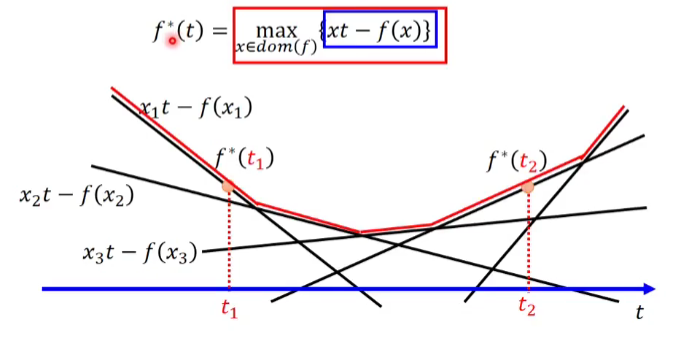
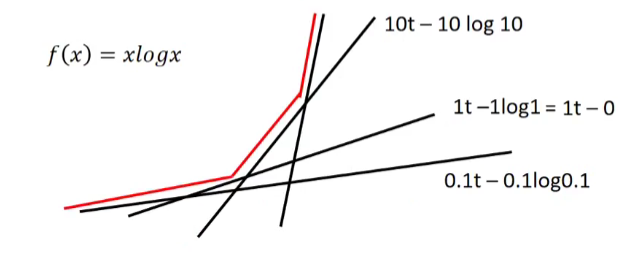
if $f(x) = x \log x$ , $f^{*}(t) = e^{t-1}$

\[\begin{aligned}
D_{f}(P||Q) & = \int_{x} q(x)f\left( \frac{p(x)}{q(x)}\right) dx \\
& = \int_{x} q(x) \left[ \max_{t \in dom(f)}
\left( \frac{p(x)}{q(x)} t - f^{*} (t) \right) \right]dx \\
& \approx \max_{D} \int_{x} p(x)D(x)dx - q(x)f^{*}\left(D(x) \right) dx
\end{aligned}
\]

Where $t = D(x)$ ; D is a function , whose input is $x$ , Output is $t$

\[\begin{aligned}
D_{f}(P||Q) & \ge \int_{x} q(x) \left[
\left( \frac{p(x)}{q(x)} D(x) - f^{*} \left(D(x) \right) \right) \right]dx \\
& = \int_{x} p(x)D(x)dx - q(x)f^{*}\left(D(x) \right) dx
\end{aligned}
\]

GAN角度

这里出现了一个问题，我们并不知道 $P_{g}$ 和 $P_d$ 这两个分布，怎么去求解？在GAN角度中,我们可以通过从 $p_{g}$ 和 $p_d$ 中抽样的方法去求解生成器。

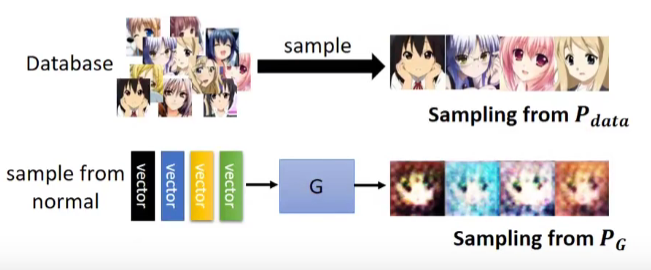
站在GAN的角度如何测量KL Div

GAN是从对抗学习的角度，因此我们要思考最优解存在吗？如果存在，$P_{g} \stackrel{？}{=} P_{d a t a}$

我们引用论文中的符号：

\[V(G,D) \equiv \rm E_{x \sim p(x)} \left[ \log (x)\right]
+ E_{x \sim p_{g}} \left[ \log \left( 1 - D\left(X \right )\right) \right]
\]

因此我们的目标函数可以写为：

\[\min_{G} \max_{D}~ V(G,D)
\]

Asumption:

$G(x)$ can be any fuction

求解步骤：

Step 1 : Given G , what is optimal $D^{*}$ maximizing

\[\begin{aligned}
\max_{D} ~ V(D,G) & = \int p_{data} \log \left(D\left(x \right)\right) dx +
\int p_{g} \log \left[ \left( 1- D(x) \right) \right] dx \\
& = \int \left[ p_{data} \log D(x) + p_{g} \log(1-D(x)) \right] dx
\end{aligned}
\]

FOC Condition：

\[\begin{aligned}
\frac{\partial} {\partial D} V(D,G) & = \frac{\partial }{\partial D}
\left [ \int \left[ p_{data} \log D + p_{g} \log(1-D(x)) \right] dx \right] \\
& = \int \frac{\partial }{\partial D}\left[ p_{data} \log D + p_{g} \log(1-D(x)) \right] dx \\
& = \int \left[ p_{data} \frac{1}{D(x)} + p_{g}
\frac{-1}{1-D(x)}\right] D^{\prime}(x)~ dx \stackrel{\Delta}{=}
0
\end{aligned}
\]

Remark: 这里定积分和求导可以互换顺序，$D(x) \in [0,1]$, 从FOC条件可以得到：

\[p_{d} \frac{1}{D(x)} = p_{g} \frac{1}{1-D(x)} ~ \Longrightarrow ~ p_d [1-D(x)] = p_{g}D(x)
~ \Longrightarrow ~ D^{*} (x) = \frac{p_{d}}{p_{d} + p_{g}}
\]

Step 2: 把 $D^{*}$ 带入目标函数，则有：

\[\begin{aligned}
\min_{G} \max_{D} V (G,D) & = \min_{G} V (G, D^{*}) \\
& = \min_{G} \rm E_{x \sim p_{d}} \log \left[
\frac{p_{d}}{p_{d} + p _{g}}\right]
+ E_{x \sim p_{g}} \log \left[ \frac{p_{g}}{p_{d}+p_{g}}\right]
\end{aligned}
\]

这个表达式与 KL Divergence 的形式非常像，可以用 KL来表示吗？p 或 q 为一个Prob Density 。

\[KL(p || q) = \rm E_{p} \left[ \log \frac{p}{q}\right] \ge 0
\]

答案是可以的，需要一些小技巧， $ 0 \le JSD < \le 2$ .

\[\begin{aligned}
\min_{G} \max_{D} V(G, D) & = \min_{G} \rm E_{x \sim p_{d}} \log \left[
\frac{p_{d}}{p_{d} + p _{G}}\right]
+ E_{x \sim p_{G}} \log \left[ \frac{p_{g}}{p_{d}+p_{G}}\right] \\
& = \min_{G} \rm E_{x \sim p_{d}} \log \left[
\frac{p_{d}}{\left( p_{d} + p _{G} \right) \2} \frac{1}{2} \right]
+ E_{x \sim p_{G}} \log \left[ \frac{p_{G}}{ \left (p_{d}+p_{G}\right) \2}
\frac{1}{2} \right] \\
& = \min_{G} KL[~ p_d || \frac{p_{d} + p_{G}}{2}~] +
KL[~p_g || \frac{p_{d} + p_{G}}{2}~] - \log(4) \\
& = 2JSD(P_{data} ||p_{G} ) - \log4
\end{aligned}
\]

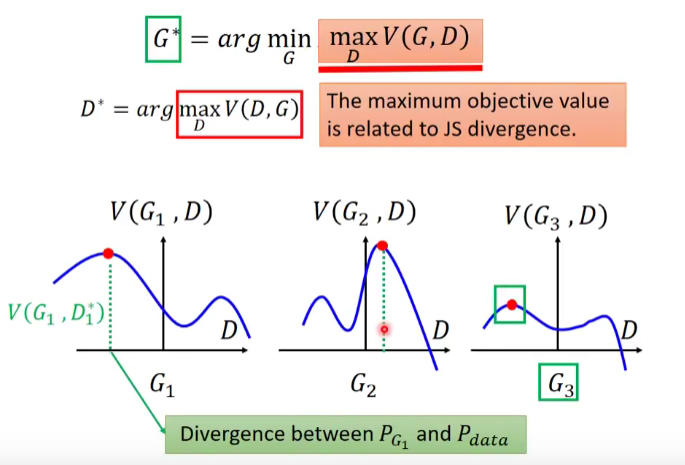
什么时候等式成立？当且仅当 $p_{d} = p_{G} = \frac{p_d + p_{G} }{2}$ , 可以解出 $p_{d}^{*} = p_{G }^{*}$ = 0.5 , $G^{*} = 0.5$，这意味着什么？在最有的情况下，复制出来的工艺品，送给 Discriminator 已经无法识别真假。

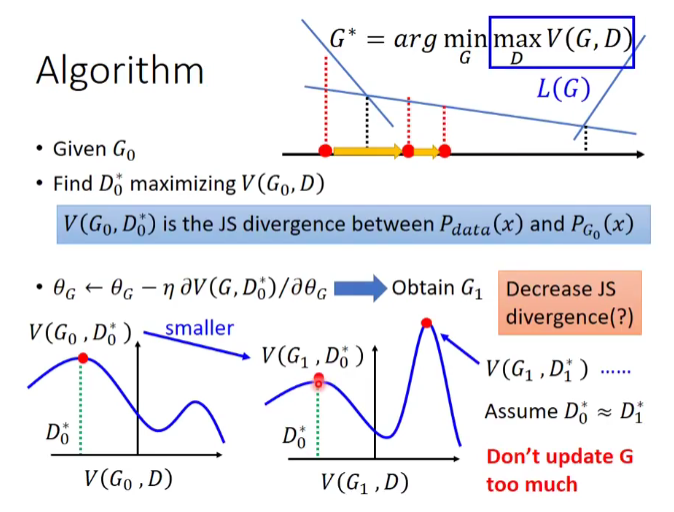
Algorithm:

Given $G_{0}$
Find $D_{0}^{*}$ maxmizing $V(G_{0}, D)$
$\theta_{G} \leftarrow \eta ~ \partial V(D,G_{0}^{*}) / \partial \theta_{G} $ $\Longrightarrow$ obtain $G_{1}$

$V(G_{0}, D_{0}^{*})$ is the JS Divergence between $p_{data}(x)$ and $p_{G_{0}}$

Find $D_{1}^{*}$ maxmizing $V(G_{1}, D)$
\[\theta_{G} \leftarrow \eta ~ \partial V(D,G_{1}^{*}) / \partial \theta_{G} $$ obtain $G_{2}$

\]
......

In Practice

Given G , How to compute $\max V(G, D)$
- sample {$x^{1}, x^{2}, \ldots ,x^{m}$} from $p_{data}(x)$ , sample {$\tilde{x}^{1}, \tilde{x}^{2}, \ldots ,\tilde{x}^{m}$} from $p_{G}(x)$
  \[\max V = \frac{1}{m} \sum_{i}^{m} \log D(x^{i}) +
  \frac{1}{m} \sum_{i}^{m} \left[\log 1 - D( \tilde{x}^{i}) \right]
  \]
Remark： In binary classifier , D is the binary classifier with the sigmoid output . {$x^{1}, x^{2}, \ldots ,x^{m}$} from $p_{data}(x)$ can be viewed as positive examples , {$\tilde{x}^{1}, \tilde{x}^{2}, \ldots ,\tilde{x}^{m}$} from $p_{G}(x)$ can be viewed as negative examples. Our goal is to minimize the cross-entropy. this is equal to the $\max V$

Summary

Algorithm:

initialize $\theta_{d}$ for $D$ and $\theta_{g}$ for $G$
In each training iterations (k times) :
- sample m {$x^{1}, x^{2}, \ldots ,x^{m}$} from data distribution $p_{data}(x)$
- sample m noize {$z^{1}, z^{2}, \ldots ,z^{m}$} from prior distribution $p_{prior}(z)$
- obaining the generated data {$\tilde{x}^{1}, \tilde{x}^{2}, \ldots ,\tilde{x}^{m}$} , $\tilde{x}^{i} = G(z^{i})$
- update discriminator parameters $\theta_{d}$ to maxmize
  - $\max \tilde{V} = \frac{1}{m} \sum_{i}^{m} \log D(x^{i}) +
    \frac{1}{m} \sum_{i}^{m} \left[\log 1 - D( \tilde{x}^{i}) \right]$
  - $\theta_{d} \leftarrow \eta ~ \Delta \tilde{V}(\theta_{d})$
以上是测量 JSD，下面是最小化 JSD , 即 Learning Genarator , 但是不能 train 太多次。
- sample another m noise samples {$z^{1}, z^{2}, \ldots ,z^{m}$} from prior distribution $p_{prior}(z)$
- update discriminator parameters $\theta_{g}$ to minmize
  - $\min \tilde{V} = \frac{1}{m} \sum_{i}^{m} \log D(x^{i}) +
    \frac{1}{m} \sum_{i}^{m} \left[\log 1 - D \left(G \left( z^{i}\right) \right) \right]$
  - $\theta_{g} \leftarrow \eta ~ \Delta \tilde{V}(\theta_{g})$

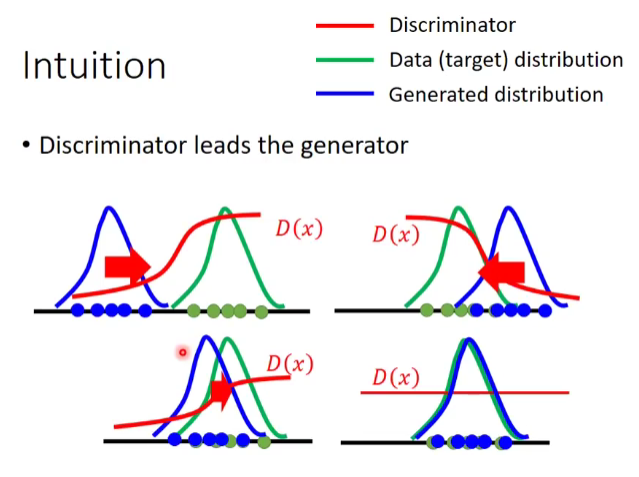
Intution

W - GAN

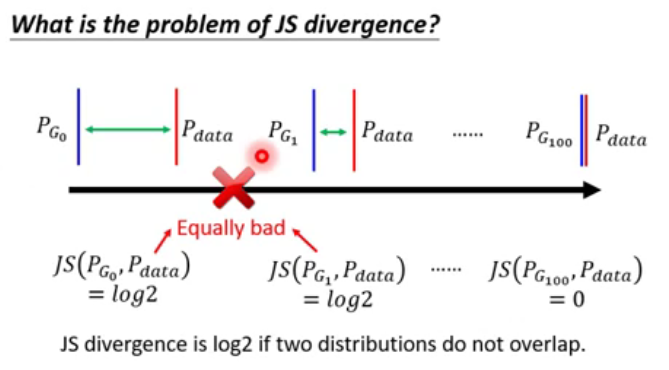
WGAN

Considering one distribution P as a pile of earth , and another distribution Q as a target . The average distance the earther mover has to move the earth .

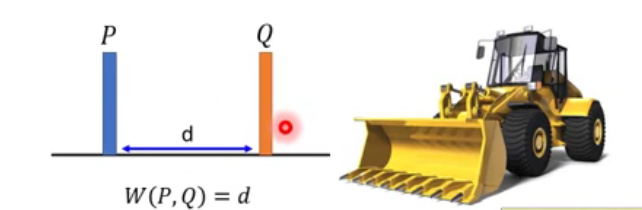
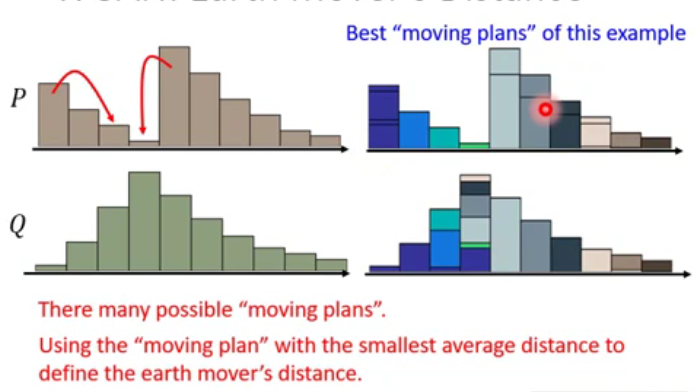
What's the moving plan ?

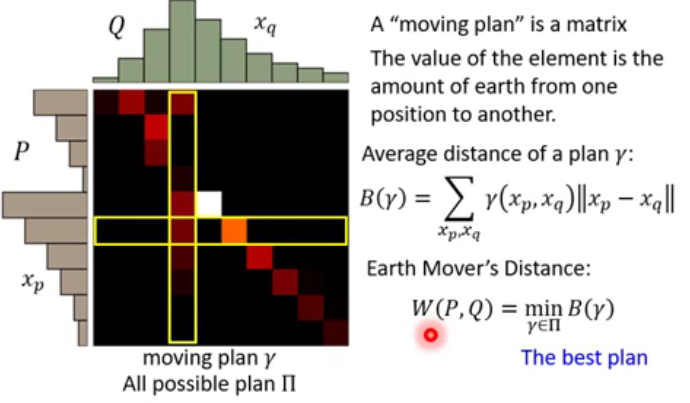
A "Moving plan " is matrix, the values of the element is the amount of earth from one position to another.

Average distance of a plan $\gamma$ :

\[B(\gamma) = \sum_{x_{p}, x_{q}} \gamma(x_{p}, x_{q})||x_{p} - x_{q} ||
\]

Earth Distance:

\[W(P, Q) = \min_{\gamma \in \prod } B(\gamma)
\]

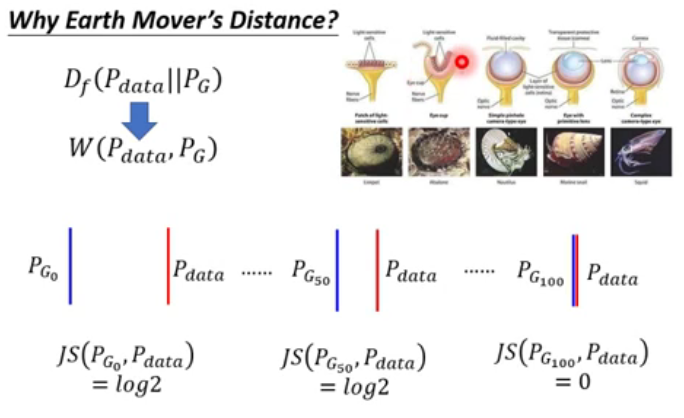
Evaluate the wasserstein distance between $p_{data}$ and $p_{g}$; D has to be smooth enough .

\[ V(G,D) = \max_{D \in 1-Lipschitz } \{ E_{x \sim p_{data}}[D(x)] + E_{x \sim p_{G}} [D(x)]\}
\]

Without the constraint , the trainning of D will not converge.
Keep the D smmoth forces $D(x)$ become $\infin$ to $-\infin$
What's the Lipschitz ?

\[k - Lipschitz ~~ function: ~~||f(x_{1}) - f(x_{2}) \le k ||x_{1}-x_{2}||
\]

How to Solve ?

Weight Clipping : Force the parameters w between c and -c , After parameter update , if $w > c$ ，$w = c$; if $w < - c$ ,$w = -c$