信号处理——傅里叶变换(FT-DTFT-DFT)

作者：桂。

时间：2017-01-17  23:41:13

链接：http://www.cnblogs.com/xingshansi/articles/6294111.html

声明：转载请注明出处，谢谢。

---

前言

信号处理一个重要的关系就是时域与频域的关系，本专题为：信号处理的频域处理。

本文主要讲述信号从时域连续信号到数字信号的变化，以及对应的频域关系，内容较为基础，公式不作具体推导。

理论分析

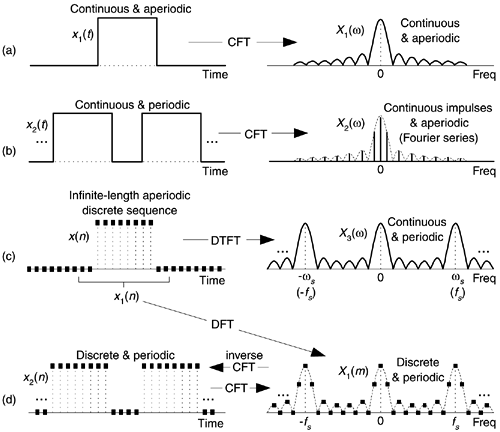
（图1 信号的时频对应关系）

　　A.傅里叶变换（FFT）

由图1（a）可以看出，连续非周期时域连续信号，对应频域信号仍然是连续信号。

对应的变换关系为：

时域——>频域

$F(\omega) = \int^{+\infty}_{-\infty} f(t) e^{-j\omega t}dt$

频域——>频域

$f(t) = \frac{1}{2\pi}\int^{+\infty}_{-\infty} F(\omega) e^{j\omega t}dt$

图1（b）为傅里叶级数，此处不作描述。

　　B.离散时间傅里叶变换(DTFT)

图1（c）表示对图1（a）在时域上进行采样，得到时域的离散信号，对应的频域信号仍然是连续信号，并且是以采样率为周期的周期信号。

对应的变换关系为：

时域——>频域

$F(e^{j\omega}) = \sum^{+\infty}_{-\infty} f(n) e^{-j\omega n}$

频域——>时域

$f(n) =\frac{1}{2\pi} \sum^{+\pi}_{-\pi} F(e^{j\omega}) e^{j\omega n}$

　　C.离散傅里叶变换（FFT）

图1（d）表述对图1（c）在频域上进行采样，得到的时域离散信号，对应的频域也变为离散信号。

对应的变换关系为：

时域——>频域

$F(k) = \sum^{N-1}_{n=0} f(n) e^{\frac{-j2\pi kn}{N}}$

频域——>时域

$f(n) = \frac{1}{N}\sum^{N-1}_{k=0} F(k) e^{\frac{j2\pi kn}{N}}$

三种变换的关系总结一下，关系如图2所示。至于FFT，是DFT的蝶形运算，本质相同，仅仅是运算不同，这里只是分析信号变换的对应关系，FFT的原理不作讨论。

（图2 三种变换的对应关系）