GSS3 C - Can you answer these queries III

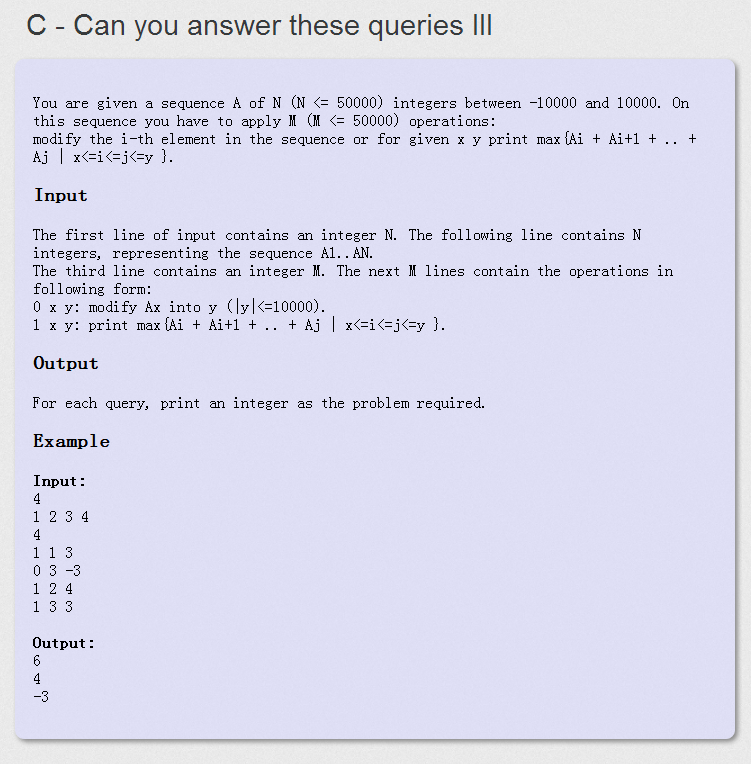
//在gss1的基础上加了修改操作，一样的做法，加一个modify函数就可以了
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;

const int N=5e4+;

int n,m,type,l,r;
int L,R,M,S;
struct Tree
{
    int l,r,mid;
    int sum,lmaxn,rmaxn,maxn;
}tree[N<<];

int read()
{
    char c=getchar();int num=,f=;
    for(;!isdigit(c);c=getchar())
        if(c=='-')
            f=-;
    for(;isdigit(c);c=getchar())
        num=num*+c-'';
    return num*f;
}

void pushup(int root)
{
    tree[root].maxn=max(tree[root<<].maxn,max(tree[root<<|].maxn,tree[root<<].rmaxn+tree[root<<|].lmaxn));
    tree[root].lmaxn=max(tree[root<<].lmaxn,tree[root<<].sum+tree[root<<|].lmaxn);
    tree[root].rmaxn=max(tree[root<<|].rmaxn,tree[root<<|].sum+tree[root<<].rmaxn);
    tree[root].sum=tree[root<<].sum+tree[root<<|].sum;
}

void build(int root,int l,int r)
{
    tree[root].l=l,tree[root].r=r,tree[root].mid=l+r>>;
    if(l==r)
    {
        tree[root].sum=tree[root].maxn=tree[root].rmaxn=tree[root].lmaxn=read();
        return;
    }
    build(root<<,l,tree[root].mid);
    build(root<<|,tree[root].mid+,r);
    pushup(root);
}

void Modify(int root,int pos,int x)
{
    if(tree[root].l==tree[root].r&&tree[root].l==pos)
    {
        tree[root].lmaxn=tree[root].rmaxn=tree[root].maxn=tree[root].sum=x;
        return;
    }
    if(pos<=tree[root].mid)
        Modify(root<<,pos,x);
    else
        Modify(root<<|,pos,x);
    pushup(root);
}

void Qeuery(int root,int l,int r,int &L,int &R,int &M,int &S)
{
    if(l<=tree[root].l&&tree[root].r<=r)
    {
        L=tree[root].lmaxn,
        R=tree[root].rmaxn,
        M=tree[root].maxn,
        S=tree[root].sum;
        return;
    }
    if(tree[root].mid>=r)
    {
        Qeuery(root<<,l,r,L,R,M,S);
    }
    else if(tree[root].mid<l)
    {
        Qeuery(root<<|,l,r,L,R,M,S);
    }
    else
    {
        int lL=,lR=,lM=,lS=,rL=,rR=,rM=,rS=;
        Qeuery(root<<,l,tree[root].mid,lL,lR,lM,lS);
        Qeuery(root<<|,tree[root].mid+,r,rL,rR,rM,rS);
        L=max(lL,lS+rL);
        R=max(rR,rS+lR);
        M=max(lR+rL,max(lM,rM));
        S=lS+rS;
    }
}

int main()
{
    n=read();
    build(,,n);
    m=read();
    for(int i=;i<=m;++i)
    {
        type=read();
        l=read(),r=read();
        if(!type)
            Modify(,l,r);
        else
        {
            Qeuery(,l,r,L,R,M,S);
            printf("%d\n",M);
        }
    }
    return ;
}