【组合数学】【P5520】[yLOI2019] 青原樱

A [yLOI2019] 青原樱

Background

星川之下皆萤火尘埃

我独行在人潮你天真而待

相遇若是借丹青着色

青原上 绯樱如海

——银临《青原樱》(Cover 人衣大人)

Description

给定 \(n\) 个位置，要求放下 \(m\) 个互不相同的东西，东西两两之间不能相邻，求方案数对 \(p\) 取模的结果。

Limitations

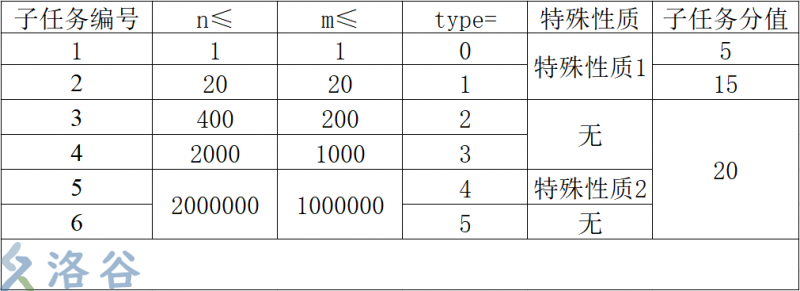
特殊性质1：保证对应测试点的实际方案数(在取模前)不超过 \(10^6\)

特殊性质2：保证 \(p\) 是一个质数。

对于 \(100\%\) 的数据，保证 \(1 \leq p \leq 10^9\)，\(1 \leq m \leq \lceil \frac{n}{2} \rceil\)

Solution

子任务 \(1\)：

显然 \(n = m = 1\)，所以共有 \(1\) 种方案，但是直接输出 \(1\) 是没有分的，因为这个点的 \(p = 1\)，应该输出 \(1 \bmod 1 = 0\)。

期望得分 \(5~pts\)

子任务 \(2\)：

考虑方案数不超过 \(10^6\)，因此只要在爆搜的时候保证搜索树上每个节点的情况都是合法的且他的后代一定至少存在一种合法的方案即可。考虑搜索树的最后一层节点数是 \(O(ans)\) 的，树共有 \(O(n)\) 层，因此总复杂度 \(O(n \times ans)\)，期望得分 \(15~pts\)

子任务 \(3\)：

数数题，考虑DP。

先不考虑幼苗的编号，设 \(f_{i, j}\) 为放了 \(i\) 个幼苗，第 \(i\) 个幼苗在位置 \(j\) 的方案数，转移显然：

\[f_{i, j} = \sum_{k = 0}^{j - 1}f_{i - 1,k}\]

初始化为 \(f_{0, 0} = 1\)。注意由于这里幼苗是互不相同的，因此算出答案以后要乘上 \(m!\)。

共有 \(O(nm)\) 个状态，每次转移是 \(O(n)\) 的，总复杂度 \(O(n^2m)\)，期望得分 \(20~pts\)

子任务 \(4\)：

考虑上面的转移方程显然可以对每个 \(i\) 维护一个前缀和来让转移变成 \(O(1)\)，于是总复杂度 \(O(nm)\)，期望得分 \(20~pts\)

子任务 \(5\)：

DP看起来已经到了尽头，无论如何状态数都不可能低于 \(O(nm)\)，于是考虑组合数学。

考虑将所有的方案分为两类：对于所有的第 \(n\) 个位置没有树苗的方案，归为第一类方案，有树苗的方案归为第二类方案。显然这两类方案囊括了所有可能的情况且互不相同。

先考虑第一种情况，第 \(n\) 个位置没有树苗。那么对于所有的 \(m\) 个树苗，显然每个树苗后面都紧跟着一个空位，如果将每个树苗和他后面的紧跟着的空位看作一个物品，那么问题就变成了共有 \((n - m)\) 个位置，在这 \((n - m)\) 个位置种选择 \(m\) 个位置，放上 \(m\) 个物品，摆放方式没有限制，求方案数。根据排列数的定义，共有 \(C_{n - m}^m\) 种方式。注意到这样求出的方案是 \(m\) 个物品相同的方案，由于要求 \(m\) 个物品互不相同的方案，答案应该乘上 \(m!\)。于是这种情况的方案数是 \(m! \times C_{n - m}^m\)。

再考虑第二种情况，第 \(m\) 个位置有树苗，那么对于前面的 \((n - 1)\) 个树苗，每个树苗后面都紧跟着一个空位，同样的我们将树苗和空位捆绑在一起看，那么不考虑最后一个树苗，问题变为有 \([(n - 1) - (m - 1) = n - m]\) 个位置，在这些位置种选择 \((m - 1)\) 个，共有 \(C_{n - m}^{m - 1}\) 种方式。注意到最后一个树苗的选择一共有 \(m\) 种情况，所以在 \(m\) 个树苗相同时的方案数应是 \(m \times C_{n - m}^{m - 1}\)。对于前面 \((m - 1)\) 个物品，有 \((m - 1)!\) 种排列方式，因此这种情况的总方案数为 \(m!~\times~C_{n - m}^{m - 1}\)

由于保证了模数 \(p\) 是一个质数，因此 \(O(n)\) 处理逆元后 \(O(n)\) 计算即可。期望得分 \(20~pts\)

子任务 \(6\)：

如果你足够机智（划掉。如果你不像扶苏一样傻），你就可以发现第一种方案的方案数 \(m! \times C_{n - m}^m~=~A_{n - m}^m\)，第二种方案的方案数 \(m! \times C_{n - m}^{m - 1}~=~m \times A_{n - m}^{m - 1}\)。所以根本不需要处理逆元，直接做即可。

当然，由于代数恒等式 \(A_x^y + y \times A_x^{y - 1} = A_{x + 1}^y\)，可以直接求 \(A_{n - m + 1}^{m}\)，时间复杂度 \(O(n)\)，期望得分 \(20~pts\)。