Manytasking optimization MATP
Manytasking Jmetal代码反向解析1_MATP测试函数集
觉得有用的话,欢迎一起讨论相互学习~Follow Me
- 这是我在写Manytask optimization时的笔记,代码地址可以下载
打开文件夹如下目录,选择benchmark中的任意一个测试函数集,此时我们选择
MATP1
MATP1
package momfo.problems.benchmarks;
import java.io.IOException;
import momfo.core.Problem;
import momfo.core.ProblemSet;
import momfo.problems.base.*;
public class MATP1 {
public static ProblemSet getProblem() throws IOException {
int taskNumber=50;
ProblemSet problemSet = new ProblemSet(taskNumber);
for(int i=1;i<=taskNumber;i++)
problemSet.add(getT(i).get(0));
return problemSet;
}
public static ProblemSet getT(int taskID) throws IOException {
ProblemSet problemSet = new ProblemSet(1);
MMDTLZ prob = new MMDTLZ(2, 50, 1, -100,100);
prob.setGType("sphere");
double[][] matrix = IO.readMatrixFromFile("MData/M1/M1_"+taskID+".txt");
double shiftValues[] = IO.readShiftValuesFromFile("SVData/S1/S1_"+taskID+".txt");
prob.setRotationMatrix(matrix);
prob.setShiftValues(shiftValues);
((Problem)prob).setName("MATP1-"+taskID);
problemSet.add(prob);
return problemSet;
}
}
int taskNumber=50;表示MATP1问题设置的任务个数是50,初始化problemSet作为一个容器以承载每一个被初始化后的实际MATP1问题。for(int i=1;i<=taskNumber;i++) problemSet.add(getT(i).get(0));
意味着此时需要关注的是getT函数,从MMDTLZ prob = new MMDTLZ(2, 50, 1, -100,100); prob.setGType("sphere");看出MATP_1是一个双目标的问题,并且决策变量个数为50,决策变量最小值为-100,最大值为100,而G函数的类型为
sphere,而只要是双目标的函数使用的H函数都是circle
```java
// MMDTLZ
if (numberOfObjectives == 2)
hType_ = "circle";
else
hType_ = "sphere";
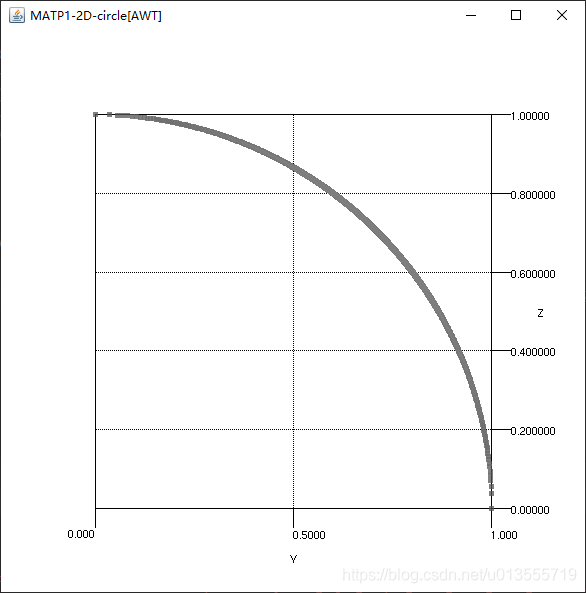
* **通过**double[][] matrix = IO.readMatrixFromFile("MData/M1/M1_"+taskID+".txt");
double shiftValues[] = IO.readShiftValuesFromFile("SVData/S1/S1_"+taskID+".txt");
``* 可知matrix[][]其中保存有旋转函数,根据taskID具有不同的旋转角度,shiftValues则保存了偏移向量,通过不同的旋转函数和偏移向量可以保证MATP问题中的不同任务即使具有相同的帕累托前沿,但是对应的决策变量距离和位置却完全不同。  ## 注意在MATP2中仅仅设置G函数的形状为sphere和alpha`值1。(后期通关观察得知,alpha值是用于计算cos函数的)
MATP2
public class MATP2 {
public static ProblemSet getProblem() throws IOException {
int taskNumber=50;
ProblemSet problemSet = new ProblemSet(taskNumber);
for(int i=1;i<=taskNumber;i++)
problemSet.add(getT(i).get(0));
return problemSet;
}
public static ProblemSet getT(int taskID) throws IOException {
ProblemSet problemSet = new ProblemSet(1);
MMZDT prob = new MMZDT(50, 1, -100,100);
prob.setGType("mean");
prob.setHType("concave");
double[][] matrix = IO.readMatrixFromFile("MData/M2/M2_"+taskID+".txt");
double shiftValues[] = IO.readShiftValuesFromFile("SVData/S2/S2_"+taskID+".txt");
prob.setRotationMatrix(matrix);
prob.setShiftValues(shiftValues);
((Problem)prob).setName("MATP2-"+taskID);
problemSet.add(prob);
return problemSet;
}
}和MATP1问题不同的是MATP2问题设置G函数为mean,设置H函数为concave,最终形状为concave并且是根据ZDT问题改编的,而不是DTLZ问题,表示有50个变量,并且K值为1,根据ZDT问题的默认函数来看,ZDT问题构造的都是双目标问题。
public MMZDT(int numberOfVariables, int k, double lg, double ug) {
numberOfObjectives_ = 2;
numberOfVariables_ = numberOfVariables;
k_ = k;
gType_ = "sphere";
f1Type_ = "linear";
hType_ = "convex";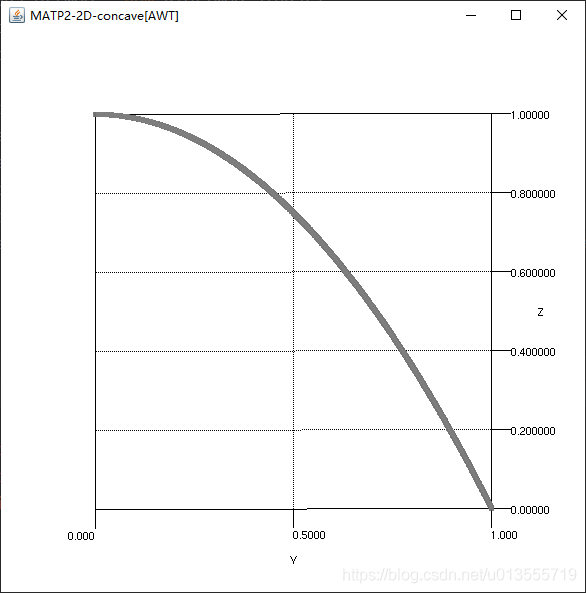
MATP3
package momfo.problems.benchmarks;
import java.io.IOException;
import momfo.core.Problem;
import momfo.core.ProblemSet;
import momfo.problems.base.*;
public class MATP3 {
public static ProblemSet getProblem() throws IOException {
int taskNumber=50;
ProblemSet problemSet = new ProblemSet(taskNumber);
for(int i=1;i<=taskNumber;i++)
problemSet.add(getT(i).get(0));
return problemSet;
}
public static ProblemSet getT(int taskID) throws IOException {
ProblemSet problemSet = new ProblemSet(1);
MMZDT prob = new MMZDT(10, 1, -5,5);
prob.setGType("rosenbrock");
prob.setHType("concave");
double[][] matrix = IO.readMatrixFromFile("MData/M3/M3_"+taskID+".txt");
double shiftValues[] = IO.readShiftValuesFromFile("SVData/S3/S3_"+taskID+".txt");
prob.setRotationMatrix(matrix);
prob.setShiftValues(shiftValues);
((Problem)prob).setName("MATP3-"+taskID);
problemSet.add(prob);
return problemSet;
}
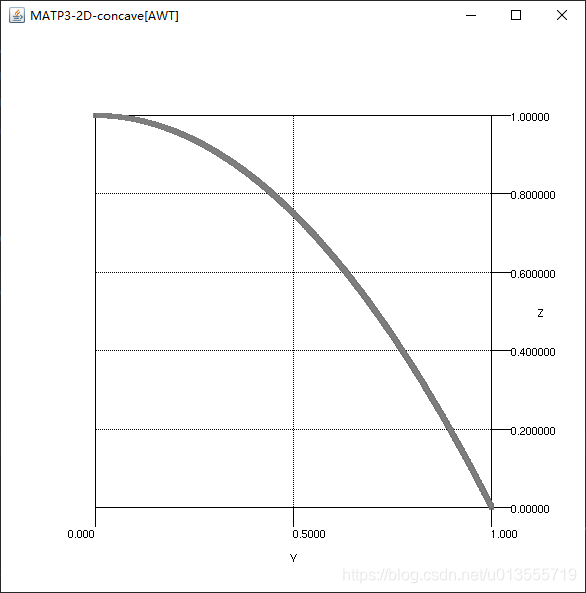
}和MATP1以及MATP2问题不同的是MATP3问题设置G函数为rosenbrock,设置H函数为concave,最终形状为concave并且是根据ZDT问题改编的,而不是DTLZ问题,表示有50个这样的任务,并且K值为1,根据ZDT问题的默认函数来看,ZDT问题构造的都是双目标问题,与MATP2问题不同的是使用10个变量,并且变量范围为[-5,5]而不是[-50,50]
MATP4
import java.io.IOException;
import momfo.core.Problem;
import momfo.core.ProblemSet;
import momfo.problems.base.*;
public class MATP4 {
public static ProblemSet getProblem() throws IOException {
int taskNumber=50;
ProblemSet problemSet = new ProblemSet(taskNumber);
for(int i=1;i<=taskNumber;i++)
problemSet.add(getT(i).get(0));
return problemSet;
}
public static ProblemSet getT(int taskID) throws IOException {
ProblemSet problemSet = new ProblemSet(1);
MMDTLZ prob = new MMDTLZ(2, 50, 1, -2,2);
prob.setGType("rastrigin");
double[][] matrix = IO.readMatrixFromFile("MData/M4/M4_"+taskID+".txt");
double shiftValues[] = IO.readShiftValuesFromFile("SVData/S4/S4_"+taskID+".txt");
prob.setRotationMatrix(matrix);
prob.setShiftValues(shiftValues);
((Problem)prob).setName("MATP4-"+taskID);
problemSet.add(prob);
return problemSet;
}
}
可以看出MATP4使用的是DTLZ函数其中具有两个目标函数,具有50个决策变量,alpha值为1,上界为2下界为-2.使用的G函数为rastrigin,使用的H函数为sphere
//MMDTLZ
if (numberOfObjectives == 2)
hType_ = "circle";
else
hType_ = "sphere";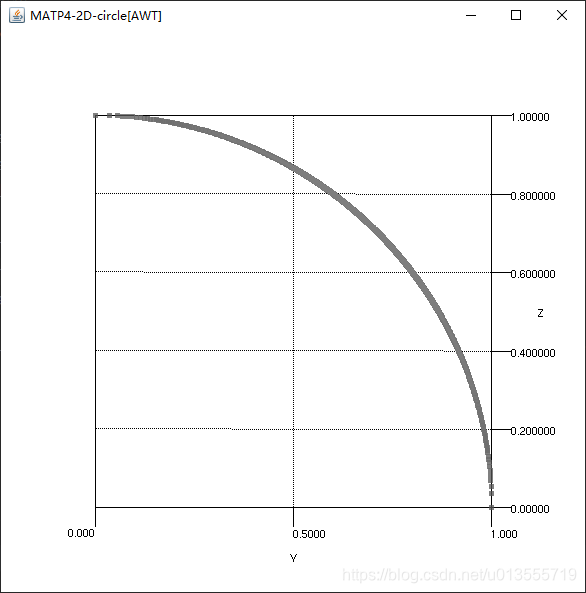
MATP5
package momfo.problems.benchmarks;
import java.io.IOException;
import momfo.core.Problem;
import momfo.core.ProblemSet;
import momfo.problems.base.*;
public class MATP5 {
public static ProblemSet getProblem() throws IOException {
int taskNumber=50;
ProblemSet problemSet = new ProblemSet(taskNumber);
for(int i=1;i<=taskNumber;i++)
problemSet.add(getT(i).get(0));
return problemSet;
}
public static ProblemSet getT(int taskID) throws IOException {
ProblemSet problemSet = new ProblemSet(1);
MMZDT prob = new MMZDT(50, 1, -1,1);
prob.setGType("ackley");
prob.setHType("convex");
double[][] matrix = IO.readMatrixFromFile("MData/M5/M5_"+taskID+".txt");
double shiftValues[] = IO.readShiftValuesFromFile("SVData/S5/S5_"+taskID+".txt");
prob.setRotationMatrix(matrix);
prob.setShiftValues(shiftValues);
((Problem)prob).setName("MATP5-"+taskID);
problemSet.add(prob);
return problemSet;
}
}
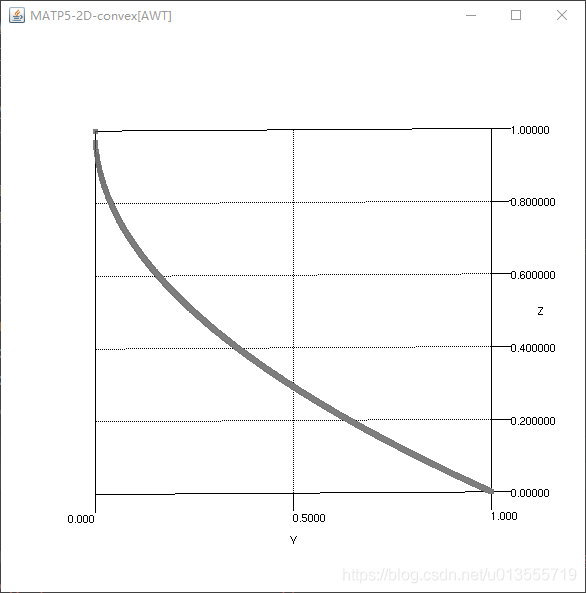
决策变量个数为50,k为1,变量最小范围为-1,变量最大范围为1,G函数为ackley,H函数为convex
MATP6
package momfo.problems.benchmarks;
import java.io.IOException;
import momfo.core.Problem;
import momfo.core.ProblemSet;
import momfo.problems.base.*;
public class MATP6 {
public static ProblemSet getProblem() throws IOException {
int taskNumber=50;
ProblemSet problemSet = new ProblemSet(taskNumber);
for(int i=1;i<=taskNumber;i++)
problemSet.add(getT(i).get(0));
return problemSet;
}
public static ProblemSet getT(int taskID) throws IOException {
ProblemSet problemSet = new ProblemSet(1);
MMDTLZ prob = new MMDTLZ(2, 50, 1, -50,50);
prob.setGType("griewank");
double[][] matrix = IO.readMatrixFromFile("MData/M6/M6_"+taskID+".txt");
double shiftValues[] = IO.readShiftValuesFromFile("SVData/S6/S6_"+taskID+".txt");
prob.setRotationMatrix(matrix);
prob.setShiftValues(shiftValues);
((Problem)prob).setName("MATP6-"+taskID);
problemSet.add(prob);
return problemSet;
}
}
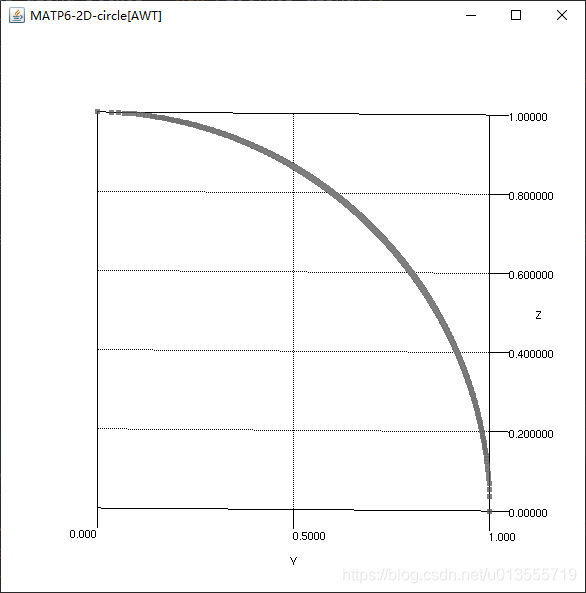
目标函数2个,50个决策变量,alpha值设置为1,下边界为-50,上边界为50,G函数为griewank,H函数为circle
MATP算例总结
float[] rgb1 = {0, 0, 0};//黑色-circle
float[] rgb2 = {(float) 0, (float) 0, (float) 139};//蓝黑-concave
float[] rgb3 = {(float) 255, (float) 0, (float) 0};//红色-concave
float[] rgb4 = {(float) 0, (float) 255, (float) 0};//绿色-circle
float[] rgb5 = {(float) 255, (float) 255, (float) 0};//黄色-convex
float[] rgb6 = {(float) 139, (float) 69, (float) 19};//巧克力色-circle
float alpha = (float) 1;
Scatter scatter1 = tools.Setpoint(TruePFT1_Matrix, rgb1, alpha, 20);
Scatter scatter2 = tools.Setpoint(TruePFT2_Matrix, rgb2, alpha, 15);
Scatter scatter3 = tools.Setpoint(TruePFT3_Matrix, rgb3, alpha, 8);
Scatter scatter4 = tools.Setpoint(TruePFT4_Matrix, rgb4, alpha, 10);
Scatter scatter5 = tools.Setpoint(TruePFT5_Matrix, rgb5, alpha, 6);
Scatter scatter6 = tools.Setpoint(TruePFT6_Matrix, rgb6, alpha, 5);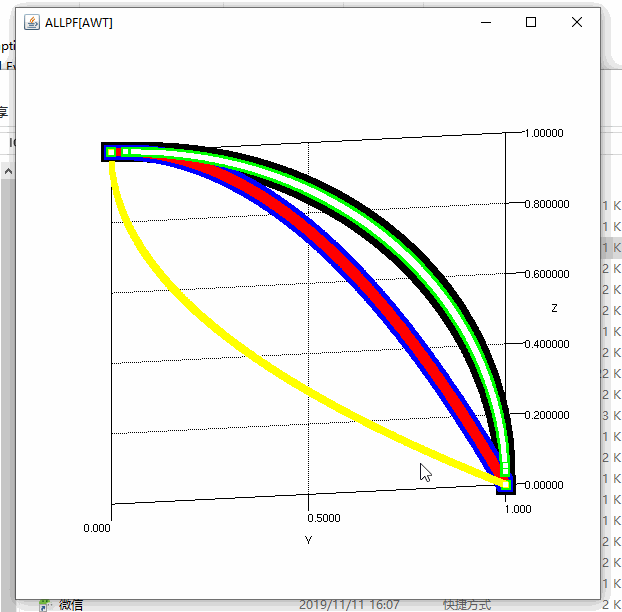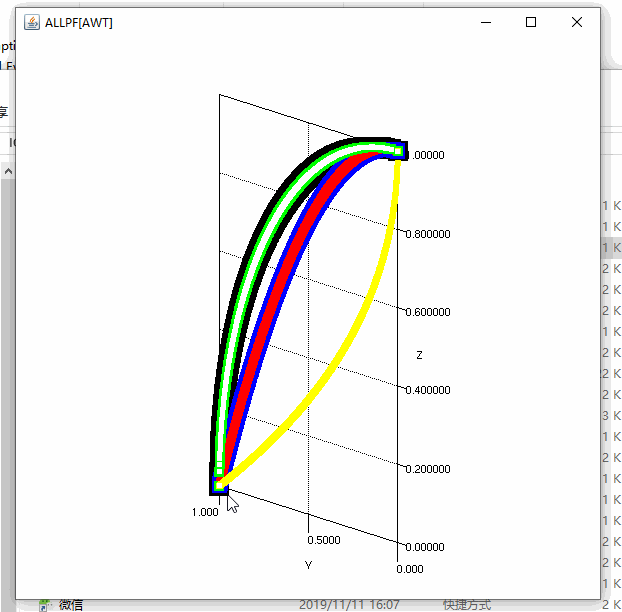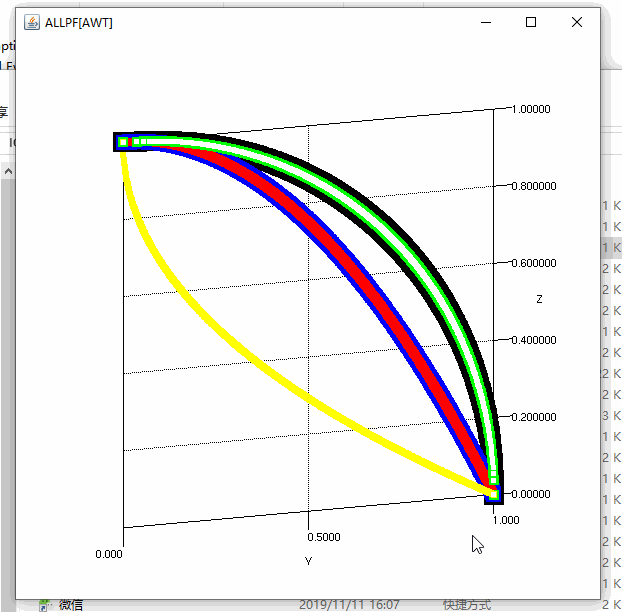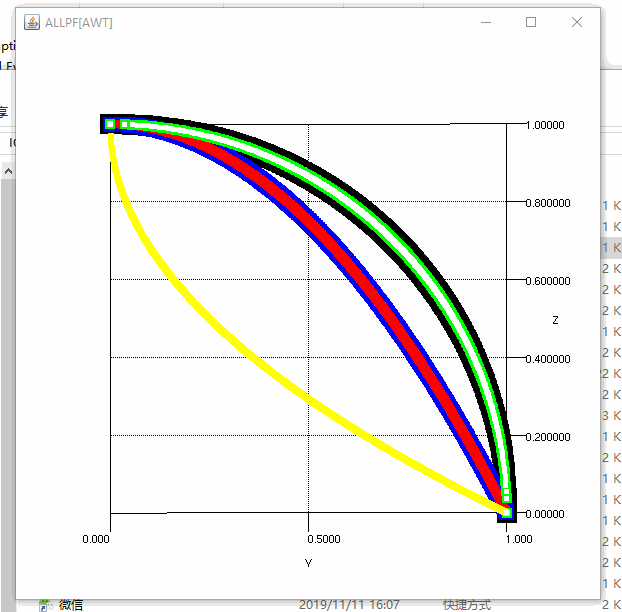
Manytasking optimization MATP的更多相关文章
- theano scan optimization
selected from Theano Doc Optimizing Scan performance Minimizing Scan Usage performan as much of the ...
- [Project Name] was compiled with optimization - stepping may behave oddly; variables may not be available.
控制台输出的时候显示一串这样的信息:[Project Name] was compiled with optimization - stepping may behave oddly; variabl ...
- Mvc 之System.Web.Optimization 压缩合并如何让*.min.js 脚本不再压缩
最近项目中用到了easy ui ,但是在配置BundleConfig 的时候出现了问题,easy ui的脚本jquery.easyui.min.js 压缩后出现各种脚本错误,总是莫名其妙的 i标量错误 ...
- MySQL Range Optimization
8.2.1.3 Range Optimization MYSQL的Range Optimization的目的还是尽可能的使用索引 The range access method uses a sing ...
- 命名空间“System.Web”中不存在类型或命名空间名称“Optimization”(是否缺少程序集引用?)
今天,在.net4.5,mvc4下新建了个区域,运行起来就报这个错误: 命名空间"System.Web"中不存在类型或命名空间名称"Optimization"( ...
- [阅读笔记]Software optimization resources
http://www.agner.org/optimize/#manuals 阅读笔记Optimizing software in C++ 7. The efficiency of differe ...
- Tomcat APR & Linux Optimization
一.简介 APR(Apache portable Run-time libraries)模式:简单理解,就是从操作系统级别解决异步IO问题,大幅度的提高服务器的处理和响应性能, 也是Tomcat运行高 ...
- low-rank 的相关求解方法 (CODE) Low-Rank Matrix Recovery and Completion via Convex Optimization
(CODE) Low-Rank Matrix Recovery and Completion via Convex Optimization 这个是来自http://blog.sina.com.cn/ ...
- hdu 1232, disjoint set, linked list vs. rooted tree, a minor but substantial optimization for path c 分类: hdoj 2015-07-16 17:13 116人阅读 评论(0) 收藏
three version are provided. disjoint set, linked list version with weighted-union heuristic, rooted ...
随机推荐
- 轻量级C#编辑器RoslynPad((基于Roslyn编译器))
简介 RoslynPad是一个Apache 2.0协议开源的轻量级C#编辑器.支持自动完成,语法提示,修改建议等功能.很适合平时随手写个C#程序看看运行结果. 目前版本:0.10.1,无需保存也可以运 ...
- 4484: [Jsoi2015]最小表示(拓扑序+bitset维护连通性)
4484: [Jsoi2015]最小表示 题目链接 题解: bitset的题感觉都好巧妙啊QAQ. 因为题目中给出的是一个DAG,如果\(u->v\)这条边可以删去,等价于还存在一个更长的路径可 ...
- eclipse解决中文字体太小问题(转载)
最近新装了Win7,打开eclipse3.7中文字体很小,简直难以辨认.在网上搜索发现这是由于Eclipse 3.7 用的字体是 Consolas,显示中文的时候默认太小了. 解决方式有两种:一. ...
- 用 gradle 运行 spring boot 项目
用 gradle 运行 spring boot 项目(网页中的第6章:https://docs.spring.io/spring-boot/docs/2.1.1.RELEASE/gradle-plug ...
- python的email、smtplib、poplib模块收发邮件
一封电子邮件的旅程是: MUA:Mail User Agent--邮件用户代理.(即类似Outlook的电子邮件软件) MTA:Mail Transfer Agent--邮件传输代理,就是那些Emai ...
- 16-Flutter移动电商实战-切换后页面状态的保持AutomaticKeepAliveClientMixin
底栏切换每次都重新请求是一件非常恶心的事,flutter 中提供了AutomaticKeepAliveClientMixin 帮我们完成页面状态保存效果. 1.AutomaticKeepAliveCl ...
- 未能找到 System.Web.Helpers
This question is a bit old but here's a simple solution - Microsoft seemed to just move this library ...
- MongoDB shell 2 副本集方法
rs.initiate() rs.addArb() rs.help() rs.printReplicationInfo() 查看到副本集操作日志 rs.remove() 减少副本集节点 r ...
- 文件搜索命令locate
与find命令不同,locate命令不会去搜索某一个分区或硬盘,而是直接在资料库中搜索,因此,搜索的速度要比find命令快得多,linux系统会定期更新资料库. 利用locate locate命令可以 ...
- P1005 矩阵取数
题目链接 看完题可能第一时间并没有清晰的思路.让我们一步一步的来考虑这道题目. 题目中描述操作为每次从所有的行中选取,这样做有些麻烦.仔细思考一下可以发现行与行之间互不干涉,所以我们可以对每行操作到底 ...
