BZOJ5415:[NOI2018]归程(可持久化并查集,最短路)

Description

Input

Output

Sample Input1

1
4 3
1 2 50 1
2 3 100 2
3 4 50 1
5 0 2
3 0
2 1
4 1
3 1
3 2

Sample Output1

0
50
200
50
150

Sample Input2

1
5 5
1 2 1 2
2 3 1 2
4 3 1 2
5 3 1 2
1 5 2 1
4 1 3
5 1
5 2
2 0
4 0

Sample Output2

0

2

3

1

HINT

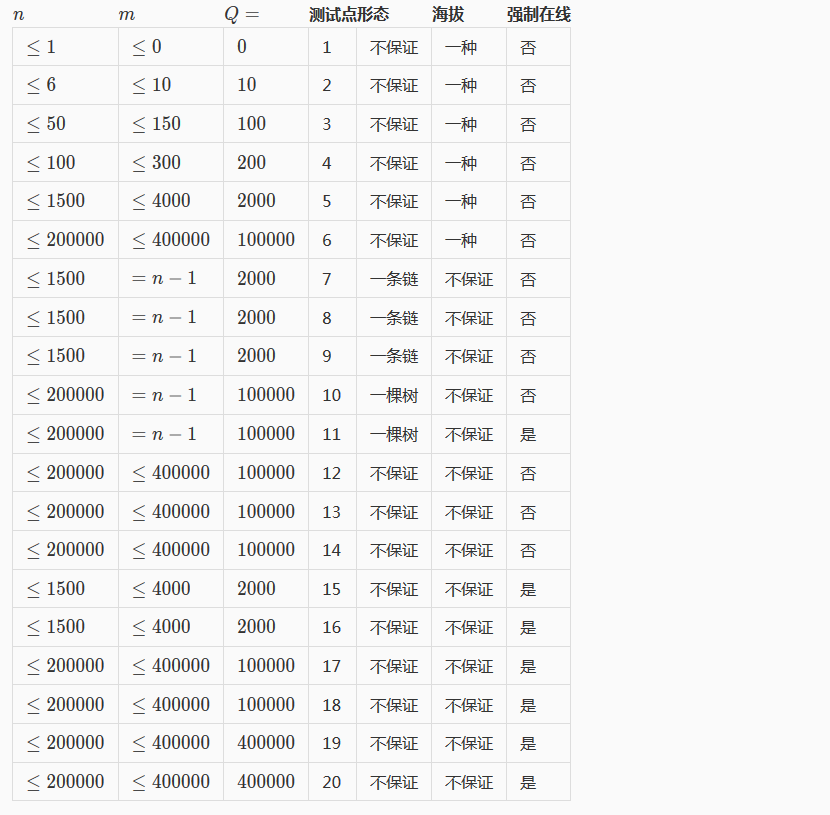
Solution

会了可持久化并查集这题可能会被卡的正解就很好写了……

把边按高度大小从大到小加入，用可持久化并查集记下每一个时刻并查集的联通情况，

同时用持久化的$Min[i]$数组记录$i$点所在的连通块内到点$1$的最近距离。查询的时候二分到对应时刻的并查集直接查询就行了。

Code

 #include<iostream>
 #include<cstring>
 #include<cstdio>
 #include<queue>
 #include<algorithm>
 #define N (200009)
 using namespace std;

 struct Edge{int to,next,len;}edge[N<<];
 struct Sgt{int ls,rs,v;};
 struct Line
 {
     int u,v,w,h;
     bool operator < (const Line &a) const {return h>a.h;}
 }l[N<<];
 struct Node
 {
     int num,dis;
     bool operator < (const Node &a) const {return dis>a.dis;}
 };
 int T,n,m,u,v,w,h,q,k,s,v0,p0,ans;
 int dis[N],head[N],num_edge;
 bool vis[N];
 priority_queue<Node>Q;

 struct Chairman_Tree
 {
     Sgt a[N*];
     int sgt_num,b[N],Root[N<<];

     int Build(int l,int r)
     {
         int now=++sgt_num;
         if (l==r) {a[now].v=b[l]; return now;}
         int mid=(l+r)>>;
         a[now].ls=Build(l,mid);
         a[now].rs=Build(mid+,r);
         return now;
     }
     int Update(int pre,int l,int r,int x,int v)
     {
         int now=++sgt_num;
         a[now].ls=a[pre].ls;
         a[now].rs=a[pre].rs;
         if (l==r) {a[now].v=v; return now;}
         int mid=(l+r)>>;
         if (x<=mid) a[now].ls=Update(a[now].ls,l,mid,x,v);
         else a[now].rs=Update(a[now].rs,mid+,r,x,v);
         return now;
     }
     int Query(int now,int l,int r,int x)
     {
         if (l==r) return a[now].v;
         int mid=(l+r)>>;
         if (x<=mid) return Query(a[now].ls,l,mid,x);
         else return Query(a[now].rs,mid+,r,x);
     }
 }Fa,Dep,Min;

 inline int read()
 {
     int x=; char c=getchar();
     while (c<'' || c>'') c=getchar();
     while (c>='' && c<='') x=x*+c-'', c=getchar();
     return x;
 }

 void add(int u,int v,int w)
 {
     edge[++num_edge].to=v;
     edge[num_edge].next=head[u];
     edge[num_edge].len=w;
     head[u]=num_edge;
 }

 int Find(int x,int t)
 {
     int fa=Fa.Query(Fa.Root[t],,n,x);
     return x==fa?x:Find(fa,t);
 }

 void Dijkstra(int s)
 {
     memset(dis,0x7f,sizeof(dis));
     memset(vis,,sizeof(vis));
     dis[s]=;
     Q.push((Node){s,});
     while (!Q.empty())
     {
         int x=Q.top().num; Q.pop();
         if (vis[x]) continue; vis[x]=;
         for (int i=head[x]; i; i=edge[i].next)
             if (!vis[edge[i].to] && dis[x]+edge[i].len<dis[edge[i].to])
             {
                 dis[edge[i].to]=dis[x]+edge[i].len;
                 Q.push((Node){edge[i].to,dis[edge[i].to]});
             }
     }
 }

 int main()
 {
     T=read();
     while (T--)
     {
         Fa.sgt_num=Dep.sgt_num=Min.sgt_num=;
         memset(head,,sizeof(head)); num_edge=;
         ans=;
         n=read(); m=read();
         for (int i=; i<=m; ++i)
         {
             u=read(); v=read(); w=read(); h=read();
             l[i]=(Line){u,v,w,h};
             add(u,v,w); add(v,u,w);
         }
         Dijkstra();
         sort(l+,l+m+);
         for (int i=; i<=n; ++i)
             Fa.b[i]=i, Dep.b[i]=, Min.b[i]=dis[i];
         Fa.Root[]=Fa.Build(,n);;
         Dep.Root[]=Dep.Build(,n);
         Min.Root[]=Min.Build(,n);
         for (int i=; i<=m; ++i)
         {
             Fa.Root[i]=Fa.Root[i-];
             Dep.Root[i]=Dep.Root[i-];
             Min.Root[i]=Min.Root[i-];
             int fx=Find(l[i].u,i),fy=Find(l[i].v,i);
             if (fx==fy) continue;
             int dfx=Dep.Query(Dep.Root[i],,n,fx);
             int dfy=Dep.Query(Dep.Root[i],,n,fy);
             if (dfx>dfy) swap(fx,fy);
             Fa.Root[i]=Fa.Update(Fa.Root[i],,n,fx,fy);
             int d1=Min.Query(Min.Root[i],,n,fx);
             int d2=Min.Query(Min.Root[i],,n,fy);
             Min.Root[i]=Min.Update(Min.Root[i],,n,fy,min(d1,d2));
             if (dfx==dfy) Dep.Root[i]=Dep.Update(Dep.Root[i],,n,fy,dfy+);
         }
         q=read(); k=read(); s=read();
         for (int i=; i<=q; ++i)
         {
             v0=read(); p0=read();
             v0=(v0+k*ans-)%n+;
             p0=(p0+k*ans)%(s+);
             int L=,R=m,A=-;
             while (L<=R)
             {
                 int mid=(L+R)>>;
                 if (l[mid].h>p0) A=mid,L=mid+;
                 else R=mid-;
             }
             if (A==-)
             {
                 printf("%d\n",dis[v0]);
                 ans=dis[v0]; continue;
             }
             int fx=Find(v0,A);
             ans=Min.Query(Min.Root[A],,n,fx);
             printf("%d\n",ans);
         }
     }
 }