数学：莫比乌斯反演-GCD计数

Luogu3455：莫比乌斯反演进行GCD计数

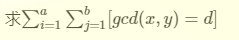
莫比乌斯反演就是用来解决这一类问题的，通常f函数是要求的那个，F函数是显然的

这样利用F的结果就可以推出来f的结果

在计算结果的时候整除分快儿一下就可以很快了

 #include<cstdio>
 #include<algorithm>
 using std::min;
 const int maxn=;
 int cnt;
 long long ans;
 bool vis[maxn];
 int mu[maxn],sum[maxn];
 long long prim[maxn];
 inline long long read()
 {
     long long x=,f=;char ch=getchar();
     while(ch<''||ch>'') {if(ch=='-')f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 void get_mu(long long x)
 {
     mu[]=;
     for(long long i=;i<=x;i++)
     {
         if(!vis[i]){mu[i]=-;prim[++cnt]=i;}
         for(long long j=;j<=cnt&&i*prim[j]<=x;j++)
         {
             vis[i*prim[j]]=;
             if(i%prim[j]==) break;
             else mu[i*prim[j]]=-mu[i];
         }
     }
     for(long long i=;i<=x;i++) sum[i]=sum[i-]+mu[i];
 }
 inline void init()
 {
     ans=;
 }
 int main()
 {
     int T;
     long long a,b,d,max_rep;
     T=read();
     get_mu();
     while(T--)
     {
         init();
         a=read();b=read();d=read();
         max_rep=min(a/d,b/d);
         for(long long l=,r;l<=max_rep;l=r+)
         {
             r=min(a/(a/l),b/(b/l));
             ans+=(a/(l*d))*(b/(l*d))*(sum[r]-sum[l-]);
         }
         printf("%lld\n",ans);
     }
     return ;
 }