CS229 6.18 CNN 的反向传导算法
本文主要内容是 CNN 的 BP 算法,看此文章前请保证对CNN有初步认识。
网络表示
CNN相对于传统的全连接DNN来说增加了卷积层与池化层,典型的卷积神经网络中(比如LeNet-5 ),开始几层都是卷积和池化的交替,然后在靠近输出的地方做成全连接网络,这时候已经将所有两维2D的特征maps转化为全连接的一维网络的输入。在前向传导或城中中,也只有两处与传统的 MLP 有所不同,分别是卷积层前向传导,与 pooling 传导到卷积层,如下图所示:
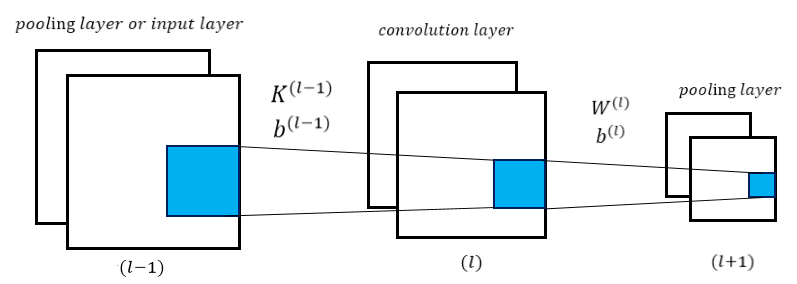
在上图中,层 (l−1)(l−1) 可以为pooling 层或是输入层,(l)(l) 层对 (l−1)(l−1) 层进行卷积操作,(l+1)(l+1) 对 (l)(l) 进行pooling操作。
符号表示
K(l−1)K(l−1):(l−1)(l−1) 层用到的卷积核,即(l−1)(l−1) 层的权值参数;
K(l−1)ijKij(l−1):从 (l−1)(l−1)层映射到 (l)(l) 层Feature Map j 所用到的卷积核 jj 的第 ii 个卷积模板;
b(l−1)b(l−1):(l−1)(l−1) 层的偏置参数;
b(l−1)jbj(l−1):映射到 (l)(l) 层中的 Feature Map j 的偏置参数;
w(l)w(l):表示 (l)(l) 层的参数;
w(l)jwj(l):卷积层第 j 个Feature Map 到 pooling 层第 j 个 Feature Map 是一一对应关系,即每个Feature Map 对应一个w(l)jwj(l);
b(l)b(l):(l)(l) 层的偏置参数;
b(l)jbj(l):卷积层第 j 个Feature Map 到pooling层第 j 个 Feature Map的偏置参数;
z(l)z(l):(l)(l) 层的输入;
a(l)a(l):(l)(l) 层的输出.
前向传导
CNN 的前向传导,首先从 (l−1)(l−1) 层到 (l)(l) 层,此处一般为多对多的形式,即对多个通道进行卷积操作,生成多个Feature Map,(l)(l)层第 j 个Feature Map的输入 z(l)jzj(l) 的计算如下:
需要注意:这里 z(l)j,a(l−1)i,K(l−1)ijzj(l),ai(l−1),Kij(l−1) 均为向量形式," * "表示卷积操作,z(l)jzj(l) 代表 第j 个 Feature Map 的输入,a(l−1)iai(l−1) 代表第 (l−1)(l−1) 层第 i 个 Feature Map的输出,Kl−1ijKijl−1 代表第 j 个卷积核中第 i 个卷积模板,要生成 (l)(l) 层的第 j 个Feature Map,需要对 (l−1)(l−1) 层的 MjMj 个通道同时进行卷积操作,对得到的结果加偏置求和即可。
第 (l)(l) 层的输出只需要对输入z(l)jzj(l) 做一个激活函数即可:
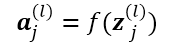
综上,从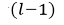 层 到
层 到 层可以用下图描述:
层可以用下图描述:
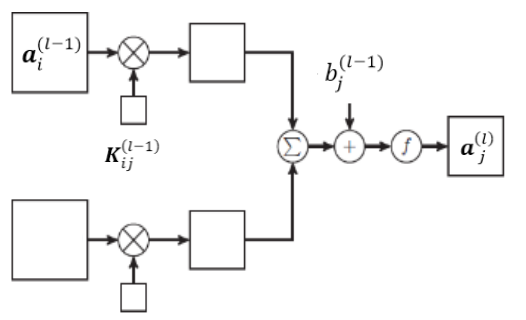
接下来从 到传导到第
到传导到第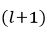 层,此处对应pooling 操作,一般为一对一的形式,
层,此处对应pooling 操作,一般为一对一的形式, 层的第 N 个 Feature Map 生成
层的第 N 个 Feature Map 生成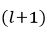 层的N个 Feature Map ,计算过程如下:
层的N个 Feature Map ,计算过程如下:
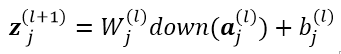
这里down(.)对应的是一个下采样(sub-sampling) 函数,这个函数会对 层的输出中的n-n的像素块进行pooling操作,使得输出在横纵方向都缩小n倍。经过down(.)操作后,
层的输出中的n-n的像素块进行pooling操作,使得输出在横纵方向都缩小n倍。经过down(.)操作后,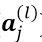 与
与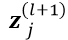 有相同的 size 根据以上公式计算
有相同的 size 根据以上公式计算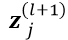 即可。同理,输出继续做一个映射:
即可。同理,输出继续做一个映射:
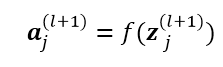
至此,前向传导过程已经可以求得,接下来与MLP类似,就是根据链式求导法则,求得残差的反向传导。
前馈 (Back Propagation)
对于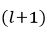 pooling 层,假设已知其第 j 个Feature Map 的残差向量
pooling 层,假设已知其第 j 个Feature Map 的残差向量 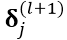 ,将其传导到
,将其传导到 ,即pooling层的误差传导到卷积层:
,即pooling层的误差传导到卷积层:
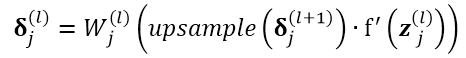
比如对于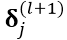 ,即
,即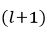 层的第 j 个 Feature Map 的残差项如下图左,对其做
层的第 j 个 Feature Map 的残差项如下图左,对其做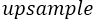 操作,得到下图右:
操作,得到下图右:
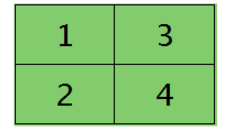
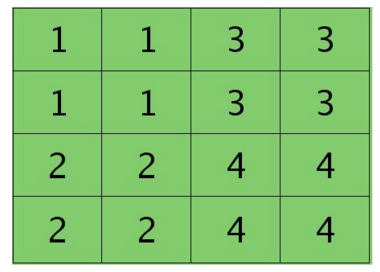
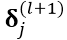
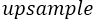 后
后
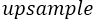 操作与
操作与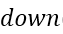 相反,
相反,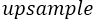 操作会还原
操作会还原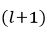 的残差map,使其与卷积层的map大小一致,即还原到down(.)之前的大小。这里残差为一对一传递,将层
的残差map,使其与卷积层的map大小一致,即还原到down(.)之前的大小。这里残差为一对一传递,将层  的map的激活函数的偏导数与从第
的map的激活函数的偏导数与从第 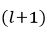 层的
层的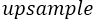 得到的残差map逐元素相乘,最后乘以参数
得到的残差map逐元素相乘,最后乘以参数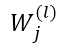 即可,注意这里
即可,注意这里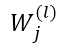 为一个常量,每个Feature Map j 对应一个参数
为一个常量,每个Feature Map j 对应一个参数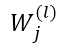 。
。
卷积层 与
与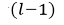 层一般为多对多的关系,根据以上分析求得了卷积层的残差项
层一般为多对多的关系,根据以上分析求得了卷积层的残差项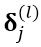 ,接下来就是卷积层的残差反向传导的过程。卷积层前面分两种情况,1)若卷积层前面为pooling层,则上面假设已知的
,接下来就是卷积层的残差反向传导的过程。卷积层前面分两种情况,1)若卷积层前面为pooling层,则上面假设已知的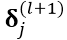 就是根据这里的推导所求得,并不是凭空出现。2)卷积层前面为初始输入。
就是根据这里的推导所求得,并不是凭空出现。2)卷积层前面为初始输入。
首先回忆卷积过程,卷积核 j 会对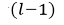 层多个通道进行卷积(每个通道对应 j 的一个卷积模板
层多个通道进行卷积(每个通道对应 j 的一个卷积模板 )求和,才会得到得到层
)求和,才会得到得到层  的第 j 个 Feature Map,所以
的第 j 个 Feature Map,所以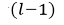 层的通道 i 的残差项应该由与之相关的层
层的通道 i 的残差项应该由与之相关的层  的所有Feature Map j 共同前向传导。假设与
的所有Feature Map j 共同前向传导。假设与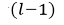 层的通道 i 相关的
层的通道 i 相关的  的所有Feature Map 共有 M 个,则有:
的所有Feature Map 共有 M 个,则有:
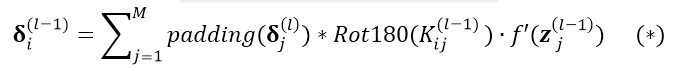
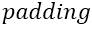 后做卷积的意思是完全卷积 假设输入图像 A 大小为 a x b,卷积核 B 大小为c x d,
后做卷积的意思是完全卷积 假设输入图像 A 大小为 a x b,卷积核 B 大小为c x d,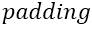 操作会对A进行填充,在 A 左右各填充(d-1)列,上下各填充(c-1)行,即
操作会对A进行填充,在 A 左右各填充(d-1)列,上下各填充(c-1)行,即 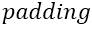 后 A 的大小变为( a+2c-2)x(b+2d-2),用B对
后 A 的大小变为( a+2c-2)x(b+2d-2),用B对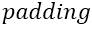 后的A做卷积,则卷积返回的大小为(a+b-1)x(a+b-1)。
后的A做卷积,则卷积返回的大小为(a+b-1)x(a+b-1)。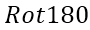 即为旋转180度。
即为旋转180度。
此处公式设计到卷积操作,形式比较复杂,下面引入一个示例来讲解上述公式:
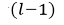 层的大小为 3 x 3,对
层的大小为 3 x 3,对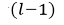 层的通道 i (为了便于说明,假设
层的通道 i (为了便于说明,假设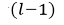 层为单通道),通过如下两个卷积核
层为单通道),通过如下两个卷积核 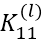 、
、 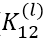 ,得到
,得到  层的两个Feature Map,假设其残差已经求得(前边已经讲过如何求卷积层的残差),残差分别为
层的两个Feature Map,假设其残差已经求得(前边已经讲过如何求卷积层的残差),残差分别为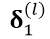
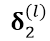 。
。
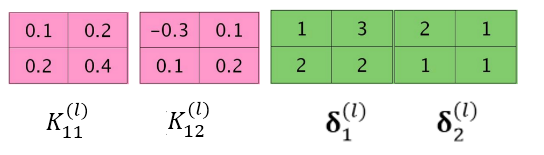
分别进行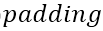 操作与
操作与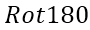 操作:
操作:
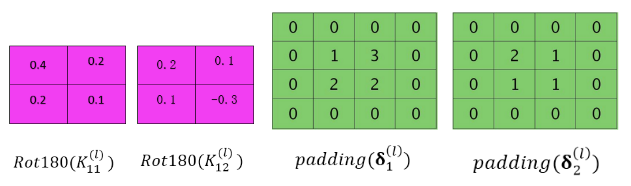
将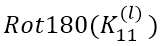 与
与 进行卷积,
进行卷积,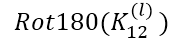 与
与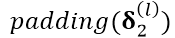 进行卷积:
进行卷积:

注意此处不考虑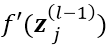 项(或者认为是线性激活 即
项(或者认为是线性激活 即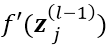 = 1),对结果求和有:
= 1),对结果求和有:
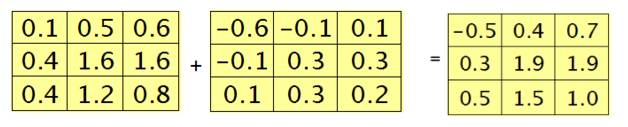
以上过程即完成了整个公式 的计算,为什么这么计算呢?可以把以上过程展开,把
的计算,为什么这么计算呢?可以把以上过程展开,把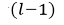 与
与  展开为全连接的形式,(此处清楚起见,只写了
展开为全连接的形式,(此处清楚起见,只写了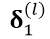 ),根据MLP中误差按权值平均反向传导的形式 可求得
),根据MLP中误差按权值平均反向传导的形式 可求得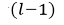 层的残差
层的残差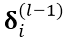 ,其实归根到底还是MLP得形式。
,其实归根到底还是MLP得形式。
求解网络参数的导数
至此,关于CNN中的输入前向传导与残差的后向反馈全部计算完成,下面可以根据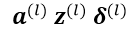 来对网络的权值
来对网络的权值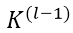
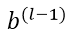
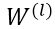
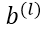 进行求导。
进行求导。
假设当前损失函数为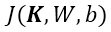
1)对于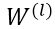
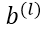 ,根据链式求导法则:
,根据链式求导法则:
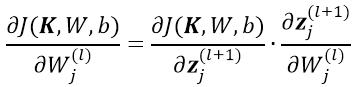
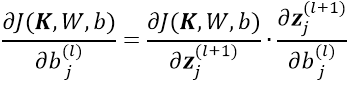
根据残差的定义与前边的计算公式:
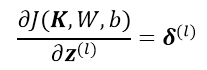
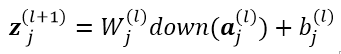
可得到如下公式,公式中的累加是因为 conv 层中 n *n 的区域变为 1个 1*1 的 pooling 元素,但是 这 n*n 的权值取值是一样的,所以对该权值求导是 pooling 层所有节点的累加:
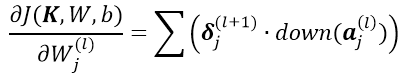
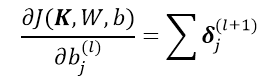
这里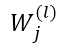
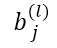 均为实数,且
均为实数,且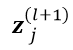 中的所有元素的参数均为
中的所有元素的参数均为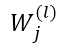
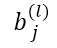 ,所以对结果向量进行求和操作。这里的
,所以对结果向量进行求和操作。这里的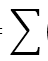 代表对
代表对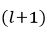 层Feature Map j 中的所有元素求和
层Feature Map j 中的所有元素求和
2)对于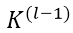
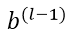 ,根据链式求导法则:
,根据链式求导法则:
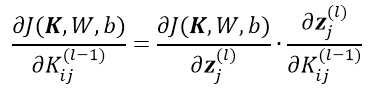
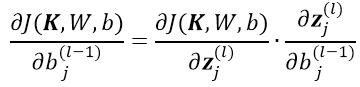
根据残差的定义与前边的计算公式:
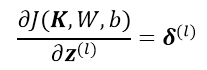
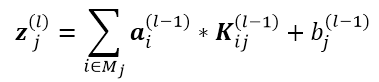
可得:
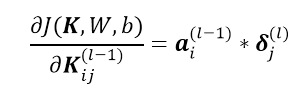
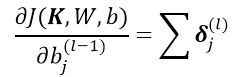
同样通过一个实例说明关于卷积核的偏导数求解过程,对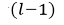 层的通道 i 用卷积核
层的通道 i 用卷积核 进行卷积操作,得到
进行卷积操作,得到 层的 Feature Map j,其残差
层的 Feature Map j,其残差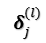 已经求得,对于下图左的卷积过程展开,下图右为展开后:
已经求得,对于下图左的卷积过程展开,下图右为展开后:
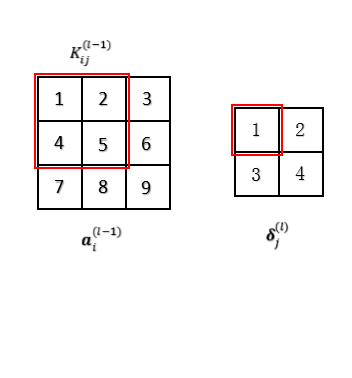
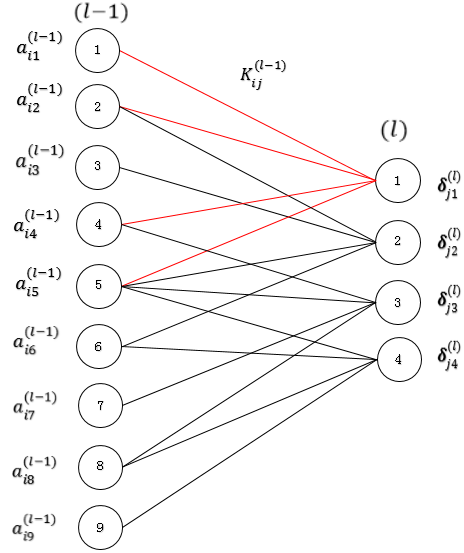
注意这里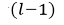 层的节点① ② ④ ⑤ 用卷积核
层的节点① ② ④ ⑤ 用卷积核 卷积生成生成
卷积生成生成 层的节点①,即
层的节点①,即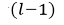 层的节点① ② ④ ⑤ 与
层的节点① ② ④ ⑤ 与 层的节点①通过权值
层的节点①通过权值 相连,分别为
相连,分别为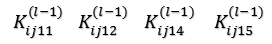 回忆传统的MLP网络的参数求导公式:
回忆传统的MLP网络的参数求导公式:
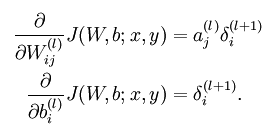
所以这里有对于单个 层的节点①对应的权值求导有:
层的节点①对应的权值求导有:
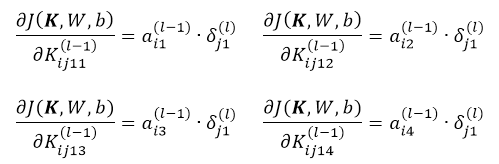
考虑 层的节点② ③ ④对应的权值与节点①对应的权值相等(用的同一卷积核
层的节点② ③ ④对应的权值与节点①对应的权值相等(用的同一卷积核 ):所以可以忽略
):所以可以忽略 节点对应的下标:
节点对应的下标:
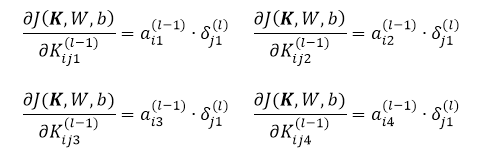
同样分别对节点 层的节点② ③ ④对应的权值求导,比如对于节点 ④:
层的节点② ③ ④对应的权值求导,比如对于节点 ④:
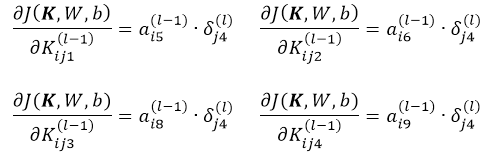
最终将偏导数项相加有:
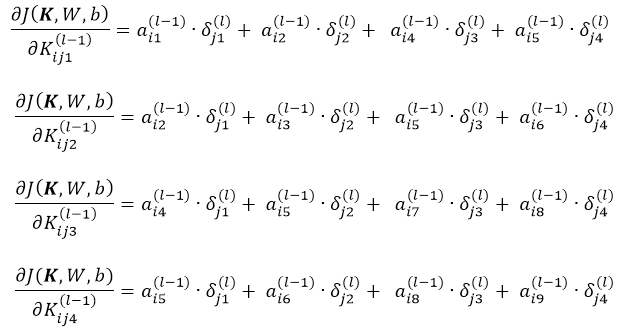
下图描述了以上过程,等等,仔细观察一下以上公式,这不就是用 层残差Map 对
层残差Map 对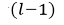 层的输出
层的输出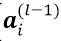 做卷积吗?oh my god,
做卷积吗?oh my god, 的导数可以通过对
的导数可以通过对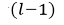 层的输出
层的输出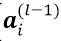 与卷积层
与卷积层 的残差矩阵卷积得到!!
的残差矩阵卷积得到!!
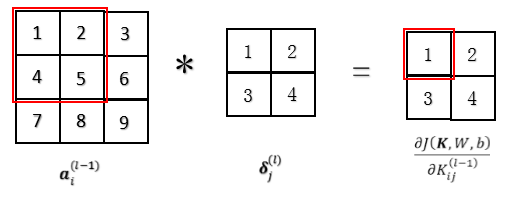 、
、
总结以上公式综上所述:
1)任意层前向传到到卷积层与卷积层前向传导到pooling层
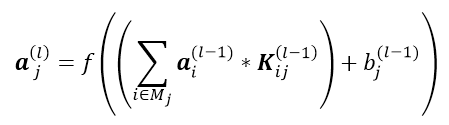
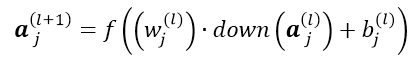
2)pooling层前馈到卷积层,与卷积层前馈到任意层
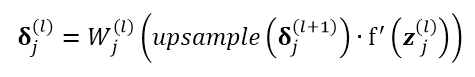
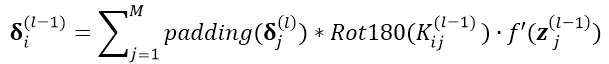
3)任意层与卷积层之间参数的求导
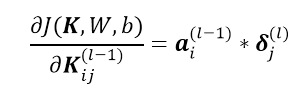
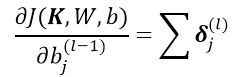
4)pooling层与卷积层之间参数的求导
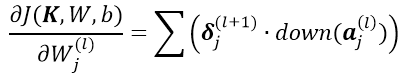
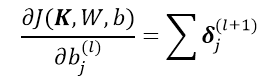
一些复杂的卷积操作matlab函数('valid' 与 'full' 表示的卷积模式不同):
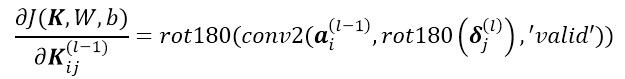
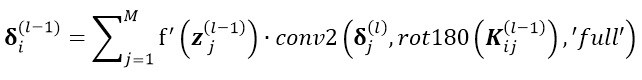
至此,CNN中的前后向传导的过程全部推倒完毕,其实万变不离其宗,归根到底还是MLP那一套BP算法,接下来就是实现CNN了,也就是cs231n的作业。
参考:
Notes on Convolutional Neural Networks,Jake Bouvrie
http://www.cnblogs.com/tornadomeet/p/3468450.html
http://blog.csdn.net/zouxy09/article/details/9993371
CS229 6.18 CNN 的反向传导算法的更多相关文章
- (六)6.18 cnn 的反向传导算法
本文主要内容是 CNN 的 BP 算法,看此文章前请保证对CNN有初步认识,可参考Neurons Networks convolutional neural network(cnn). 网络表示 CN ...
- UFLDL 教程学习笔记(二)反向传导算法
UFLDL(Unsupervised Feature Learning and Deep Learning)Tutorial 是由 Stanford 大学的 Andrew Ng 教授及其团队编写的一套 ...
- 卷积神经网络(CNN)反向传播算法
在卷积神经网络(CNN)前向传播算法中,我们对CNN的前向传播算法做了总结,基于CNN前向传播算法的基础,我们下面就对CNN的反向传播算法做一个总结.在阅读本文前,建议先研究DNN的反向传播算法:深度 ...
- 卷积神经网络(CNN)前向传播算法
在卷积神经网络(CNN)模型结构中,我们对CNN的模型结构做了总结,这里我们就在CNN的模型基础上,看看CNN的前向传播算法是什么样子的.重点会和传统的DNN比较讨论. 1. 回顾CNN的结构 在上一 ...
- 反向传播算法 Backpropagation Algorithm
假设我们有一个固定样本集,它包含 个样例.我们可以用批量梯度下降法来求解神经网络.具体来讲,对于单个样例(x,y),其代价函数为:这是一个(二分之一的)方差代价函数.给定一个包含 个样例的数据集,我们 ...
- 神经网络训练中的Tricks之高效BP(反向传播算法)
神经网络训练中的Tricks之高效BP(反向传播算法) 神经网络训练中的Tricks之高效BP(反向传播算法) zouxy09@qq.com http://blog.csdn.net/zouxy09 ...
- 循环神经网络(RNN)模型与前向反向传播算法
在前面我们讲到了DNN,以及DNN的特例CNN的模型和前向反向传播算法,这些算法都是前向反馈的,模型的输出和模型本身没有关联关系.今天我们就讨论另一类输出和模型间有反馈的神经网络:循环神经网络(Rec ...
- (3)Deep Learning之神经网络和反向传播算法
往期回顾 在上一篇文章中,我们已经掌握了机器学习的基本套路,对模型.目标函数.优化算法这些概念有了一定程度的理解,而且已经会训练单个的感知器或者线性单元了.在这篇文章中,我们将把这些单独的单元按照一定 ...
- CNN的反向传播
在一般的全联接神经网络中,我们通过反向传播算法计算参数的导数.BP 算法本质上可以认为是链式法则在矩阵求导上的运用.但 CNN 中的卷积操作则不再是全联接的形式,因此 CNN 的 BP 算法需要在原始 ...
随机推荐
- Java NIO Reactor模式
一.NIO介绍: NIO模型: 1.Channel为连接通道,相当于一个客户端与服务器的一个连接,Selector为通道管理器,将Channel注册到Selector上,Selector管理着这些Ch ...
- Mysql5.6 for Centos6.5源码编译安装
## 说明 不同服务器需要改变 server_id ,同一台机器上需要改变 port 1. 关闭防火墙[root@mysql ~]# service iptables status --查看防火墙状态 ...
- Java变量的初始值
Java中的变量如果没有赋值,成员变量默认被初始化,局部变量则不会. 对于成员变量 int a; // a的初始值为0 如下例中的成员变量a,b,c,d public class Va ...
- java项目发布
一.使用eclipse把项目以war格式导出 二.把war文件放在tomcat的webapps中 三.在tomcat的conf文件夹里的server.xml进行配置: 在<Host>< ...
- linux curl 命令的使用
有时候需要内网访问接口地址,使用curl命令,带上-v参数 -v 参数可以显示一次 http 通信的整个过程,包括端口连接和 http request 头信息 curl -v http://172.9 ...
- hadoop商业版本的选择介绍
记得刚接触到hadoop的时候跟大部分人一样都会抱怨hadoop的安装部署问题,对于一个新手来说这这的是个头疼的问题,可能需要花费一整天的时间才能把分布式环境安装配置好.在刚接触hadoop的一段时间 ...
- Linux paste命令详解
Linux paste命令 Linux paste命令用于合并文件的列.paste指令会把每个文件以列对列的方式,一列列地加以合并 将每个指定文件里的每一行整合到对应一行里写到标准输出,之间用制表符分 ...
- ajaxFileupload 多文件上传
ajaxFileupload 多文件上传 修改前的代码: var oldElement = jQuery('#' + fileElementId); var newElement = jQuery(o ...
- SDI初识
SDI初识 SDI接口,即“数字分量串行接口(Serial Digital Interface)”.按照速率可以分为: 标准清晰度SD-SDI,速率为270Mb/s; 高清标准HD-SDI,速率为1. ...
- TableLayoutPanel 行高列宽设置
/// <summary> /// 获取TableLayoutPanel指定行的高度 /// </summary> /// <param name="layou ...
