Andrew Ng - 深度学习工程师 - Part 2. 改善深层神经网络:超参数调试、正则化以及优化(Week 2. 优化算法)
===========第2周 优化算法================
===2.1 Mini-batch 梯度下降===
epoch: 完整地遍历了一遍整个训练集
===2.2 理解Mini-batch 梯度下降===
Mini-batch=N,Batch GD。训练集小(<=2000),选Bath;
Mini-batch=1,Stochastic GD。不会收敛,而是一直在最小值附近“波动”。噪声可以通过减小学习率在一定程度上得到减缓,但每次只处理一个样本,失去了向量化带来的好处
考虑到计算机存储方式,通常选择mini-batch为2的指数,使得代码运行更快,最常见的是64,128,512。 In practice,mini-bacth的大小也是一个超参,做一个快速check,看哪一个可以最有效地降低代价函数值
注意使你的Bath大小与你的CPU/GPU内存相符
===2.3 指数加权平均===
Exponentially weighted averages: Vt = beta * Vt-1 + (1-beta) Zt, 比如 beta=0.9
可以review video中Andrew对beta取下面三个不同值时,温度曲线的不同
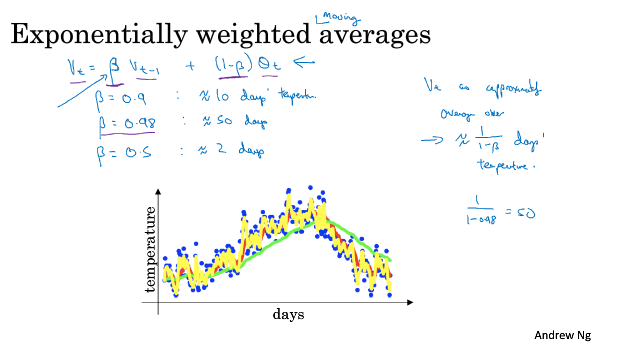
===2.4 理解指数加权平均===
【维基百科】https://en.wikipedia.org/wiki/Moving_average
===2.5 指数加权平均的偏差估计===
在机器学习中,在实现指数加权平均的时候,大家不在乎执行偏差修正,因为大部分人would rather just 熬过初始。但如果你关心初始时期的偏差,那么你在刚计算的时候就要使用偏差修正。

===2.6 动量梯度下降===
Momentum:对梯度做指数加权平均。Momentum总是好于简单的梯度下降。
我们总是希望在梯度较缓的地方走长一点,在梯度很陡的地方走慢一点。
通常取beta=0.9是一个很鲁棒的值,当然也可以调参。实践中人们通常不进行偏差修正,因为10次之后基本就不会有明显偏差了。
===2.7 RMSprop===
Root Mean Square prop
跟Mmomentum类似,RMSprop也可以消除梯度下降中的摆动,并允许你使用一个更大的学习率。
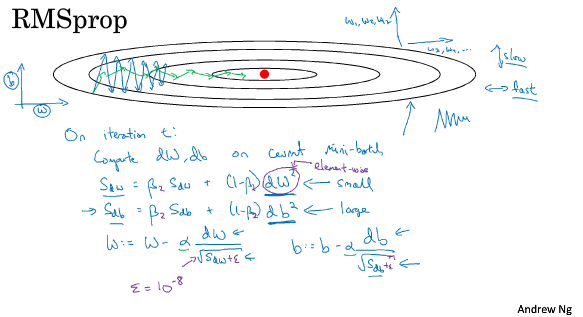
===2.8 Adam===
Adaptive Moment Estimation
通常学习率alpha需要调参,而默认beta_1=0.9, beta_2=0.99,

===2.9 学习率衰减===
learning rate decay, 有好几个可选的形式
比如随着epco衰减 1/(1+decay_rate*epoch_num),decay_rate是超参,其他的还有 指数衰减 decay_rate^epoch_num, k / sqrt(epoch_num) ,离散下降等等
when training only a small number of models,有些人也会手动调整学习率
For me, I would say that learning rate decay usually lower down on the list of things I try,Setting alpha, just a fixed value of alpha, and getting that to be well tuned, has a huge impact. Learning rate decay does help. Sometimes it can really help speed up training, but it is a little bit lower down my list in terms of the things I would try.(但这并不会是我率先尝试的内容)
===2.10 局部最优的问题===
想象一幅我们关于有多个局部最优值的三维直觉图,第三维是代价函数值,事实证明,当维数低的时候(权重是2维),很容易出现这样的图。
但这样的直觉对高维来说并不是正确的,我们发现most梯度为零的点通常是“鞍点”,而不是我们所想象的局部极小值。可以很容易理解,比如一个有20,000权重的模型,画出代价函数关于权重的图,局部极小值意味着,关于20,000每个权重的方向,该点都是碗状的,这样的点其实非常少。
在深度学习的历史中,我们学到的一课时我们对低维空间的大部分直觉并不能应用到高维空间中。
Problem of plateaus. It turns out that 平稳段 can really slow down the learning。And and a plateau is a region where the derivative is close to zero for a long time.
Momentum,RMSprop,Adam这些优化算法对处理Plateanus有一定的好处
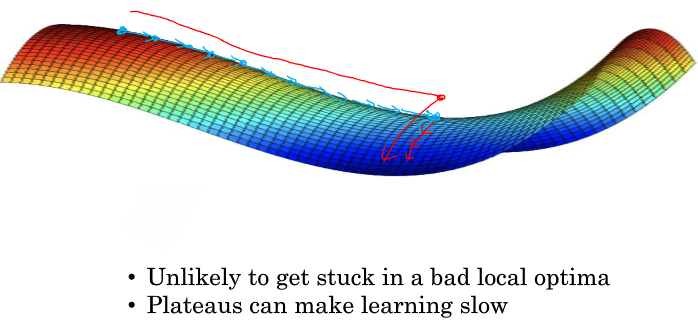
Andrew Ng - 深度学习工程师 - Part 2. 改善深层神经网络:超参数调试、正则化以及优化(Week 2. 优化算法)的更多相关文章
- Andrew Ng - 深度学习工程师 - Part 1. 神经网络和深度学习(Week 1. 深度学习概论)
=================第1周 循环序列模型=============== ===1.1 欢迎来到深度学习工程师微专业=== 我希望可以培养成千上万的人使用人工智能,去解决真实世界的实际问 ...
- Andrew Ng - 深度学习工程师 - Part 1. 神经网络和深度学习(Week 4. 深层神经网络)
=================第2周 神经网络基础=============== ===4.1 深层神经网络=== Although for any given problem it migh ...
- Andrew Ng - 深度学习工程师 - Part 1. 神经网络和深度学习(Week 3. 浅层神经网络)
=================第3周 浅层神经网络=============== ===3..1 神经网络概览=== ===3.2 神经网络表示=== ===3.3 计算神经网络的输出== ...
- Andrew Ng - 深度学习工程师 - Part 1. 神经网络和深度学习(Week 2. 神经网络基础)
=================第2周 神经网络基础=============== ===2.1 二分分类=== ===2.2 logistic 回归=== It turns out, whe ...
- 《Andrew Ng深度学习》笔记1
深度学习概论 1.什么是神经网络? 2.用神经网络来监督学习 3.为什么神经网络会火起来? 1.什么是神经网络? 深度学习指的是训练神经网络.通俗的话,就是通过对数据的分析与计算发现自变量与因变量的映 ...
- 《Andrew Ng深度学习》笔记4
浅层神经网络 1.激活函数 在神经网络中,激活函数有很多种,常用的有sigmoid()函数,tanh()函数,ReLu函数(修正单元函数),泄露ReLu(泄露修正单元函数).它们的图形如下: sigm ...
- Coursera Deep Learning笔记 改善深层神经网络:超参数调试 正则化以及梯度相关
笔记:Andrew Ng's Deeping Learning视频 参考:https://xienaoban.github.io/posts/41302.html 参考:https://blog.cs ...
- 《Andrew Ng深度学习》笔记2
神经网络基础 1.图计算 计算时有两种方法:正向传播和反向传播.正向传播是从底层到顶层的计算过程,逐步推出所求公式.反向传播是从顶层到底层,从已知的式子求出因变量的影响关系. 在这里用到的反向传播算法 ...
- 《Andrew Ng深度学习》笔记5
深层神经网络 深层神经网络的组成如图,这里主要是深层神经网络符号的定义. 为什么要用深层神经网络,有什么好处?这里主要是分层的思想.在软件工程中,如果问题遇到困难,一般是通过“加多”一层的方法来解决, ...
随机推荐
- SpringBoot自定义装配的多种实现方法
Spring手动装配实现 对于需要加载的类文件,使用@Configuration/@Component/@Service/@Repository修饰 @Configuration public cla ...
- 集合框架之ArrayList -Java
ArrayList 1.与数组的区别 如果要存放多个对象,可以使用数组,但是数组会有长度的限制,会出现不够用或者是浪费的情况. 为了解决数组的局限性引入了容器的概念,最常用的容器就是ArrayList ...
- 0512String类
String类 2. String类 2.1 字符串类型概述 又爱又恨!!! 爱: 字符串基本上就是数据的保存,传输,处理非常重要的一种手段. 恨: 解析过程非常烦人,需要掌握熟记很多方法,同时需要有 ...
- Java基本语法---标识符、变量、数据类型转换及进制
Java基本语法 标识符 标识符:凡事可以自己起名字的地方,都可以叫做标志符 标识符命名规则: 26个字母大小写,数字0-9,下划线_,美元符号$ 数字不能开头 不能使用关键字和保留字,但是可以包含 ...
- [C#] [VS] Snippets快捷代码块之 Region
代码长了,阅读起来不方便, 于是,C#中我们经常会用 region来折叠代码块. 在VS中,输入 #region , 点Tab,会自动生成如下: #region MyRegion #endregion ...
- [wordpress使用]004_导入多媒体
在写文章的时候难免要需要用到图片.音频或者视频文件,wordpress不仅提供本地上传多媒体文件功能,更提供在线导入多媒体.能更方便,范围更大的获取我们所需要的资源. 本地上传文件 在写文章的界面,选 ...
- 读Pyqt4教程,带你入门Pyqt4 _011
当我们想要改变或者增强已存在的窗口组件时,或者准备从零开始创建自定义窗口组件时,可以使用绘图.我们通过使用PyQt4工具包提供的绘图API来绘图. 绘图在 paintEvent() 方法中进行.绘制代 ...
- C# 委托浅析
C# 中的委托(Delegate)类似于 C 或 C++ 中函数的指针.委托(Delegate) 是存有对某个方法的引用的一种引用类型变量.引用可在运行时被改变. 委托(Delegate)特别用于实现 ...
- 数据库之 MySQL --- 数据处理 之 表的约束与分页(七)
个人博客网:https://wushaopei.github.io/ (你想要这里多有) 1.约束 :为了保证数据的一致性和完整性,SQL规范以约束的方式对表数据进行额外的条件限制 ...
- ASP.NET中使用Entity Framework开发增删改查的Demo(EF增删改查+母版页的使用)
这里更多的是当作随身笔记使用,记录一下学到的知识,以便淡忘的时候能快速回顾 这里是该项目的第二部分, 第一部分 第二部分(当前部分) 大完结版本 此Demo是新建了一个音乐类型的web,然后使用母版页 ...
