[洛谷P3391] 文艺平衡树 (Splay模板)

初识splay

学splay有一段时间了，一直没写......

本题是splay模板题，维护一个1~n的序列，支持区间翻转（比如1 2 3 4 5 6变成1 2 3 6 5 4），最后输出结果序列。

模板题嘛......主要了解一下splay的基本操作QwQ

原题地址链接[洛谷P3391文艺平衡树]

1.基本概念

splay是一种二叉搜索树，节点的权值满足lson<p<rson，故可以像其他二叉搜索树一样在树上二分查找某数排名，排名为k的数，以及前驱后继等。

普通的二叉搜索树在面对特殊数据时树的深度会从log n退化成接近n（退化成链），这样操作的时间复杂度会从O（log n）退化成O（n），影响效率。

splay通过旋转维持树的平衡。这个操作后面会提到。

2.基本操作

二叉搜索树的基本操作：求排名为k的数。

 int rank(int p,int k)
 {
     pushdown(p);
     if(k<=sz[s[p][]])
         return rank(s[p][],k);
     else if(k==sz[s[p][]]+)
         return p;
     else
         return rank(s[p][],k-sz[s[p][]]-);
 }

简单的树上二分。

3.核心操作：splay

splay的精髓在于骚气的旋转。（名字就是这么来的哈哈哈~）

splay的核心操作是splay（一脸懵逼），splay（x，y）意为通过一系列旋转，将点x旋转到点y下面，使x成为y的儿子。

每次旋转通过rotate函数实现：

 void rotate(int p)
 {
     int fa=f[p];
     bool k=id(p);
     s[fa][k]=s[p][!k];
     s[p][!k]=fa;
     s[f[fa]][id(fa)]=p;
     f[p]=f[fa];
     f[s[fa][k]]=fa;
     f[fa]=p;
     refresh(fa);
     refresh(p);
 }

rotate的时候严格满足splay二叉搜索树的性质：lson<p<rson。

将p提到fa的位置，根据大小关系决定fa是作为p的左儿子还是右儿子，这样实际上是fa挤掉了p原先的某个儿子，而p转上去，让出了fa的一个儿子的位置。

所以最后让那个被fa挤掉的p的孤儿作为fa的某个儿子，填到空缺的地方去（原来p的位置）。

至于splay的实现方法...有两种：单旋和双旋。

单旋即无脑地一直转，直到把x转到y下面。

 void splay(int p,int g)  // 单旋
 {
     while(f[p]!=g)rotate(p);
     if(!g)root=p;
 }

比起单旋，双旋能更好的维护splay的平衡。

 void splay(int p,int g) // 双旋
 {
     while(f[p]!=g)
     {
         int fa=f[p];
         if(f[fa]==g)
         {
             rotate(p);
             break;
         }
         if(id(p)^id(fa))rotate(p);
         else rotate(fa);
         rotate(p);
     }
     if(!g)root=p;
 }

利用splay操作，我们就可以用这棵树实现很多其它平衡树实现不了的功能。

4.元素的插入、删除、查询及修改

设x为 要插入的/要删除的/要查询的/要修改的 元素or区间。

进行这些操作之前，运用旋转操作把x的前驱pre转到根位置，把x的后继post转到根的下面，post>pre，所以此时post一定是pre的右儿子。

（如果是区间，pre就是left的前驱，post就是right的后继）

如图：

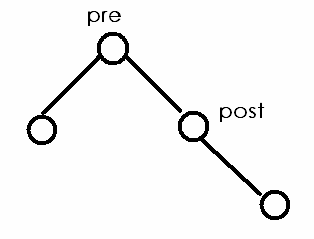
此时，根据二叉搜索树的性质，要删除/查询/修改的元素or区间就一定在post的左子树那里。如图：（目标子树：红色部分）

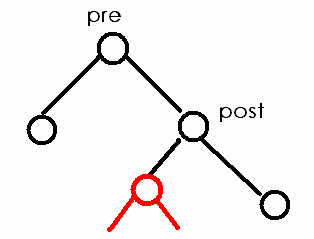
4.1 插入

如果是插入，红色部分一定为空，在那里插入即可。

4.2 删除

残忍抛弃红色部分。

4.3 查询

在红色部分查询。

4.4 修改

在这道题里是区间翻转。

我们并不需要真的翻转，打个标记就行。

标记需要下传的时候，交换左右子树的左右子树，在左右儿子上打标记，清掉自身标记。

 void pushdown(int p)
 {
     if(!fl[p])return;
     fl[s[p][]]^=;
     fl[s[p][]]^=;
     swap(s[s[p][]][],s[s[p][]][]);
     swap(s[s[p][]][],s[s[p][]][]);
     fl[p]=;
 }

这样就行了。

完事了？

完事了。

最后二分输出序列即可。

其他细节见代码。

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #define N 100005
 #define id(x) (s[f[x]][1]==x) // 判断是左儿子还是右儿子
 using namespace std;

 int f[N],s[N][],val[N],sz[N],root,tot; // 分别是父亲，儿子，值，子树大小，树根，元素数量
 bool fl[N]; // 翻转标记

 void refresh(int p) // 更新size
 {
     sz[p]=sz[s[p][]]+sz[s[p][]]+;
 }

 void pushdown(int p) // 下传标记
 {
     if(!fl[p])return;
     fl[s[p][]]^=;
     fl[s[p][]]^=;
     swap(s[s[p][]][],s[s[p][]][]);
     swap(s[s[p][]][],s[s[p][]][]);
     fl[p]=;
 }

 void rotate(int p) // 把p转上去
 {
     int fa=f[p];
     bool k=id(p);
     s[fa][k]=s[p][!k];
     s[p][!k]=fa;
     s[f[fa]][id(fa)]=p;
     f[p]=f[fa];
     f[s[fa][k]]=fa;
     f[fa]=p;
     refresh(fa);
     refresh(p);
 }
 /*
 void splay(int p,int g) // 单旋
 {
     while(f[p]!=g)rotate(p);
     if(!g)root=p;
 }
 */
 void splay(int p,int g) // 双旋
 {
     while(f[p]!=g)
     {
         int fa=f[p];
         if(f[fa]==g)
         {
             rotate(p);
             break;
         }
         if(id(p)^id(fa))rotate(p);
         else rotate(fa);
         rotate(p);
     }
     if(!g)root=p;
 }

 int rank(int p,int k) // 查询rank为k的元素
 {
     pushdown(p);
     if(k<=sz[s[p][]])
         return rank(s[p][],k);
     else if(k==sz[s[p][]]+)
         return p;
     else
         return rank(s[p][],k-sz[s[p][]]-);
 }

 int build(int l,int r,int fa) // 建树  实际上一个一个插入也行，但是这样二分建树可以使初始树更平衡
 {
     if(l>r)return ;
     int mid=(l+r)>>;
     int p=++tot;
     s[p][]=build(l,mid-,p);
     s[p][]=build(mid+,r,p);
     val[p]=mid;
     f[p]=fa;
     refresh(p);
     return p;
 }

 void change(int l,int r) // 区间翻转
 {
     int pre,post,rt;
     pre=rank(root,l-);
     splay(pre,);
     post=rank(root,r+);
     splay(post,pre);
     rt=s[post][];
     swap(s[rt][],s[rt][]);
     fl[rt]^=;
 }

 void print(int p) // 二分输出结果序列
 {
     if(!p)return;
     pushdown(p);
     print(s[p][]);
     printf("%d ",val[p]);
     print(s[p][]);
 }

 int n,m;

 int main()
 {
     scanf("%d%d",&n,&m);
     root=build(,n+,);
     for(int i=;i<=m;i++)
     {
         int lb,rb;
         scanf("%d%d",&lb,&rb);
         change(lb+,rb+);
     }
     splay(rank(root,),);
     splay(rank(root,n+),root);
     print(s[s[root][]][]);
     return ;
 }

 complete code of splay tree

complete code of splay tree