CodeForces 990D Graph And Its Complement（图和补图、构造）

http://codeforces.com/problemset/problem/990/D

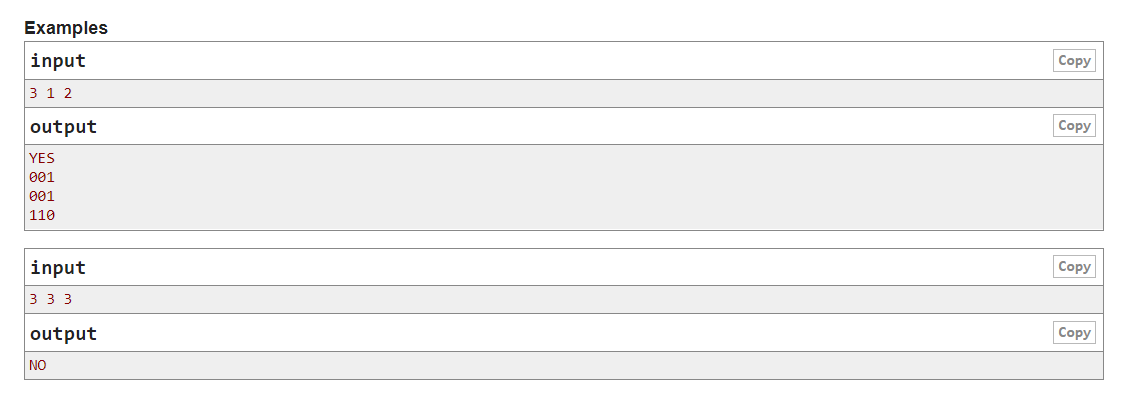
题意：

构造一张n阶简单无向图G，使得其连通分支个数为a，且其补图的连通分支个数为b。

题解：

第一眼看到题，一脸懵，嗯？这让我怎么建图？？？

还是菜啊，看别人的题解学习学习吧。。。

参考于：https://www.cnblogs.com/siuginhung/p/9172602.html

这是一个构造问题。

对于一张n阶简单无向图G，若此图不连通，则其补图是连通的。

证明：

首先，在简单无向图G中，若结点u、v（u≠v）不连通，则在其补图中，u、v必然连通。

将图G=<V,E>划分为k个连通分支，Gi=<Vi,Ei>，i=1,2,...,k。在V中任取两点u、v（u≠v）。

若u∈Vi，v∈Vj，且i≠j，则u、v在图G中不连通，则u、v必然在其补图中连通；

若u,v∈Vi，则必然存在w∈Vj，且i≠j，使得u、w和v、w在补图中连通。

于是，在题中，a、b中至少有一个为1。

接下来构造连通分支：若一个n阶简单无向图有k（k≥2）个连通分支，则可以构造其连通分支分别为{1},{2},...,{k-1},{k,k+1,...,n}。

代码如下：

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <string>
 #include <math.h>
 #include <algorithm>
 #include <vector>
 #include <stack>
 #include <queue>
 #include <set>
 #include <map>
 #include <sstream>
 const int INF=0x3f3f3f3f;
 typedef long long LL;
 #define Bug cout<<"---------------------"<<endl
 const int mod=1e9+;
 const int maxn=2e5+;
 using namespace std;

 int G[][];

 int main()
 {
     int n,a,b;
     scanf("%d %d %d",&n,&a,&b);
     if((a!=&&b!=)||(n==||n==)&&(a==&&b==))
         printf("NO\n");
     else
     {
         printf("YES\n");
         if(a==)
         {
             for(int i=;i<=n;i++)
             {
                 G[i][i]=;
                 for(int j=i+;j<=n;j++)
                     G[i][j]=G[j][i]=;
             }
             for(int i=b;i<n;i++)
                 G[i][i+]=G[i+][i]=;
         }
         else
         {
             memset(G,,sizeof(G));
             for(int i=a;i<n;i++)
             {
                 G[i][i+]=G[i+][i]=;
             }
         }
         for(int i=;i<=n;i++)
         {
             for(int j=;j<=n;j++)
                 printf("%d",G[i][j]);
             printf("\n");
         }
     }
     return ;
 }