POJ 1330 Nearest Common Ancestors / UVALive 2525 Nearest Common Ancestors （最近公共祖先LCA）

Description

A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:

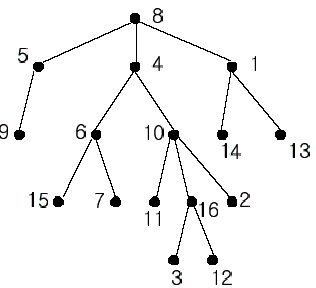
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.

For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.

Write a program that finds the nearest common ancestor of two distinct nodes in a tree.

Input

The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N. Each of the next N -1 lines contains a pair of integers that represent an edge --the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N - 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.

Output

Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.

Sample Input

2

16

1 14

8 5

10 16

5 9

4 6

8 4

4 10

1 13

6 15

10 11

6 7

10 2

16 3

8 1

16 12

16 7

5

2 3

3 4

3 1

1 5

3 5

Sample Output

4

3

Http

POJ:https://vjudge.net/problem/POJ-1330

UVAlive:https://vjudge.net/problem/UVALive-2525

Source

最近公共祖先，LCA

题目大意

给出一棵树，求两点之间的公共祖先。

解决思路

求LCA有多种方法，那么本题我们用在线的倍增算法。

倍增算法基于的是非常高效的二分思想，即二分两个点的祖先，看是否是共同祖先，若是，则寻找更近的，若不是，则寻找更远的。

那么为了实现这个二分，我们定义一个Parent数组，Parent[u][i]表示u的(1 << i)祖先（即2^{i祖先），为什么要选择2}i呢，因为我们用的是二分嘛。

另外，为了方便后面倍增，我们再定义一个Depth[u]数组表示u的深度。

那么首先我们用一个dfs求出Depth[u]和parent[u][0]（即u的父亲，这是可以在dfs中求出来的）

然后，我们求出Parent的其他数组，Parent[u][i]=Parent[Parent[u][i-1]][i-1]，这个很显然，u的2^{i祖先就是u的2}(i-1)祖先的2^(i-1)祖先（自己可以手动模拟一下）

有了上面求出来的两组信息，我们就可以在线地求LCA啦。

现在假设我们要求LCA的是两个点a和b，并且Depth[a]>Depth[b]（如果不是怎么办，swap(a,b)就可以了）。

那么，我们的第一步是把a与b提升到同一高度，这个较好理解。让k从大（一般是20）到小（0）循环，每次判断Depth[Parent[a][k]]与Depth[b]的大小关系，若Depth[Parent[a][k]]==Deptf[b]，则a=Parent[a][k]，相当于把a向上翻。

在a与b到达同一高度后，若此时ab说明已经找到了a,b的公共祖先，直接输出即可。若还不是，则把二者同时向上翻。注意，为了保证求得的是最近的公共祖先，这里的if判断不能写Parent[a][k]Parent[b][k]，而要写Parent[a][k]!=Parent[b][k]（自己想一想，为什么）

最后求得的解就是Parent[a][0]（或者是Parent[b][0]，两者是一样的）

LCA还有一些细节的地方需要注意，具体请看代码（都用注释标记出来了）

代码

#include<iostream>

#include<cstdio>

#include<cstdlib>

#include<cstring>

#include<algorithm>

#include<vector>

using namespace std;

const int maxN=10011;

const int inf=2147483647;

int n;

int root;

vector<int> E[maxN];

int Parent[maxN][25];

int Depth[maxN];

bool vis[maxN];

int read();//读入优化

void LCA_init();

void dfs(int u);

int LCA(int a,int b);

int main()

{

    int TT;

    TT=read();

    for (int ti=1;ti<=TT;ti++)

    {

        n=read();

        for (int i=1;i<=n;i++)

            E[i].clear();

        memset(vis,0,sizeof(vis));

        for (int i=1;i<n;i++)

        {

            int x=read(),y=read();

            E[x].push_back(y);

            vis[y]=1;

        }

        for (int i=1;i<=n;i++)

            if (vis[i]==0)

                root=i;

        //cout<<root<<endl;

        LCA_init();//LCA的初始化，即计算Depth和Parent数组

        cout<<LCA(read(),read())<<endl;

    }

    return 0;

}

int read()

{

    int x=0;

    int k=1;

    char ch=getchar();

    while (((ch>'9')||(ch<'0'))&&(ch!='-'))

        ch=getchar();

    if (ch=='-')

    {

        k=-1;

        ch=getchar();

    }

    while ((ch<='9')&&(ch>='0'))

    {

        x=x*10+ch-48;

        ch=getchar();

    }

    return x*k;

}

void LCA_init()

{

    memset(Depth,0,sizeof(Depth));

    Depth[root]=0;

    memset(Parent,0,sizeof(Parent));

    dfs(root);//首先用dfs计算出Depth和Parent[u][0]

    int kk=0;

    for (int j=1;j<=20;j++)//注意这里必须是j的循环在外面，i在里面，这是为了保证要计算某个值时它所需要的值已经计算出来了。

        for (int i=1;i<=n;i++)

            Parent[i][j]=Parent[Parent[i][j-1]][j-1];

    /*for (int i=1;i<=n;i++)

    {

        for (int j=0;j<=kk;j++)

            cout<<Parent[i][j]<<' ';

        cout<<endl;

    }

    */

}

void dfs(int u)

{

    for (int i=0;i<E[u].size();i++)

    {

        int v=E[u][i];

        Depth[v]=Depth[u]+1;

        Parent[v][0]=u;

        dfs(v);

    }

    return;

}

int LCA(int a,int b)

{

    if (Depth[b]>Depth[a])//保证a的深度>=b的深度

        swap(a,b);

    for (int i=20;i>=0;i--)//把a提到与b高度一致

        if ((Parent[a][i]!=0)&&(Depth[Parent[a][i]]>=Depth[b]))

            a=Parent[a][i];

    if (a==b)

        return a;

    for (int i=20;i>=0;i--)//把a和b同时向上提

        if ((Parent[a][i]!=0)&&(Parent[b][i]!=0)&&(Parent[a][i]!=Parent[b][i]))

        {

            a=Parent[a][i];

            b=Parent[b][i];

        }

    return Parent[a][0];注意返回值

}